人教版数学六年级上册 期末总复习课件(87张ppt)
文档属性
| 名称 | 人教版数学六年级上册 期末总复习课件(87张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览









文档简介
(共87张PPT)
小学数学六年级上册
位置与方向(二)
分数乘、除法
圆
百分数
扇形统计图
数学广角--数与形
知识点
比的意义和基本性质
第一阶段
一、计算
小刚 小时走了 千米 ,他1小时走多少千米?
15
14
10
3
3
2
计算
二、快速找出“1”的量:
1:女生人数是男生人数的 。
2:已完成的占总数的 。
3:剩下的比用去的多 。
4:我们班学习自觉的同学占全班人数的 。
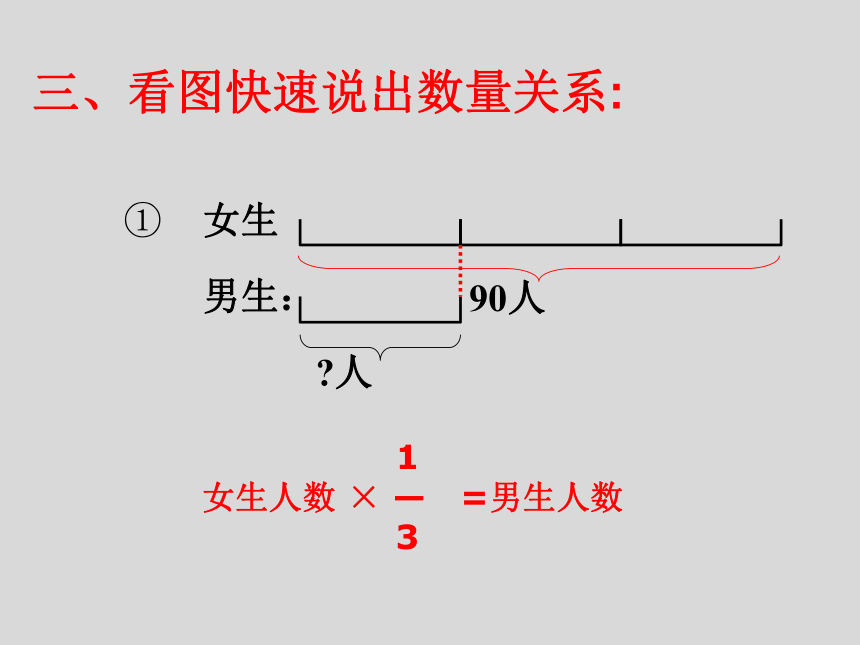
90人
人
女生
男生:
三、看图快速说出数量关系:
①
1
女生人数 × — =男生人数
3
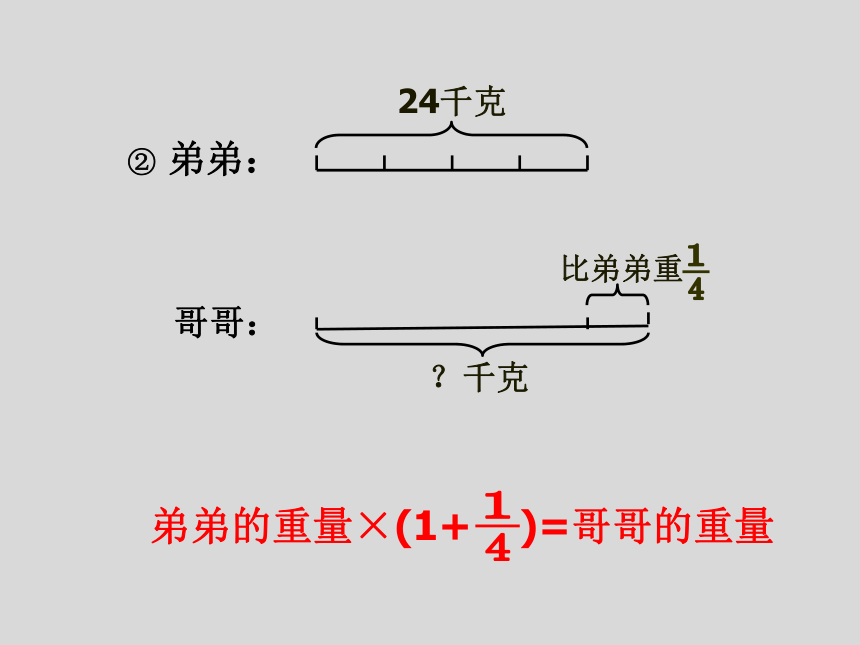
② 弟弟:
哥哥:
?千克
24千克
比弟弟重
弟弟的重量×(1+ )=哥哥的重量
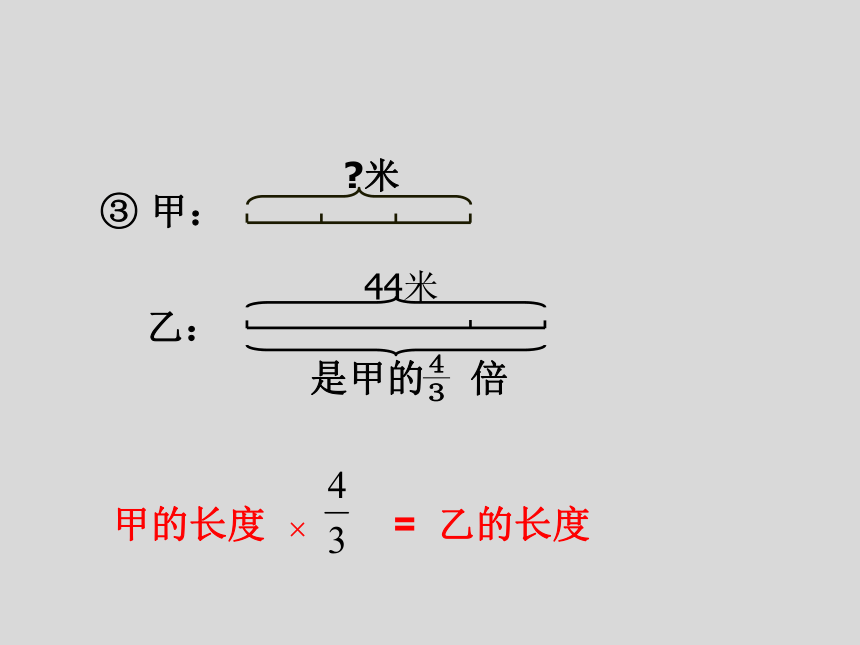
③ 甲:
乙:
是甲的 倍
米
44米
甲的长度 × = 乙的长度
四、对比理解
1、校园里有桂花树90棵,香樟树是桂花树的 ,香樟树有多少棵?
2、校园里有香樟树30棵,香樟树是桂花树的 ,桂花树有多少棵?
桂花树的棵数×1/3=香樟树的棵数
香樟树的棵数÷1/3=桂花树的棵数
3、校园里有桂花树90棵,香樟树比桂花树少 ,香樟树有多少棵?
4、校园里有香樟树30棵,香樟树比桂花树少 ,桂花树有多少棵?
对比理解
桂花树的棵数×(1-2/3)=香樟树的棵数
香樟树棵数÷(1-2/3)=桂花树的棵数
②甲、乙、丙三个书架,乙书架有180本书,甲书架上的书是乙书架的 ,又是丙书架的 ,丙书架有多少本?
1 2
180× — ÷ — =90(本)
3 3
1.求一个数是另一个数的几分之几,用除法。
2.求一个数的几分之几是多少,用乘法。
3.已知一个数的几分之几是多少,求这个数,可用除法也可以解方程。
解题关键:
抓住含有分率的句子,确定题的类型,从而选择正确的方法。
第二阶段
除法
分数
比
倒数
比的基本性质
化简比
可以用 15÷10 表示长是宽的多少倍
也可以用 10÷15 表示宽是长的几分之几
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10
宽和长的比是10比15
比的意义
两数相除又叫做两个数的比.
化简比
化简整数比:化成分数形式再约分
化简分数比:化成分数除法计算后改写成比的形式
化简小数比:把比的前项、后项都乘10、100、… 化成整数再化简
12:18
1.8:0.09
比的各部分名称是什么
前项 比号 后项
什么是比值 怎样求比值
比的前项除以后项所得的商叫做比值。 比值可以怎样表示
一般写成分数、整数或小数。
比的意义
1、求比值:
1.5∶2.5
2.8∶ ∶
2、填空
3∶( )=24 ( )∶8=0.5
3
︰
2
前项
后项
比号
=
3
÷
2
=
比值
3
2
比的读写:
如何去求一个比的比值呢
前项÷后项
比和除法、分数的关系
除法中的除数 和分数中的分母 不能为 0,那么比的后项呢?
除法中的除数 和分数中的分母 不能为 0,比的后项也不能为0。
你还记得商不变的性质吗?
你还记得分数的基本性质吗?
什么是比的基本性质?
比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
小明的身高1米,他爸爸的身高是173厘米,小明说他和他爸爸的身高比是1 :173,对不对?
如果不对,你认为是多少呢?
100︰ 173
1︰ 1.73
10︰ 17.3
一试身手
1、红花和黄花共70朵,红花与黄花的比
是2:5,求红花与黄花各是多少朵?
2、红花比黄花多20朵,红花与黄花的比
是7:3,求红花与黄花各是多少朵?
3、红花有28朵,红花与黄花的比是
4:7,求黄花有多少朵?
按比例分配:
第三阶段
邮递员小王每天从邮局“O”骑车出发,把报纸送到A,B,C,D,E,F6位订户家中。
(2) 小王每天把报纸送到 6 位订户家中,往返最少要行
路。
(1)请你分别表示出各订户的位置:
A(2,1)、B(4,2)、C(5,4)、D(6,5)、E(6,3)、F(6,0)
(2200m)
想一想:用数对怎么表示物体的位置?
用数对表示物体的位置,要先确定列数,再确定行数。)(竖为列,横为行。例:2列3行表示为(2,3))
0
1
2
3
4
5
6
1
2
3
4
5
6
动物园示意图
●
●
●
●
●
大象馆
猴山
熊猫馆
大门
海洋馆
⑴我用(3,0)表示大门的位置,你能表示其他场馆所在位置吗?
(1,4)
大象馆
猴山
熊猫馆
(2,2)
(3,5)
海洋馆
(6,4)
⑵在图上标出下面场馆的位置。
飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3)
●
●
●
飞禽馆
猩猩馆
狮虎山
例题2
⑵描出下列各点并依次连成封闭图形,看看是什么图形。A(5,9)B(2,1)C(9,6)D(1,6)E(8,1)
B
C
D
E
●
●
●
●
第四阶段
O
r
d
圆的周长指的是什么?
r
d
C=πd
C=2πr
围成圆的曲线的长叫做圆的周长。
一个女孩推着一个半径是35㎝的车轮在地面上滚动20周,车轮所走的路程是多少米?
=2×3.14×20
=125.6(米)
答:车轮所走过的路程是125.6米。
圆的面积指的又是什么?
r
圆所占平面的大小叫做圆的面积。
S=πr
知道什么条件可以求圆的面积?
一头小牛被一条长5米的绳子拴在一根木桩上,它的最大活动范围是多少平方米?
=3.14×5×5
=31.4(平方米)
答:它的最大活动范围是31.4平方米
这是什么图形?
又如何求它的面积呢?
S=π(R -r )
r
R
一个圆形花坛,它的直径是8米,现在它的周围修筑一条宽是1米的环形小路。这条小路的面积是多少平方米?
s=π(R -r )
=3.14×[(d/2+1) -(d/2) ]
=3.14×[(8/2+1) -(8/2) ]
=3.14×[5 -4 ]
=3.14×9
=28.26(平方米)
答:这条小路的面积是28.26平方米。
圆的周长:
圆的面积:
1、计算运动场的周长和面积。
1、求阴影部分的面积。
第五阶段
表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
分数
表示两个数量之间的倍数关系,也可表示某个具体数量
百分数
只表示两个数量之间的倍数关系
中国耕地面积占世界耕地总面积的
7%,而人口占世界总人口的22%。
中国十五期间保持 的经济增速。
100
7
一根光缆长 米。
100
81
(1)图中阴影部分占
整个图形的几分之几?
用百分数怎样表示?
(2)图中空白部分占阴影部分的几分之几?
用百分数怎样表示?
找准单位“1”
分数 百分数 小数 的互化
把分数化成百分数:
通常先把分数化成小数(除不尽时,通常保留三数),再把小数化成百分数;把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
40%
3%
12.5%
1
25
3
4
1
5
=
2
5
=
3
100
=
1
8
=75%
=4%
=20%
百分数
改写成分母是100的分数,能约分的要约分
通常先化成小数,再化成百分数
分数
分数与百分数互化
小数与分数互化
0.4
0.03
0.125
1
25
3
4
1
5
=
2
5
=
3
100
=
1
8
=0.75
=0.04
=0.2
先化成分母是10、100、1000的分数,再约分
用分子除以分母
小数
分数
0.15
0.429
1.23
72%
17.5%
200%
=15%
=42.9%
=123%
=0.72
=0.175
=2
小数点向右移动两位,添上%
小数点向左移动两位,去掉%
小数
百分数
小数与百分数互化
小数
分数
先化成分母是10、100、1000……的分数,再约分。
分子÷分母,除不尽时四舍五入
百分数
小数点向右移动两位,后面加上“%”
去掉“%”,小数点向左移动两位
先把百分数改写成分母是100的分数,约分成最简分数。
先把分数化成小数(除不尽时,通常保留三位小数),
再把小数化成百分数。
找单位“1”
(1).甲的 是乙。
6
7
(2).乙是甲的 。
4
5
(3).乙的 26% 相当于甲。
(4).宽是长的 80% 。
看谁先找到题中的单位“1”。
(1)小牛头数的大牛的 。
5
6
(2)计划产量是实际的 。
9
10
(3)女生人数的 相当于男生。
3
4
(4)鹅的只数是鸭的 。
2
5
(1)池塘里有12只鸭和4只鹅,鹅的只数是鸭的几分之几?
(2)池塘里有12只鸭,鹅的只数是鸭的 。池塘里有多少只鹅?
1
3
1
3
(3)池塘里有4只鹅,正好是鸭的只数的 。池塘里有多少只鸭?
先分析数量关系,再解答。
(1)池塘里有12只鸭和4只鹅,
鹅的只数是鸭的几分之几?
鸭:
鹅:
12只
4只
单位“1”
求一个数是另一个数的几分之几(或几倍)是多少,用除法计算。
4÷12=
1
3
答:鹅的只数是鸭的 。
1
3
鸭:
鹅:
12只
?只
求一个数的几分之几 是多少,用乘法计算。
12× =4(只)
1
3
答:池塘里有4只鹅。
(2)池塘里有12只鸭,鹅的只数是鸭的 。池塘里有多少只鹅?
1
3
单位“1”
鸭:
鹅:
?只
4只
单位“1”
单位“1”的量未知,
可直接用除法计算。
4÷ =12(只)
1
3
答:池塘里有12只鸭。
1
3
× =
鸭的只数
鹅
1
3
(3)池塘里有4只鹅,正好是鸭的只数的 。池塘里有多少只鸭?
C
种一批树,活了100棵,死了1棵,求成活率的正确算式是( )。
A:
100-1
100
×100%
B:
100-1
100+1
×100%
C:
100
100+1
×100%
某县种子推广站,用300粒玉米种子作发芽试验,结果发芽的种子有288粒。求发芽率。
=0.96×100%
=96%
发芽率= ×100%
288
300
发芽率=
发芽种子数
试验种子总数
×100%
1. 六年级有学生160人,已达到《国家体育锻炼标准》(儿童组)的有120人,
占六年级人数的百分之几?
120÷160=0.75=75%
答:占六年级的学生人数的75%。
一个数是另一个数的百分之几
(百分率)
2.李平家用600千克稻谷碾出420千克大米,他家稻谷的出米率是多少?
稻谷的出米率 =
大米的重量
稻谷的重量
×100%
=
420
600
×100%
=
70%
答:他家稻谷的出米率是70%。
一个盐场用160吨海水制出4800千克盐。这种海水的含盐率是多少?
注意审题:
→最多能达到100%
→达不到100%
→最多能达到100%
→最多能达到100%
→最多能达到100%
常见的百分率
→能超过100%
→最多能达到100%
→最多能达到100%
→达不到100%
→达不到100%
常见的百分率
解题三步骤:
1.求出多或者少的具体量
2.除以单位1(除数)
3.化成百分数(×100%)
求一个数比另一个数多(少)百分之几
1、找单位1
2、判断乘除(已知×未知÷)
3、判断加减
百分数乘除法解决问题三步骤:
王叔叔家六月份用电量是120度(千瓦.时),七月份比六月份节约了20%。王叔叔家七月份用电量是多少度?
单位“1”: 六月份的用电量 (已知量)
120×(1-20%)
=120×80%
=120×0.8
=96(度)
答:王叔叔家七月份用电量是96度。
1、某科技城一张光盘原价4元,现价2.5元,现价比原价便宜了百分之几?
2、商场上个月的营业额是30万元,这个月的营业额下降了6%,这个月的营业额是多少万元?
1.(4-2.5)÷4 ×100%
=1.5 ÷4 ×100%
=0.375 ×100%
=37.5%
答:现价比原价便宜了37.5%。
2、 30×(1-6%)
=30 ×94%
=30 ×0.94
=28.2(万元)
答:这个月的营业额是28.2万元。
巩固练习
3、 小强家的鸡舍占地面积是16㎡,翻建后占地20㎡,现在鸡舍的占地面积比原来增长了百分之几?
4、小丽去年的身高是125cm,今年的身高133cm,小丽今年的身高比去年增加了百分之几?
3、(20-16)÷16 ×100%
=4 ÷ 16×100%
=0.25 ×100%
=25%
答:现在鸡舍的占地面积比原来增加了25%。
4、(133-125)÷125 ×100%
=8 ÷ 125×100%
=0.064 ×100%
=6.4%
答:小丽今年的身高比去年增加了6.4%。
巩固练习
对比练习
1. 松树有40棵,杨树有50棵。
(1)松树是杨树的几分之几?
(2)杨树是松树的几分之几?
(3)松树比杨树少几分之几?
(4)杨树比松树多几分之几?
1. 松树有40棵,杨树有50棵。
(5)松树是杨树的百分之几?
(6)杨树是松树的百分之几?
(7)松树比杨树少百分之几?
(8)杨树比松树多百分之几?
2.松树有40棵, ,杨树有多少棵?
2. 松树有40棵, ,杨树有多少棵?
3. 杨树有50棵, ,松树有多少棵?
巩固练习
4、甲数比乙数少20%,乙数就比甲数多( )%。
25
乙是单位1,即100%
甲比乙少20%,甲:100% - 20%=80%
甲:乙=80%:100%=80:100=4:5
(5—4) ÷4 ×100 %=25%
甲:4份,乙:5份
5.填空:
1、6÷24= =( ):( )
=( )=( )%=
( )
( )
( )
16
6
24
1
4
1 4
0.25
小数
25
4
6、把0.67、0.66、 、67%按从小到大的顺序排列。
________________________
2
3
˙
˙
0.66< <67%<0.67
˙
˙
2
3
7. 六年级参加植树活动,计划栽500棵松树,实际多栽了20%,实际多栽了几棵松树?
实际比计划多栽20%
500 ×20 % =100(棵)
8. 超市里今天的牛奶进货量是300袋,卖出了70%,还剩下几袋没有卖出?
还剩:1—70%=30%
300 × (1—70%)=90(袋)
9. 电视机厂生产了1000台电视机,经过检查,不合格的有15台,这批电视机的合格率是多少?
方法1:
合格的电视机:
1000—15=9985(台)
合格率:
9985 ÷ 1000=98.5%
方法2:
不合格率:
15 ÷ 1000=1.5%
合格率:
1-1.5%=98.5%
10.一堆煤用去20%,剩下的比用去的多12吨,这堆煤有多少吨?
方法1:列方程
解:设这堆煤有x吨,则剩下的为(1-20%)x吨.
(1-20%x)-20%x=12
60%x=12
x=12÷60%
x=20
方法2:算式
12 ÷(1-20%-20%)
=12 ÷60%
=20(吨)
方法3:比
用去:剩下=20%:(1-20%)
=20:80=1:4
12 ÷(4-1) ×(4+1)
=4 × 5
=20(吨)
第六阶段
摄入量/克
0
500
1000
1500
2000
油脂类
奶类和豆类
鱼、禽、肉、蛋
等
类
蔬菜和水果类
谷类
50
450
600
900
1800
种类
从条形统计图中能很清楚看出数量的多少。
如果要更清楚地了解各部分数量同总数之间的关系,可以用扇形统计图表示。
谷类47.4%
蔬菜和水果类23.7%
鱼、禽、肉、蛋等类15.8%
奶类和豆类11.8%
油脂类1.3%
扇形统计图是用整个圆表示( ),用圆内各个扇形的大小表示各部分数量占( )的( )。
总量
总量
百分比
某小学对全体学生进行了体重调查,体重正常的学生有319人。下图是调查结果统计图。
1、这个小学一共有多少人?
2、体重偏胖、偏瘦的各有多少人?
及格25%
( )人
良40%
优30%
不及格2人
右图是六(4)班体育成绩统计图,你能算出及格的人数吗?
小学数学六年级上册
位置与方向(二)
分数乘、除法
圆
百分数
扇形统计图
数学广角--数与形
知识点
比的意义和基本性质
第一阶段
一、计算
小刚 小时走了 千米 ,他1小时走多少千米?
15
14
10
3
3
2
计算
二、快速找出“1”的量:
1:女生人数是男生人数的 。
2:已完成的占总数的 。
3:剩下的比用去的多 。
4:我们班学习自觉的同学占全班人数的 。
90人
人
女生
男生:
三、看图快速说出数量关系:
①
1
女生人数 × — =男生人数
3
② 弟弟:
哥哥:
?千克
24千克
比弟弟重
弟弟的重量×(1+ )=哥哥的重量
③ 甲:
乙:
是甲的 倍
米
44米
甲的长度 × = 乙的长度
四、对比理解
1、校园里有桂花树90棵,香樟树是桂花树的 ,香樟树有多少棵?
2、校园里有香樟树30棵,香樟树是桂花树的 ,桂花树有多少棵?
桂花树的棵数×1/3=香樟树的棵数
香樟树的棵数÷1/3=桂花树的棵数
3、校园里有桂花树90棵,香樟树比桂花树少 ,香樟树有多少棵?
4、校园里有香樟树30棵,香樟树比桂花树少 ,桂花树有多少棵?
对比理解
桂花树的棵数×(1-2/3)=香樟树的棵数
香樟树棵数÷(1-2/3)=桂花树的棵数
②甲、乙、丙三个书架,乙书架有180本书,甲书架上的书是乙书架的 ,又是丙书架的 ,丙书架有多少本?
1 2
180× — ÷ — =90(本)
3 3
1.求一个数是另一个数的几分之几,用除法。
2.求一个数的几分之几是多少,用乘法。
3.已知一个数的几分之几是多少,求这个数,可用除法也可以解方程。
解题关键:
抓住含有分率的句子,确定题的类型,从而选择正确的方法。
第二阶段
除法
分数
比
倒数
比的基本性质
化简比
可以用 15÷10 表示长是宽的多少倍
也可以用 10÷15 表示宽是长的几分之几
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10
宽和长的比是10比15
比的意义
两数相除又叫做两个数的比.
化简比
化简整数比:化成分数形式再约分
化简分数比:化成分数除法计算后改写成比的形式
化简小数比:把比的前项、后项都乘10、100、… 化成整数再化简
12:18
1.8:0.09
比的各部分名称是什么
前项 比号 后项
什么是比值 怎样求比值
比的前项除以后项所得的商叫做比值。 比值可以怎样表示
一般写成分数、整数或小数。
比的意义
1、求比值:
1.5∶2.5
2.8∶ ∶
2、填空
3∶( )=24 ( )∶8=0.5
3
︰
2
前项
后项
比号
=
3
÷
2
=
比值
3
2
比的读写:
如何去求一个比的比值呢
前项÷后项
比和除法、分数的关系
除法中的除数 和分数中的分母 不能为 0,那么比的后项呢?
除法中的除数 和分数中的分母 不能为 0,比的后项也不能为0。
你还记得商不变的性质吗?
你还记得分数的基本性质吗?
什么是比的基本性质?
比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
小明的身高1米,他爸爸的身高是173厘米,小明说他和他爸爸的身高比是1 :173,对不对?
如果不对,你认为是多少呢?
100︰ 173
1︰ 1.73
10︰ 17.3
一试身手
1、红花和黄花共70朵,红花与黄花的比
是2:5,求红花与黄花各是多少朵?
2、红花比黄花多20朵,红花与黄花的比
是7:3,求红花与黄花各是多少朵?
3、红花有28朵,红花与黄花的比是
4:7,求黄花有多少朵?
按比例分配:
第三阶段
邮递员小王每天从邮局“O”骑车出发,把报纸送到A,B,C,D,E,F6位订户家中。
(2) 小王每天把报纸送到 6 位订户家中,往返最少要行
路。
(1)请你分别表示出各订户的位置:
A(2,1)、B(4,2)、C(5,4)、D(6,5)、E(6,3)、F(6,0)
(2200m)
想一想:用数对怎么表示物体的位置?
用数对表示物体的位置,要先确定列数,再确定行数。)(竖为列,横为行。例:2列3行表示为(2,3))
0
1
2
3
4
5
6
1
2
3
4
5
6
动物园示意图
●
●
●
●
●
大象馆
猴山
熊猫馆
大门
海洋馆
⑴我用(3,0)表示大门的位置,你能表示其他场馆所在位置吗?
(1,4)
大象馆
猴山
熊猫馆
(2,2)
(3,5)
海洋馆
(6,4)
⑵在图上标出下面场馆的位置。
飞禽馆(1,1) 猩猩馆(0,3) 狮虎山(4,3)
●
●
●
飞禽馆
猩猩馆
狮虎山
例题2
⑵描出下列各点并依次连成封闭图形,看看是什么图形。A(5,9)B(2,1)C(9,6)D(1,6)E(8,1)
B
C
D
E
●
●
●
●
第四阶段
O
r
d
圆的周长指的是什么?
r
d
C=πd
C=2πr
围成圆的曲线的长叫做圆的周长。
一个女孩推着一个半径是35㎝的车轮在地面上滚动20周,车轮所走的路程是多少米?
=2×3.14×20
=125.6(米)
答:车轮所走过的路程是125.6米。
圆的面积指的又是什么?
r
圆所占平面的大小叫做圆的面积。
S=πr
知道什么条件可以求圆的面积?
一头小牛被一条长5米的绳子拴在一根木桩上,它的最大活动范围是多少平方米?
=3.14×5×5
=31.4(平方米)
答:它的最大活动范围是31.4平方米
这是什么图形?
又如何求它的面积呢?
S=π(R -r )
r
R
一个圆形花坛,它的直径是8米,现在它的周围修筑一条宽是1米的环形小路。这条小路的面积是多少平方米?
s=π(R -r )
=3.14×[(d/2+1) -(d/2) ]
=3.14×[(8/2+1) -(8/2) ]
=3.14×[5 -4 ]
=3.14×9
=28.26(平方米)
答:这条小路的面积是28.26平方米。
圆的周长:
圆的面积:
1、计算运动场的周长和面积。
1、求阴影部分的面积。
第五阶段
表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
分数
表示两个数量之间的倍数关系,也可表示某个具体数量
百分数
只表示两个数量之间的倍数关系
中国耕地面积占世界耕地总面积的
7%,而人口占世界总人口的22%。
中国十五期间保持 的经济增速。
100
7
一根光缆长 米。
100
81
(1)图中阴影部分占
整个图形的几分之几?
用百分数怎样表示?
(2)图中空白部分占阴影部分的几分之几?
用百分数怎样表示?
找准单位“1”
分数 百分数 小数 的互化
把分数化成百分数:
通常先把分数化成小数(除不尽时,通常保留三数),再把小数化成百分数;把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
40%
3%
12.5%
1
25
3
4
1
5
=
2
5
=
3
100
=
1
8
=75%
=4%
=20%
百分数
改写成分母是100的分数,能约分的要约分
通常先化成小数,再化成百分数
分数
分数与百分数互化
小数与分数互化
0.4
0.03
0.125
1
25
3
4
1
5
=
2
5
=
3
100
=
1
8
=0.75
=0.04
=0.2
先化成分母是10、100、1000的分数,再约分
用分子除以分母
小数
分数
0.15
0.429
1.23
72%
17.5%
200%
=15%
=42.9%
=123%
=0.72
=0.175
=2
小数点向右移动两位,添上%
小数点向左移动两位,去掉%
小数
百分数
小数与百分数互化
小数
分数
先化成分母是10、100、1000……的分数,再约分。
分子÷分母,除不尽时四舍五入
百分数
小数点向右移动两位,后面加上“%”
去掉“%”,小数点向左移动两位
先把百分数改写成分母是100的分数,约分成最简分数。
先把分数化成小数(除不尽时,通常保留三位小数),
再把小数化成百分数。
找单位“1”
(1).甲的 是乙。
6
7
(2).乙是甲的 。
4
5
(3).乙的 26% 相当于甲。
(4).宽是长的 80% 。
看谁先找到题中的单位“1”。
(1)小牛头数的大牛的 。
5
6
(2)计划产量是实际的 。
9
10
(3)女生人数的 相当于男生。
3
4
(4)鹅的只数是鸭的 。
2
5
(1)池塘里有12只鸭和4只鹅,鹅的只数是鸭的几分之几?
(2)池塘里有12只鸭,鹅的只数是鸭的 。池塘里有多少只鹅?
1
3
1
3
(3)池塘里有4只鹅,正好是鸭的只数的 。池塘里有多少只鸭?
先分析数量关系,再解答。
(1)池塘里有12只鸭和4只鹅,
鹅的只数是鸭的几分之几?
鸭:
鹅:
12只
4只
单位“1”
求一个数是另一个数的几分之几(或几倍)是多少,用除法计算。
4÷12=
1
3
答:鹅的只数是鸭的 。
1
3
鸭:
鹅:
12只
?只
求一个数的几分之几 是多少,用乘法计算。
12× =4(只)
1
3
答:池塘里有4只鹅。
(2)池塘里有12只鸭,鹅的只数是鸭的 。池塘里有多少只鹅?
1
3
单位“1”
鸭:
鹅:
?只
4只
单位“1”
单位“1”的量未知,
可直接用除法计算。
4÷ =12(只)
1
3
答:池塘里有12只鸭。
1
3
× =
鸭的只数
鹅
1
3
(3)池塘里有4只鹅,正好是鸭的只数的 。池塘里有多少只鸭?
C
种一批树,活了100棵,死了1棵,求成活率的正确算式是( )。
A:
100-1
100
×100%
B:
100-1
100+1
×100%
C:
100
100+1
×100%
某县种子推广站,用300粒玉米种子作发芽试验,结果发芽的种子有288粒。求发芽率。
=0.96×100%
=96%
发芽率= ×100%
288
300
发芽率=
发芽种子数
试验种子总数
×100%
1. 六年级有学生160人,已达到《国家体育锻炼标准》(儿童组)的有120人,
占六年级人数的百分之几?
120÷160=0.75=75%
答:占六年级的学生人数的75%。
一个数是另一个数的百分之几
(百分率)
2.李平家用600千克稻谷碾出420千克大米,他家稻谷的出米率是多少?
稻谷的出米率 =
大米的重量
稻谷的重量
×100%
=
420
600
×100%
=
70%
答:他家稻谷的出米率是70%。
一个盐场用160吨海水制出4800千克盐。这种海水的含盐率是多少?
注意审题:
→最多能达到100%
→达不到100%
→最多能达到100%
→最多能达到100%
→最多能达到100%
常见的百分率
→能超过100%
→最多能达到100%
→最多能达到100%
→达不到100%
→达不到100%
常见的百分率
解题三步骤:
1.求出多或者少的具体量
2.除以单位1(除数)
3.化成百分数(×100%)
求一个数比另一个数多(少)百分之几
1、找单位1
2、判断乘除(已知×未知÷)
3、判断加减
百分数乘除法解决问题三步骤:
王叔叔家六月份用电量是120度(千瓦.时),七月份比六月份节约了20%。王叔叔家七月份用电量是多少度?
单位“1”: 六月份的用电量 (已知量)
120×(1-20%)
=120×80%
=120×0.8
=96(度)
答:王叔叔家七月份用电量是96度。
1、某科技城一张光盘原价4元,现价2.5元,现价比原价便宜了百分之几?
2、商场上个月的营业额是30万元,这个月的营业额下降了6%,这个月的营业额是多少万元?
1.(4-2.5)÷4 ×100%
=1.5 ÷4 ×100%
=0.375 ×100%
=37.5%
答:现价比原价便宜了37.5%。
2、 30×(1-6%)
=30 ×94%
=30 ×0.94
=28.2(万元)
答:这个月的营业额是28.2万元。
巩固练习
3、 小强家的鸡舍占地面积是16㎡,翻建后占地20㎡,现在鸡舍的占地面积比原来增长了百分之几?
4、小丽去年的身高是125cm,今年的身高133cm,小丽今年的身高比去年增加了百分之几?
3、(20-16)÷16 ×100%
=4 ÷ 16×100%
=0.25 ×100%
=25%
答:现在鸡舍的占地面积比原来增加了25%。
4、(133-125)÷125 ×100%
=8 ÷ 125×100%
=0.064 ×100%
=6.4%
答:小丽今年的身高比去年增加了6.4%。
巩固练习
对比练习
1. 松树有40棵,杨树有50棵。
(1)松树是杨树的几分之几?
(2)杨树是松树的几分之几?
(3)松树比杨树少几分之几?
(4)杨树比松树多几分之几?
1. 松树有40棵,杨树有50棵。
(5)松树是杨树的百分之几?
(6)杨树是松树的百分之几?
(7)松树比杨树少百分之几?
(8)杨树比松树多百分之几?
2.松树有40棵, ,杨树有多少棵?
2. 松树有40棵, ,杨树有多少棵?
3. 杨树有50棵, ,松树有多少棵?
巩固练习
4、甲数比乙数少20%,乙数就比甲数多( )%。
25
乙是单位1,即100%
甲比乙少20%,甲:100% - 20%=80%
甲:乙=80%:100%=80:100=4:5
(5—4) ÷4 ×100 %=25%
甲:4份,乙:5份
5.填空:
1、6÷24= =( ):( )
=( )=( )%=
( )
( )
( )
16
6
24
1
4
1 4
0.25
小数
25
4
6、把0.67、0.66、 、67%按从小到大的顺序排列。
________________________
2
3
˙
˙
0.66< <67%<0.67
˙
˙
2
3
7. 六年级参加植树活动,计划栽500棵松树,实际多栽了20%,实际多栽了几棵松树?
实际比计划多栽20%
500 ×20 % =100(棵)
8. 超市里今天的牛奶进货量是300袋,卖出了70%,还剩下几袋没有卖出?
还剩:1—70%=30%
300 × (1—70%)=90(袋)
9. 电视机厂生产了1000台电视机,经过检查,不合格的有15台,这批电视机的合格率是多少?
方法1:
合格的电视机:
1000—15=9985(台)
合格率:
9985 ÷ 1000=98.5%
方法2:
不合格率:
15 ÷ 1000=1.5%
合格率:
1-1.5%=98.5%
10.一堆煤用去20%,剩下的比用去的多12吨,这堆煤有多少吨?
方法1:列方程
解:设这堆煤有x吨,则剩下的为(1-20%)x吨.
(1-20%x)-20%x=12
60%x=12
x=12÷60%
x=20
方法2:算式
12 ÷(1-20%-20%)
=12 ÷60%
=20(吨)
方法3:比
用去:剩下=20%:(1-20%)
=20:80=1:4
12 ÷(4-1) ×(4+1)
=4 × 5
=20(吨)
第六阶段
摄入量/克
0
500
1000
1500
2000
油脂类
奶类和豆类
鱼、禽、肉、蛋
等
类
蔬菜和水果类
谷类
50
450
600
900
1800
种类
从条形统计图中能很清楚看出数量的多少。
如果要更清楚地了解各部分数量同总数之间的关系,可以用扇形统计图表示。
谷类47.4%
蔬菜和水果类23.7%
鱼、禽、肉、蛋等类15.8%
奶类和豆类11.8%
油脂类1.3%
扇形统计图是用整个圆表示( ),用圆内各个扇形的大小表示各部分数量占( )的( )。
总量
总量
百分比
某小学对全体学生进行了体重调查,体重正常的学生有319人。下图是调查结果统计图。
1、这个小学一共有多少人?
2、体重偏胖、偏瘦的各有多少人?
及格25%
( )人
良40%
优30%
不及格2人
右图是六(4)班体育成绩统计图,你能算出及格的人数吗?
