人教版数学六年级上册 第8单元 数学广角——数与形 课件(16张ppt)
文档属性
| 名称 | 人教版数学六年级上册 第8单元 数学广角——数与形 课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览



文档简介
第二课时
几何代数统一体,永远联系莫分离。
数与形,
本是相倚依,
焉能分做两边飞。
数缺形时少直观,形缺数时难入微。
数形结合百般好,隔离分家万事休。
切莫忘,
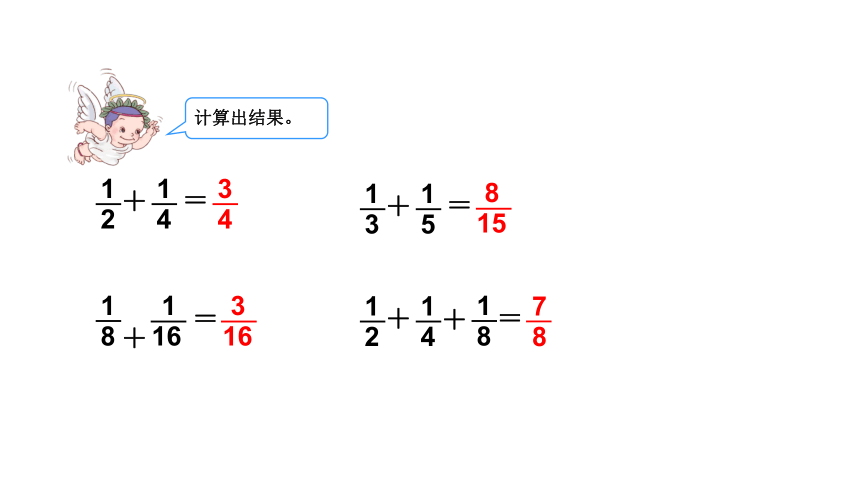
8
15
1
2
+
1
4
=
3
4
1
3
+
1
5
=
1
16
1
8
+
=
3
16
7
8
1
2
+
1
4
=
1
8
+
计算出结果。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
你能发现什么规律?
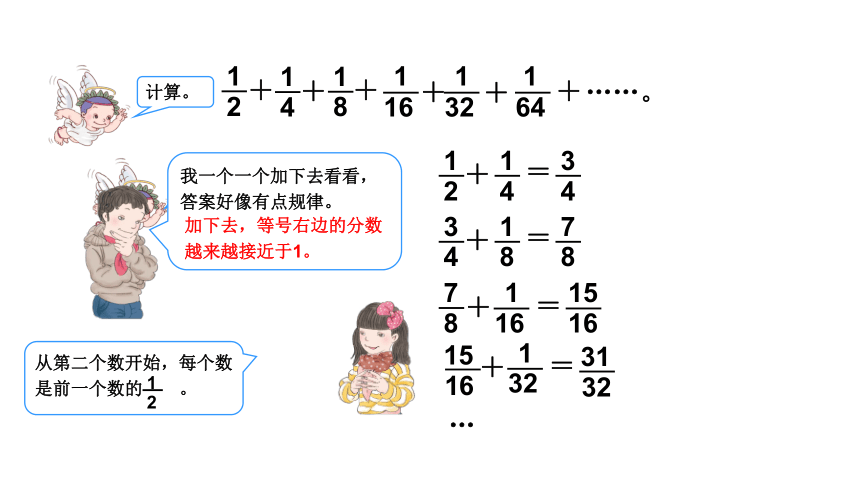
从第二个数开始,每个数是前一个数的 。
2
1
我一个一个加下去看看,
答案好像有点规律。
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
31
32
15
16
…
加下去,等号右边的分数
越来越接近于1。
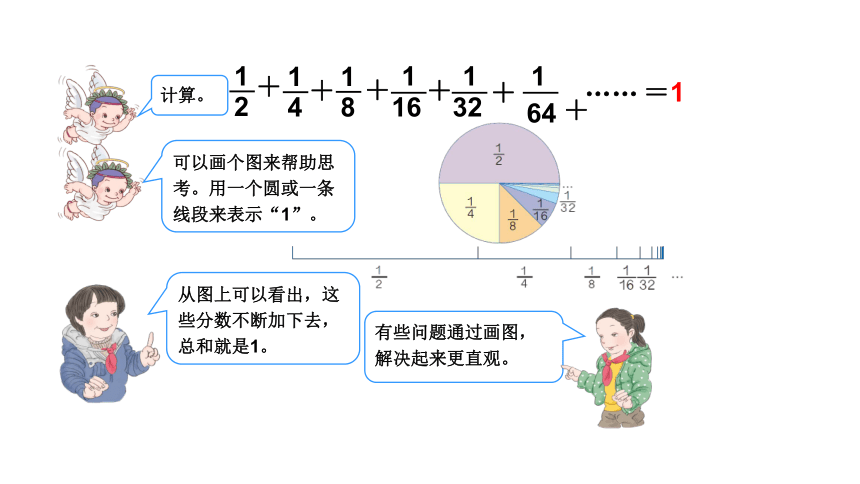
计算。
可以画个图来帮助思考。用一个圆或一条线段来表示“1”。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
…
=1
…
有些问题通过画图,解决起来更直观。
从图上可以看出,这些分数不断加下去,总和就是1。
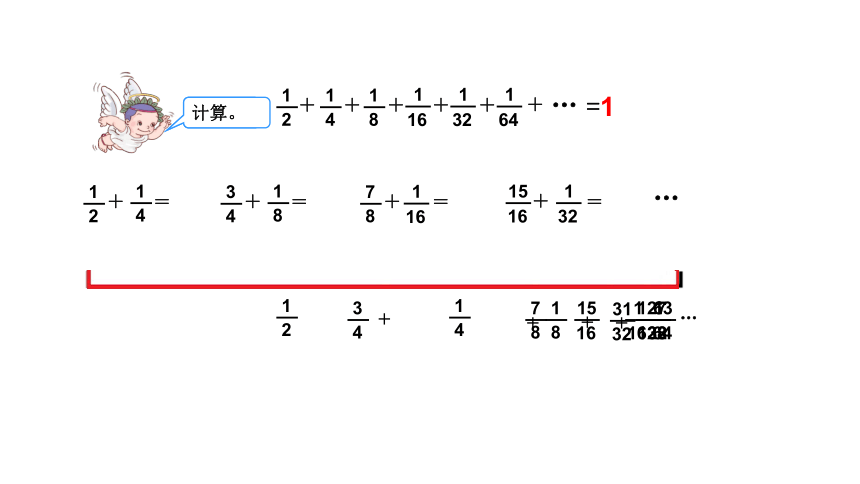
计算。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
=1
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
15
16
…
31
32
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
计算。
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
……。
=1
…
…
计算。
计算。
狗的速度是人的速度的2倍
200×2=400(米)
答:小狗从出发开始,一共跑了400米。
1. 一条马路长200 m,小亮和他的小狗分别以均匀的速度同时从马路的
起点出发。当小亮走到这条马路一半的时候,小狗已经到达马路的终
点。然后小狗返回与小亮相向而行,遇到小亮以后再跑向终点,到达
终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,
一共跑了多少米?
起点
终点
2. 你能用所学知识解决下列问题吗?
1
我是这样想的:
2
3
+
=
2
9
8
9
8
9
+
=
27
2
27
26
81
2
27
26
+
=
81
80
……
2
3
2
27
2
9
2
81
…
+
+
+
+
=
所以原式的结果是1。
答:小刚一共下了2盘,分别和小林、小强。
小刚
小林
小强
小芳
小兵
2
4
3
1
2
3. 小林、小强、小芳、小兵和小刚5 人进行象棋 比
赛,每2 人之间都要下一盘。小林已经下了4盘,
小强下了3盘,小芳下了2 盘,小兵下了1 盘。请
问:小刚一共下了几盘?分别和谁下的?
用连线的方法试试。
有着367种证明方式的勾股定理
a
b
c
毕达哥拉斯
古希腊
100以内数的认识
十 位
个 位
36是由 (3 )个十和(6) 个一组成的。
(
)
3
6
2
1
4
3
×
=
8
3
关于分数的学习:
75棵
杨树:
柳树:
比杨树多
5
4
?棵
柳树的棵树=杨树+柳树比杨树多的棵数
解决问题中画线段图表示数量关系
几何代数统一体,永远联系莫分离。
数与形,
本是相倚依,
焉能分做两边飞。
数缺形时少直观,形缺数时难入微。
数形结合百般好,隔离分家万事休。
切莫忘,
8
15
1
2
+
1
4
=
3
4
1
3
+
1
5
=
1
16
1
8
+
=
3
16
7
8
1
2
+
1
4
=
1
8
+
计算出结果。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
你能发现什么规律?
从第二个数开始,每个数是前一个数的 。
2
1
我一个一个加下去看看,
答案好像有点规律。
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
31
32
15
16
…
加下去,等号右边的分数
越来越接近于1。
计算。
可以画个图来帮助思考。用一个圆或一条线段来表示“1”。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
…
=1
…
有些问题通过画图,解决起来更直观。
从图上可以看出,这些分数不断加下去,总和就是1。
计算。
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
=1
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
15
16
…
31
32
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
计算。
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
……。
=1
…
…
计算。
计算。
狗的速度是人的速度的2倍
200×2=400(米)
答:小狗从出发开始,一共跑了400米。
1. 一条马路长200 m,小亮和他的小狗分别以均匀的速度同时从马路的
起点出发。当小亮走到这条马路一半的时候,小狗已经到达马路的终
点。然后小狗返回与小亮相向而行,遇到小亮以后再跑向终点,到达
终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,
一共跑了多少米?
起点
终点
2. 你能用所学知识解决下列问题吗?
1
我是这样想的:
2
3
+
=
2
9
8
9
8
9
+
=
27
2
27
26
81
2
27
26
+
=
81
80
……
2
3
2
27
2
9
2
81
…
+
+
+
+
=
所以原式的结果是1。
答:小刚一共下了2盘,分别和小林、小强。
小刚
小林
小强
小芳
小兵
2
4
3
1
2
3. 小林、小强、小芳、小兵和小刚5 人进行象棋 比
赛,每2 人之间都要下一盘。小林已经下了4盘,
小强下了3盘,小芳下了2 盘,小兵下了1 盘。请
问:小刚一共下了几盘?分别和谁下的?
用连线的方法试试。
有着367种证明方式的勾股定理
a
b
c
毕达哥拉斯
古希腊
100以内数的认识
十 位
个 位
36是由 (3 )个十和(6) 个一组成的。
(
)
3
6
2
1
4
3
×
=
8
3
关于分数的学习:
75棵
杨树:
柳树:
比杨树多
5
4
?棵
柳树的棵树=杨树+柳树比杨树多的棵数
解决问题中画线段图表示数量关系
