第30章 二次函数 单元测试卷(含解析)
文档属性
| 名称 | 第30章 二次函数 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览



文档简介
冀教版九年级数学下册第30章二次函数单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数属于二次函数的是 ( )
A.y=2x+1 B.y=(x-1)2-x2 C.y=2x2-7 D.y=-1x2
2.二次函数y=ax2+bx+c(a≠0)图像上部分点的坐标(x,y)对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图像的对称轴是 ( )
A.直线x=-3 B.直线x=-2 C.直线x=-1 D.直线x=0
3.若二次函数y=ax2-3x+7-5x2的图像有最低点,则a的值可以是 ( )
A.0 B.2 C.4 D.6
4.对于二次函数y=-14x2+x-4,下列说法正确的是 ( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图像的顶点坐标为(-2,-7) D.图像与x轴有两个交点
5.将二次函数y=x2+bx+c的图像先向右平移2个单位长度,再向下平移3个单位长度,所得图像的函数表达式为y=(x-1)2-4,则b,c的值分别为 ( )
A.2,0 B.2,-6 C.-6,8 D.-6,2
6.下列是抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图像的是 ( )
7.已知抛物线y=x2-(2m-1)x+2m不经过第三象限,且当x>2时,y随x的增大而增大,则实数m的取值范围是 ( )
A.0≤m≤2.5 B.m≥1.5 C.0≤m≤1.5 D.0 8.生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y与月份n之间的函数关系式为y=-n2+14n-24,则该企业一年中应停产的月份是 ( )
A.1月、2月、3月 B.2月、3月、4月 C.1月、2月、12月 D.1月、11月、12月
9.如图,正方形ABCD的边长为1,E,F,G,H分别为各边上的点,且AE=BF=CG=DH,设AE为x,小正方形EFGH的面积为y,则y关于x的函数对应的图像大致是 ( )
10.如图,一次函数y=-x与二次函数y=ax2+bx+c的图像相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上结论都正确
第10题图 第11题图
11.如图,排球运动员站在O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-h)2+k.已知球与O点的水平距离为6m时,球运行的高度达到最高2.6m,球网BC的高度为2.43m,与O点的水平距离为9m.球场的边界距O点的水平距离为18m,则下列判断正确的是 ( )
A.球不会过球网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
12.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为 ( )
A.-74 B.3或-3 C.2或-3 D.2或-3或-74
二、填空题(本大题共4小题,每小题3分,共12分)
13.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)?
14.如图,铅球被小明从手中抛出,铅球距地面的高度h(m)与抛出时间t(s)之间满足函数关系h=at2+1.6t,已知铅球被抛出后经过4s落地,则铅球距地面的最大高度是 m.?
15.四位同学在研究二次函数y=ax2+bx+c(a,b,c是常数,a≠0)时,甲发现当x=-1时,函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是 .?
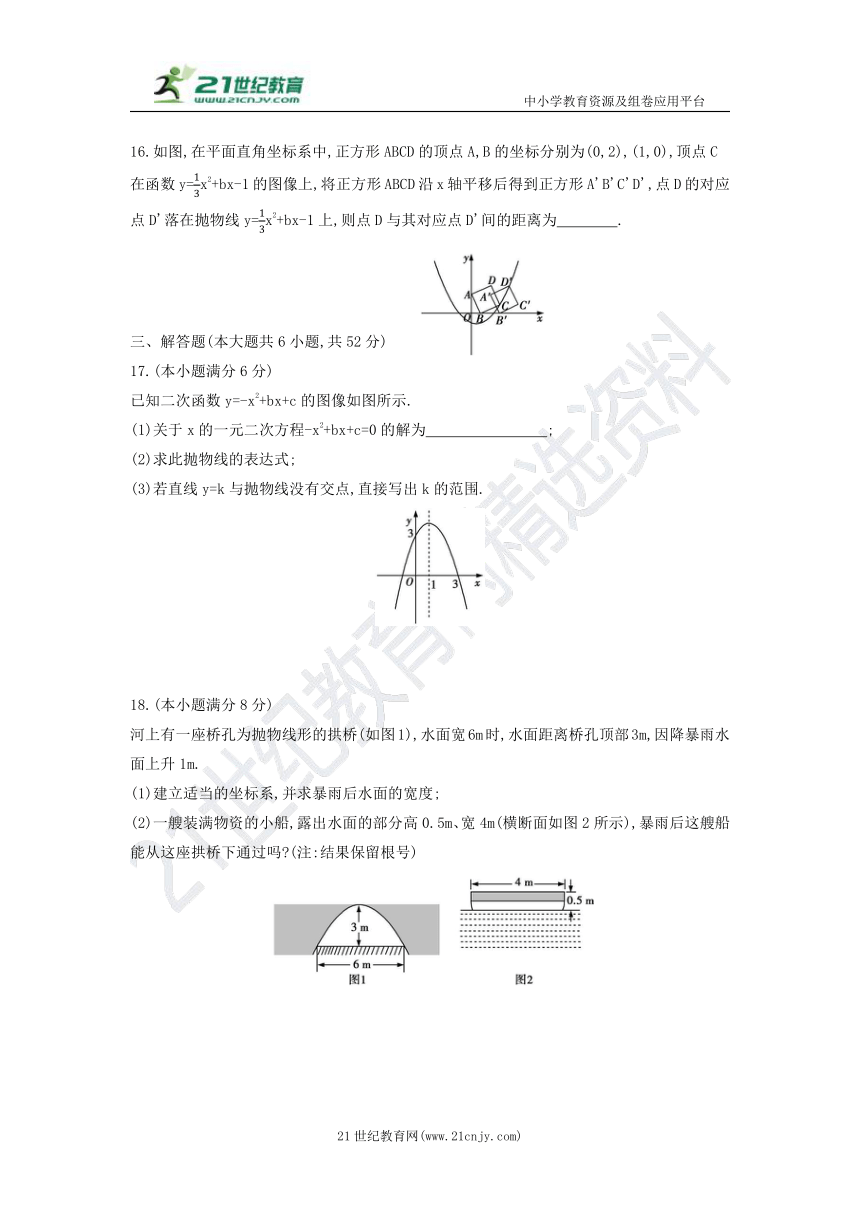
25317459550400016.如图,在平面直角坐标系中,正方形ABCD的顶点A,B的坐标分别为(0,2),(1,0),顶点C在函数y=13x2+bx-1的图像上,将正方形ABCD沿x轴平移后得到正方形A'B'C'D',点D的对应点D'落在抛物线y=13x2+bx-1上,则点D与其对应点D'间的距离为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分6分)
已知二次函数y=-x2+bx+c的图像如图所示.
(1)关于x的一元二次方程-x2+bx+c=0的解为 ;?
(2)求此抛物线的表达式;
(3)若直线y=k与抛物线没有交点,直接写出k的范围.
18.(本小题满分8分)
河上有一座桥孔为抛物线形的拱桥(如图1),水面宽6m时,水面距离桥孔顶部3m,因降暴雨水面上升1m.
(1)建立适当的坐标系,并求暴雨后水面的宽度;
(2)一艘装满物资的小船,露出水面的部分高0.5m、宽4m(横断面如图2所示),暴雨后这艘船能从这座拱桥下通过吗?(注:结果保留根号)
19.(本小题满分8分)
如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值.
20.(本小题满分8分)
在平面直角坐标系xOy中,已知抛物线y=x2-mx+n.
(1)当m=2时,
①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(-2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是 .?
(2)已知点P(-1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,抛物线与线段PQ恰有一个交点,结合函数图像,求m的取值范围.
21.(本小题满分10分)
某市在“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司.某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图像是顶点为原点的抛物线的一部分(如图1所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图像是如图2所示的一条线段.生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式,并求年产量为多少万件时,所获毛利润最大?最大毛利润是多少?
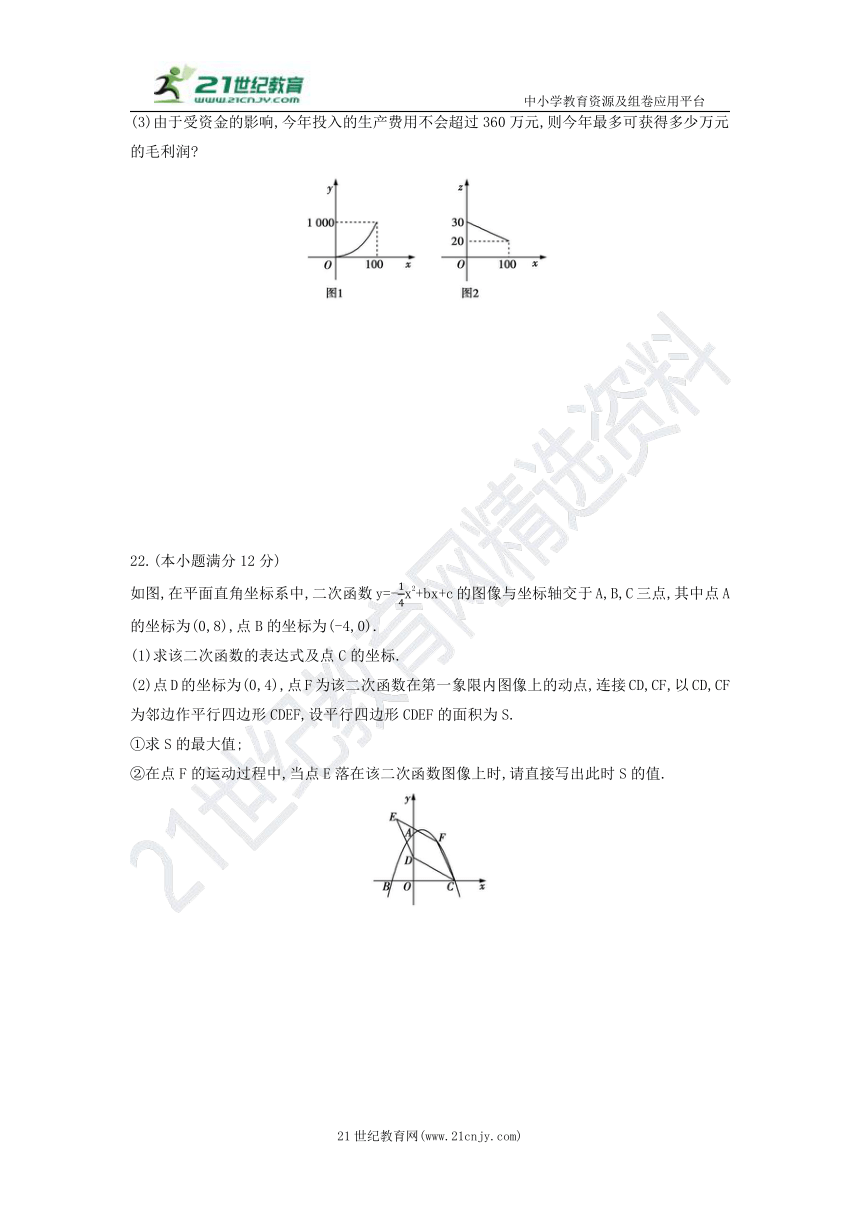
(3)由于受资金的影响,今年投入的生产费用不会超过360万元,则今年最多可获得多少万元的毛利润?
22.(本小题满分12分)
如图,在平面直角坐标系中,二次函数y=-14x2+bx+c的图像与坐标轴交于A,B,C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
(1)求该二次函数的表达式及点C的坐标.
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图像上的动点,连接CD,CF,以CD,CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请直接写出此时S的值.
参考答案与解析
1.C 【解析】 A选项,是一次函数,故不符合题意;B选项,y=(x-1)2-x2=1-2x,是一次函数,故不符合题意;C选项,y=2x2-7是二次函数,符合题意;D选项,y与x2是反比例关系,故不符合题意.故选C.
2.B 【解析】 ∵x=-3和x=-1对应的函数值都是-3,∴二次函数图像的对称轴为直线x=-2.故选B.
3.D 【解析】 根据题意,得y=(a-5)x2-3x+7,∵二次函数y=ax2-3x+7-5x2的图像有最低点,∴a-5>0,∴a>5.故选D.
4.B 【解析】 二次函数y=-14x2+x-4图像的对称轴为直线x=-12×(-14)=2,顶点坐标为(2,-3),显然选项C错误;∵a=-14<0,∴抛物线开口向下,顶点为最高点,当x=2时,y有最大值-3,故选项B正确;由抛物线开口向下,对称轴为直线x=2可知,当x>2时,y随x的增大而减小,故选项A错误;一元二次方程-14x2+x-4=0中,b2-4ac=1-4×(-14)×(-4)=-3<0,∴抛物线y=-14x2+x-4与x轴没有交点,故选项D错误.故选B.
5.A 【解析】 解法一 由题意可得抛物线y=(x-1)2-4向左平移2个单位长度,再向上平移3个单位长度,得到y=(x-1+2)2-4+3=x2+2x的图像,∴b=2,c=0.故选A.
解法二 抛物线y=(x-1)2-4的顶点坐标为(1,-4),将顶点向左平移2个单位长度,再向上平移3个单位长度,所得顶点坐标为(-1,-1),∴平移前的抛物线的表达式为y=(x+1)2-1,即y=x2+2x,∴b=2,c=0.故选A.
6.D 【解析】 A,B选项,由二次函数的图像可知a<0,对称轴在y轴的右侧,可知a,b异号,b>0,此时直线y=ax+b应经过第一、二、四象限,故A,B错误;C,D选项,由二次函数的图像可知a>0,对称轴在y轴的右侧,可知a,b异号,b<0,此时直线y=ax+b应经过第一、三、四象限,故C错误,D正确.故选D.
7.A 【解析】 ∵当x>2时,y随x的增大而增大,∴--(2m-1)2≤2,解得m≤2.5.∵抛物线开口向上,且不经过第三象限,∴2m≥0,解得m≥0,∴0≤m≤2.5.故选A.
8.C 【解析】 ∵y=-n2+14n-24=-(n-2)(n-12),∴当y=0时,n=2或n=12,又∵该函数的图像开口向下,∴1月,y<0;2月、12月,y=0.∴该企业一年中应停产的月份是1月、2月、12月.故选C.
9.B 【解析】 根据正方形的四条边相等,四个角都是直角,且AE=BF=CG=DH,可得△AEH≌△BFE≌△CGF≌△DHG.∵AE=x,则AH=1-x,根据勾股定理,得EH2=AE2+AH2=x2+(1-x)2,∴y=EH2=x2+(1-x)2=2x2-2x+1,010.A 【解析】 ∵一次函数y=-x与二次函数y=ax2+bx+c的图像有两个交点,∴方程ax2+bx+c=-x有两个不相等的实数根,即ax2+(b+1)x+c=0有两个不相等的实数根.故选A.
11.C 【解析】 由题意可设抛物线为y=a(x-6)2+2.6,∵抛物线y=a(x-6)2+2.6过点(0,2),∴2=a(0-6)2+2.6,解得a=-160,故y与x之间的关系式为y=-160(x-6)2+2.6.当x=9时,y=-160(9-6)2+2.6=2.45>2.43,∴球能过球网;当y=0时,-160(x-6)2+2.6=0,解得x1=6+239>18,x2=6-239(舍去),故球会出界.故选C.
12.C 【解析】 对于y=-(x-m)2+m2+1,易知抛物线的开口向下,对称轴为直线x=m,顶点坐标为(m,m2+1).当-2≤m≤1时,最大值为m2+1=4,解得m1=3(不合题意,舍去),m2=-3.当m<-2时,易知当x=-2时有最大值,即-(-2-m)2+m2+1=4,解得m=-74(不合题意,舍去).当m>1时,易知当x=1时有最大值,即-(1-m)2+m2+1=4,解得m=2.综上可知,m的值为2或-3.故选C.
13.> 【解析】 ∵二次函数y=ax2+bx+c的图像的对称轴为直线x=1且a>0,而1-(-1)=2,2-1=1,∴点(-1,y1)离对称轴的距离比点(2,y2)远,∴y1>y2.
14.1.6 【解析】 由题意得t=4时,h=0,则0=16a+1.6×4,解得a=-0.4,∴h=-0.4t2+1.6t,∴铅球距地面的最大高度是4ac-b24a=4×(-0.4)×0-1.624×(-0.4)=1.6(m).
15.甲 【解析】 将四人的结论转化如下,甲:b=2a,且a>0,b>0.乙:4a-2b+c=0.丙:a<0,且-b2a≥1.丁:25a+5b+c=-4.由于甲、丙发现的结论中,a正负恰好相反,则两人的结论中必有一个错误,因此乙、丁正确,所以21a+7b=-4.若甲正确,则将b=2a代入21a+7b=-4,得a=-435,b=-835,与甲的结论a>0,b>0矛盾,所以甲错误,丙正确.
16.2 【解析】 如图,过点C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H.∵A(0,2),B(1,0),∴OA=2,OB=1,∵四边形ABCD为正方形,∴∠ABC=90°,AB=BC,∴∠ABO+∠CBG=90°,∵∠ABO+∠OAB=90°,∴∠CBG=∠OAB,∵∠AOB=∠BGC=90°,∴△AOB≌△BGC,∴BG=OA=2,CG=OB=1,∴C(3,1).同理得△BCG≌△CDH,∴CH=BG=2,DH=CG=1,∴D(2,3).∵点C在抛物线y=13x2+bx-1上,把C(3,1)代入得b=-13,∴y=13x2-13x-1.设D'(x,y),由平移得D与D'的纵坐标相同,则y=3.当y=3时,13x2-13x-1=3,解得x1=4,x2=-3(舍去),∴DD'=4-2=2,则点D与其对应点D'间的距离为2.
17.【解析】 (1)x1=-1,x2=3
(2)设抛物线的表达式为y=-(x-1)2+m,
∵抛物线与x轴交于点(3,0),∴-(3-1)2+m=0,解得m=4,
∴抛物线的表达式为y=-(x-1)2+4,即y=-x2+2x+3.(3)k>4.
18.【解析】 (1)以桥孔的最高点为原点,建立如图所示的平面直角坐标系,设水面与抛物线的交点分别为A,B,水面上升1m后,与抛物线的交点分别为C,D.
由题意知A(3,-3),B(-3,-3),设抛物线的表达式为y=ax2,
把点B坐标代入,得9a=-3,解得a=-13,所以抛物线的表达式为y=-13x2,
当y=-2时,-13x2=-2,解得x=±6,故暴雨后水面的宽度为26m.
(2)由(1)知,当x=2时,y=-43,因为-43-(-2)=23>0.5,所以暴雨后这艘船能从桥下通过.
19.【解析】 (1)∵AB=2,抛物线的对称轴为直线x=2,
∴点A的坐标为(1,0),点B的坐标为(3,0).
∴抛物线的表达式为y=(x-1)(x-3)=x2-4x+3.
(2)如图,连接AC,BC,BC交对称轴于点P,连接PA.
由(1)知抛物线的表达式为y=x2-4x+3,
∴点C的坐标为(0,3),又∵点A,B的坐标分别为(1,0),(3,0),
∴BC=32+32=32,AC=32+12=10.∵点A,B关于直线x=2对称,
∴PA=PB,∴PA+PC=PB+PC,此时,PB+PC=BC,
∴当点P在对称轴上运动时,PA+PC的最小值为BC,∴△APC周长的最小值为AC+AP+PC=BC+AC=32+10.
20.【解析】 (1)①∵m=2,∴抛物线的表达式为y=x2-2x+n.
∵x=--22=1,∴抛物线的对称轴为直线x=1.
当x=1时,y=1-2+n=n-1,∴顶点的纵坐标为n-1.
②x2<-2或x2>4
∵抛物线的对称轴为直线x=1,开口向上,
直线x=-2到直线x=1的距离为3,
点A(-2,y1),B(x2,y2)都在抛物线上,且y2>y1,∴x2的取值范围是x2<-2或x2>4.
(2)∵点P(-1,2),向右平移4个单位长度,得到点Q,
∴点Q的坐标为(3,2).
∵n=3,∴抛物线为y=x2-mx+3.
当抛物线经过点Q(3,2)时,32-3m+3=2,解得m=103;
当抛物线经过点P(-1,2)时,(-1)2+m+3=2,解得m=-2;
当抛物线的顶点在线段PQ上时,12-m24=2,解得m=±2.
分别画出y=x2-103x+3,y=x2-2x+3,y=x2+2x+3的图像及线段PQ,如图所示,
结合图像可知,m的取值范围是m≤-2或m=2或m>103.
21.【解析】 (1)y与x之间的函数关系式是y=110x2(0≤x≤100),z与x之间的函数关系式是z=-110x+30(0≤x≤100).由题图1可得函数图像经过点(100,1000),
设抛物线的表达式为y=ax2(a≠0),将点(100,1000)代入,得1000=10000a,解得a=110,
故y与x之间的函数关系式为y=110x2(0≤x≤100).
由题图2可得,函数图像经过点(0,30),(100,20),设z=kx+b,则100k+b=20,b=30,
解得k=-110,b=30.故z与x之间的函数关系式为z=-110x+30(0≤x≤100).
(2)w=zx-y=-110x2+30x-110x2=-15x2+30x=-15(x2-150x)=-15(x-75)2+1125(0≤x≤100),
∵-15<0,∴当x=75时,w有最大值,最大值为1125,
∴年产量为75万件时,所获毛利润最大,最大毛利润为1125万元.
(3)令y=360,得110x2=360,解得x=±60(负值舍去),
当0当0答:今年最多可获得毛利润1080万元.
22.【解析】 (1)把A(0,8),B(-4,0)代入y=-14x2+bx+c得
-4-4b+c=0,c=8,解得b=1,c=8,
∴该二次函数的表达式为y=-14x2+x+8.
当y=0时,-14x2+x+8=0,解得x1=-4,x2=8,
∴点C的坐标为(8,0).
(2)①如图,连接OF,DF,设F(t,-14t2+t+8),
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF-S△OCD=12×4×t+12×8×(-14t2+t+8)-12×4×8=-t2+6t+16=-(t-3)2+25.
当t=3时,△CDF的面积最大,最大值为25,
∵四边形CDEF为平行四边形,
∴S的最大值为50.
②18.
∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF.
∵点C向左平移8个单位长度,再向上平移4个单位长度得到点D,
∴点F向左平移8个单位长度,再向上平移4个单位长度得到点E,即E(t-8,-14t2+t+12).
∵E(t-8,-14t2+t+12)在抛物线上,
∴-14(t-8)2+t-8+8=-14t2+t+12,解得t=7,
当t=7时,S△CDF=-(7-3)2+25=9,
此时S=2S△CDF=18.
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数属于二次函数的是 ( )
A.y=2x+1 B.y=(x-1)2-x2 C.y=2x2-7 D.y=-1x2
2.二次函数y=ax2+bx+c(a≠0)图像上部分点的坐标(x,y)对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图像的对称轴是 ( )
A.直线x=-3 B.直线x=-2 C.直线x=-1 D.直线x=0
3.若二次函数y=ax2-3x+7-5x2的图像有最低点,则a的值可以是 ( )
A.0 B.2 C.4 D.6
4.对于二次函数y=-14x2+x-4,下列说法正确的是 ( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图像的顶点坐标为(-2,-7) D.图像与x轴有两个交点
5.将二次函数y=x2+bx+c的图像先向右平移2个单位长度,再向下平移3个单位长度,所得图像的函数表达式为y=(x-1)2-4,则b,c的值分别为 ( )
A.2,0 B.2,-6 C.-6,8 D.-6,2
6.下列是抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图像的是 ( )
7.已知抛物线y=x2-(2m-1)x+2m不经过第三象限,且当x>2时,y随x的增大而增大,则实数m的取值范围是 ( )
A.0≤m≤2.5 B.m≥1.5 C.0≤m≤1.5 D.0
A.1月、2月、3月 B.2月、3月、4月 C.1月、2月、12月 D.1月、11月、12月
9.如图,正方形ABCD的边长为1,E,F,G,H分别为各边上的点,且AE=BF=CG=DH,设AE为x,小正方形EFGH的面积为y,则y关于x的函数对应的图像大致是 ( )
10.如图,一次函数y=-x与二次函数y=ax2+bx+c的图像相交于点M,N,则关于x的一元二次方程ax2+(b+1)x+c=0的根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上结论都正确
第10题图 第11题图
11.如图,排球运动员站在O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-h)2+k.已知球与O点的水平距离为6m时,球运行的高度达到最高2.6m,球网BC的高度为2.43m,与O点的水平距离为9m.球场的边界距O点的水平距离为18m,则下列判断正确的是 ( )
A.球不会过球网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
12.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为 ( )
A.-74 B.3或-3 C.2或-3 D.2或-3或-74
二、填空题(本大题共4小题,每小题3分,共12分)
13.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)?
14.如图,铅球被小明从手中抛出,铅球距地面的高度h(m)与抛出时间t(s)之间满足函数关系h=at2+1.6t,已知铅球被抛出后经过4s落地,则铅球距地面的最大高度是 m.?
15.四位同学在研究二次函数y=ax2+bx+c(a,b,c是常数,a≠0)时,甲发现当x=-1时,函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是 .?
25317459550400016.如图,在平面直角坐标系中,正方形ABCD的顶点A,B的坐标分别为(0,2),(1,0),顶点C在函数y=13x2+bx-1的图像上,将正方形ABCD沿x轴平移后得到正方形A'B'C'D',点D的对应点D'落在抛物线y=13x2+bx-1上,则点D与其对应点D'间的距离为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分6分)
已知二次函数y=-x2+bx+c的图像如图所示.
(1)关于x的一元二次方程-x2+bx+c=0的解为 ;?
(2)求此抛物线的表达式;
(3)若直线y=k与抛物线没有交点,直接写出k的范围.
18.(本小题满分8分)
河上有一座桥孔为抛物线形的拱桥(如图1),水面宽6m时,水面距离桥孔顶部3m,因降暴雨水面上升1m.
(1)建立适当的坐标系,并求暴雨后水面的宽度;
(2)一艘装满物资的小船,露出水面的部分高0.5m、宽4m(横断面如图2所示),暴雨后这艘船能从这座拱桥下通过吗?(注:结果保留根号)
19.(本小题满分8分)
如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值.
20.(本小题满分8分)
在平面直角坐标系xOy中,已知抛物线y=x2-mx+n.
(1)当m=2时,
①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(-2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是 .?
(2)已知点P(-1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,抛物线与线段PQ恰有一个交点,结合函数图像,求m的取值范围.
21.(本小题满分10分)
某市在“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司.某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图像是顶点为原点的抛物线的一部分(如图1所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图像是如图2所示的一条线段.生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式,并求年产量为多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入的生产费用不会超过360万元,则今年最多可获得多少万元的毛利润?
22.(本小题满分12分)
如图,在平面直角坐标系中,二次函数y=-14x2+bx+c的图像与坐标轴交于A,B,C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
(1)求该二次函数的表达式及点C的坐标.
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图像上的动点,连接CD,CF,以CD,CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请直接写出此时S的值.
参考答案与解析
1.C 【解析】 A选项,是一次函数,故不符合题意;B选项,y=(x-1)2-x2=1-2x,是一次函数,故不符合题意;C选项,y=2x2-7是二次函数,符合题意;D选项,y与x2是反比例关系,故不符合题意.故选C.
2.B 【解析】 ∵x=-3和x=-1对应的函数值都是-3,∴二次函数图像的对称轴为直线x=-2.故选B.
3.D 【解析】 根据题意,得y=(a-5)x2-3x+7,∵二次函数y=ax2-3x+7-5x2的图像有最低点,∴a-5>0,∴a>5.故选D.
4.B 【解析】 二次函数y=-14x2+x-4图像的对称轴为直线x=-12×(-14)=2,顶点坐标为(2,-3),显然选项C错误;∵a=-14<0,∴抛物线开口向下,顶点为最高点,当x=2时,y有最大值-3,故选项B正确;由抛物线开口向下,对称轴为直线x=2可知,当x>2时,y随x的增大而减小,故选项A错误;一元二次方程-14x2+x-4=0中,b2-4ac=1-4×(-14)×(-4)=-3<0,∴抛物线y=-14x2+x-4与x轴没有交点,故选项D错误.故选B.
5.A 【解析】 解法一 由题意可得抛物线y=(x-1)2-4向左平移2个单位长度,再向上平移3个单位长度,得到y=(x-1+2)2-4+3=x2+2x的图像,∴b=2,c=0.故选A.
解法二 抛物线y=(x-1)2-4的顶点坐标为(1,-4),将顶点向左平移2个单位长度,再向上平移3个单位长度,所得顶点坐标为(-1,-1),∴平移前的抛物线的表达式为y=(x+1)2-1,即y=x2+2x,∴b=2,c=0.故选A.
6.D 【解析】 A,B选项,由二次函数的图像可知a<0,对称轴在y轴的右侧,可知a,b异号,b>0,此时直线y=ax+b应经过第一、二、四象限,故A,B错误;C,D选项,由二次函数的图像可知a>0,对称轴在y轴的右侧,可知a,b异号,b<0,此时直线y=ax+b应经过第一、三、四象限,故C错误,D正确.故选D.
7.A 【解析】 ∵当x>2时,y随x的增大而增大,∴--(2m-1)2≤2,解得m≤2.5.∵抛物线开口向上,且不经过第三象限,∴2m≥0,解得m≥0,∴0≤m≤2.5.故选A.
8.C 【解析】 ∵y=-n2+14n-24=-(n-2)(n-12),∴当y=0时,n=2或n=12,又∵该函数的图像开口向下,∴1月,y<0;2月、12月,y=0.∴该企业一年中应停产的月份是1月、2月、12月.故选C.
9.B 【解析】 根据正方形的四条边相等,四个角都是直角,且AE=BF=CG=DH,可得△AEH≌△BFE≌△CGF≌△DHG.∵AE=x,则AH=1-x,根据勾股定理,得EH2=AE2+AH2=x2+(1-x)2,∴y=EH2=x2+(1-x)2=2x2-2x+1,0
11.C 【解析】 由题意可设抛物线为y=a(x-6)2+2.6,∵抛物线y=a(x-6)2+2.6过点(0,2),∴2=a(0-6)2+2.6,解得a=-160,故y与x之间的关系式为y=-160(x-6)2+2.6.当x=9时,y=-160(9-6)2+2.6=2.45>2.43,∴球能过球网;当y=0时,-160(x-6)2+2.6=0,解得x1=6+239>18,x2=6-239(舍去),故球会出界.故选C.
12.C 【解析】 对于y=-(x-m)2+m2+1,易知抛物线的开口向下,对称轴为直线x=m,顶点坐标为(m,m2+1).当-2≤m≤1时,最大值为m2+1=4,解得m1=3(不合题意,舍去),m2=-3.当m<-2时,易知当x=-2时有最大值,即-(-2-m)2+m2+1=4,解得m=-74(不合题意,舍去).当m>1时,易知当x=1时有最大值,即-(1-m)2+m2+1=4,解得m=2.综上可知,m的值为2或-3.故选C.
13.> 【解析】 ∵二次函数y=ax2+bx+c的图像的对称轴为直线x=1且a>0,而1-(-1)=2,2-1=1,∴点(-1,y1)离对称轴的距离比点(2,y2)远,∴y1>y2.
14.1.6 【解析】 由题意得t=4时,h=0,则0=16a+1.6×4,解得a=-0.4,∴h=-0.4t2+1.6t,∴铅球距地面的最大高度是4ac-b24a=4×(-0.4)×0-1.624×(-0.4)=1.6(m).
15.甲 【解析】 将四人的结论转化如下,甲:b=2a,且a>0,b>0.乙:4a-2b+c=0.丙:a<0,且-b2a≥1.丁:25a+5b+c=-4.由于甲、丙发现的结论中,a正负恰好相反,则两人的结论中必有一个错误,因此乙、丁正确,所以21a+7b=-4.若甲正确,则将b=2a代入21a+7b=-4,得a=-435,b=-835,与甲的结论a>0,b>0矛盾,所以甲错误,丙正确.
16.2 【解析】 如图,过点C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H.∵A(0,2),B(1,0),∴OA=2,OB=1,∵四边形ABCD为正方形,∴∠ABC=90°,AB=BC,∴∠ABO+∠CBG=90°,∵∠ABO+∠OAB=90°,∴∠CBG=∠OAB,∵∠AOB=∠BGC=90°,∴△AOB≌△BGC,∴BG=OA=2,CG=OB=1,∴C(3,1).同理得△BCG≌△CDH,∴CH=BG=2,DH=CG=1,∴D(2,3).∵点C在抛物线y=13x2+bx-1上,把C(3,1)代入得b=-13,∴y=13x2-13x-1.设D'(x,y),由平移得D与D'的纵坐标相同,则y=3.当y=3时,13x2-13x-1=3,解得x1=4,x2=-3(舍去),∴DD'=4-2=2,则点D与其对应点D'间的距离为2.
17.【解析】 (1)x1=-1,x2=3
(2)设抛物线的表达式为y=-(x-1)2+m,
∵抛物线与x轴交于点(3,0),∴-(3-1)2+m=0,解得m=4,
∴抛物线的表达式为y=-(x-1)2+4,即y=-x2+2x+3.(3)k>4.
18.【解析】 (1)以桥孔的最高点为原点,建立如图所示的平面直角坐标系,设水面与抛物线的交点分别为A,B,水面上升1m后,与抛物线的交点分别为C,D.
由题意知A(3,-3),B(-3,-3),设抛物线的表达式为y=ax2,
把点B坐标代入,得9a=-3,解得a=-13,所以抛物线的表达式为y=-13x2,
当y=-2时,-13x2=-2,解得x=±6,故暴雨后水面的宽度为26m.
(2)由(1)知,当x=2时,y=-43,因为-43-(-2)=23>0.5,所以暴雨后这艘船能从桥下通过.
19.【解析】 (1)∵AB=2,抛物线的对称轴为直线x=2,
∴点A的坐标为(1,0),点B的坐标为(3,0).
∴抛物线的表达式为y=(x-1)(x-3)=x2-4x+3.
(2)如图,连接AC,BC,BC交对称轴于点P,连接PA.
由(1)知抛物线的表达式为y=x2-4x+3,
∴点C的坐标为(0,3),又∵点A,B的坐标分别为(1,0),(3,0),
∴BC=32+32=32,AC=32+12=10.∵点A,B关于直线x=2对称,
∴PA=PB,∴PA+PC=PB+PC,此时,PB+PC=BC,
∴当点P在对称轴上运动时,PA+PC的最小值为BC,∴△APC周长的最小值为AC+AP+PC=BC+AC=32+10.
20.【解析】 (1)①∵m=2,∴抛物线的表达式为y=x2-2x+n.
∵x=--22=1,∴抛物线的对称轴为直线x=1.
当x=1时,y=1-2+n=n-1,∴顶点的纵坐标为n-1.
②x2<-2或x2>4
∵抛物线的对称轴为直线x=1,开口向上,
直线x=-2到直线x=1的距离为3,
点A(-2,y1),B(x2,y2)都在抛物线上,且y2>y1,∴x2的取值范围是x2<-2或x2>4.
(2)∵点P(-1,2),向右平移4个单位长度,得到点Q,
∴点Q的坐标为(3,2).
∵n=3,∴抛物线为y=x2-mx+3.
当抛物线经过点Q(3,2)时,32-3m+3=2,解得m=103;
当抛物线经过点P(-1,2)时,(-1)2+m+3=2,解得m=-2;
当抛物线的顶点在线段PQ上时,12-m24=2,解得m=±2.
分别画出y=x2-103x+3,y=x2-2x+3,y=x2+2x+3的图像及线段PQ,如图所示,
结合图像可知,m的取值范围是m≤-2或m=2或m>103.
21.【解析】 (1)y与x之间的函数关系式是y=110x2(0≤x≤100),z与x之间的函数关系式是z=-110x+30(0≤x≤100).由题图1可得函数图像经过点(100,1000),
设抛物线的表达式为y=ax2(a≠0),将点(100,1000)代入,得1000=10000a,解得a=110,
故y与x之间的函数关系式为y=110x2(0≤x≤100).
由题图2可得,函数图像经过点(0,30),(100,20),设z=kx+b,则100k+b=20,b=30,
解得k=-110,b=30.故z与x之间的函数关系式为z=-110x+30(0≤x≤100).
(2)w=zx-y=-110x2+30x-110x2=-15x2+30x=-15(x2-150x)=-15(x-75)2+1125(0≤x≤100),
∵-15<0,∴当x=75时,w有最大值,最大值为1125,
∴年产量为75万件时,所获毛利润最大,最大毛利润为1125万元.
(3)令y=360,得110x2=360,解得x=±60(负值舍去),
当0
22.【解析】 (1)把A(0,8),B(-4,0)代入y=-14x2+bx+c得
-4-4b+c=0,c=8,解得b=1,c=8,
∴该二次函数的表达式为y=-14x2+x+8.
当y=0时,-14x2+x+8=0,解得x1=-4,x2=8,
∴点C的坐标为(8,0).
(2)①如图,连接OF,DF,设F(t,-14t2+t+8),
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF-S△OCD=12×4×t+12×8×(-14t2+t+8)-12×4×8=-t2+6t+16=-(t-3)2+25.
当t=3时,△CDF的面积最大,最大值为25,
∵四边形CDEF为平行四边形,
∴S的最大值为50.
②18.
∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF.
∵点C向左平移8个单位长度,再向上平移4个单位长度得到点D,
∴点F向左平移8个单位长度,再向上平移4个单位长度得到点E,即E(t-8,-14t2+t+12).
∵E(t-8,-14t2+t+12)在抛物线上,
∴-14(t-8)2+t-8+8=-14t2+t+12,解得t=7,
当t=7时,S△CDF=-(7-3)2+25=9,
此时S=2S△CDF=18.
