第32章 投影与视图 单元测试卷(含解析)
文档属性
| 名称 | 第32章 投影与视图 单元测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览

文档简介
冀教版九年级数学下册第32章投影与视图
单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
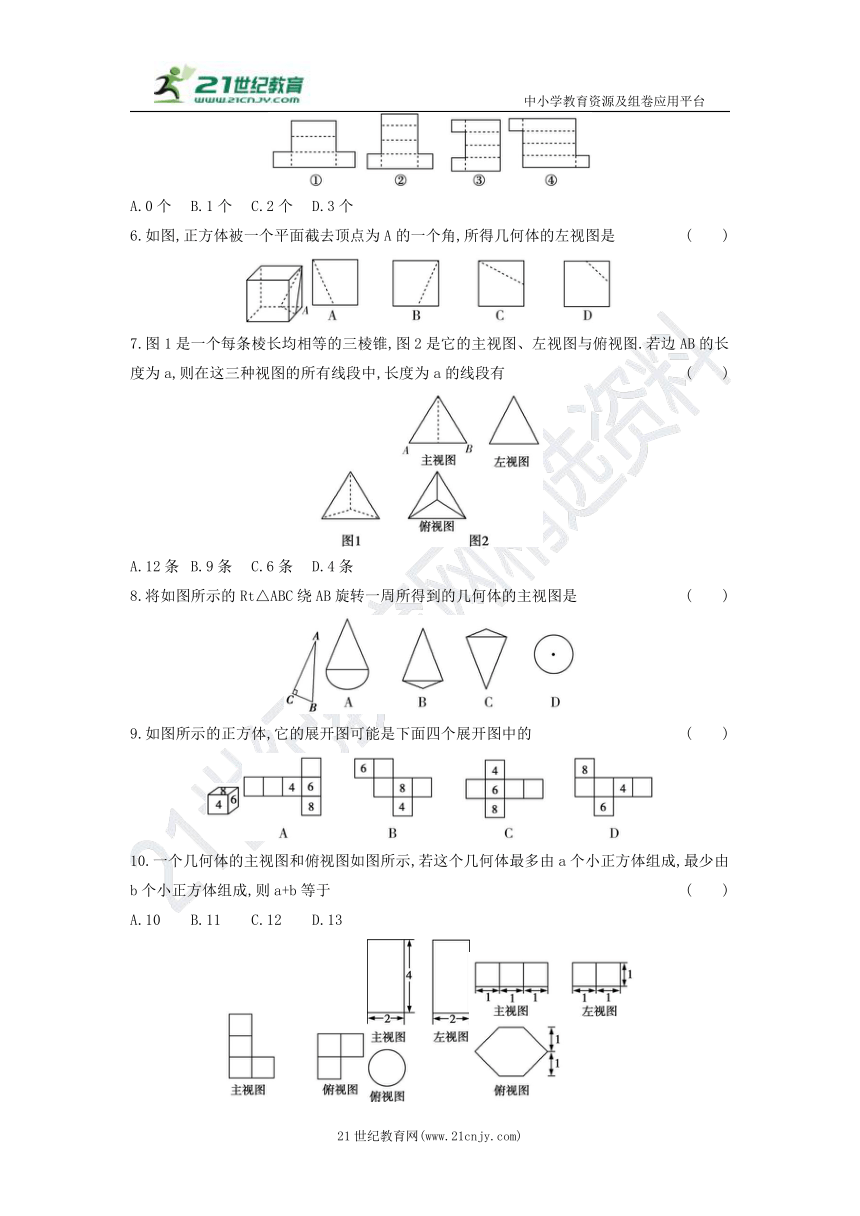
1.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的是 ( )
2.如图是由四个相同的小正方体组成的立体图形,它的俯视图为 ( )
A B C D
3.如图,晚上小明在路灯下散步,在小明由A处走到B处的这一过程中,他在地上的影子 ( )
A.逐渐变短 B.逐渐变长 C.先变短后变长 D.先变长后变短
-48260891540004.毕业前夕,同学们准备了一份礼物送给自己的母校.现用一个正方体盒子进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上.则此包装盒的展开图(不考虑文字方向)不可能是 ( )
5.下列四个图形能围成棱柱的有 ( )
A.0个 B.1个 C.2个 D.3个
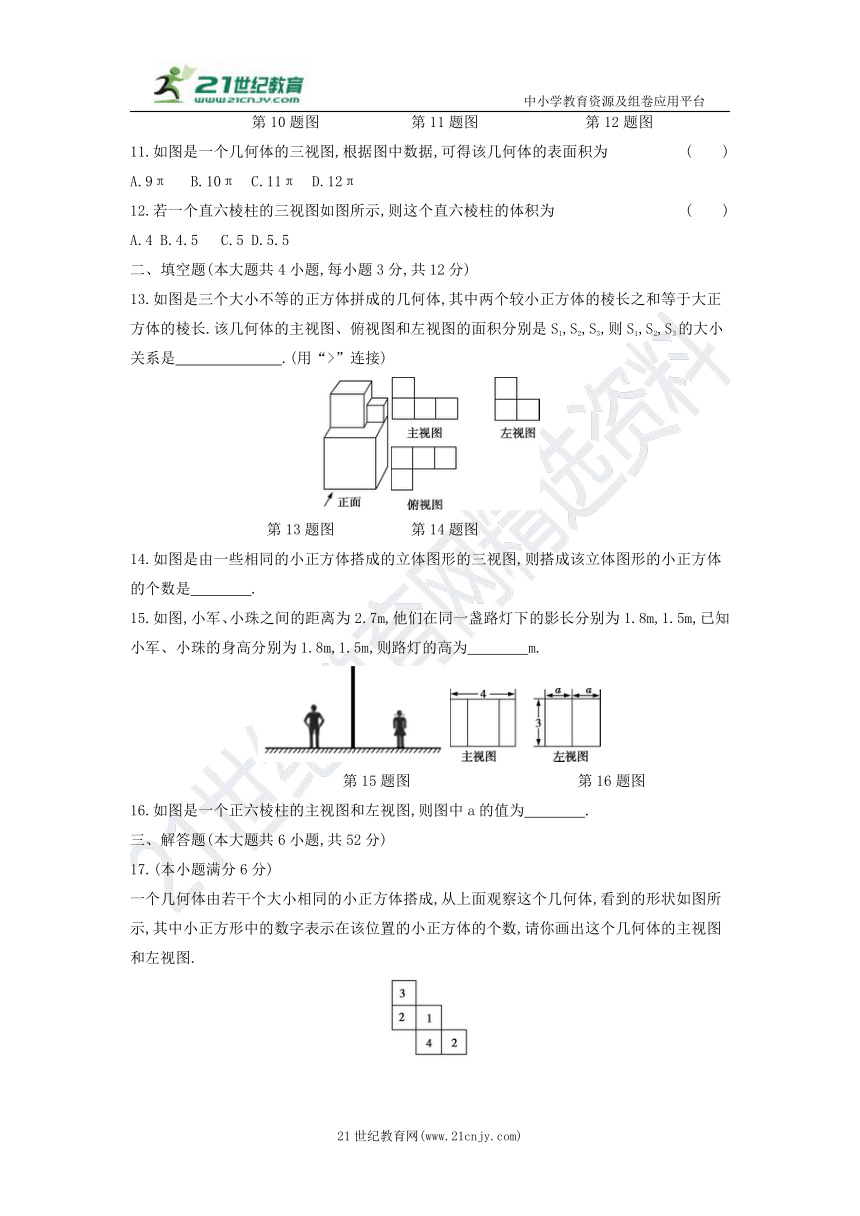
6.如图,正方体被一个平面截去顶点为A的一个角,所得几何体的左视图是 ( )
7.图1是一个每条棱长均相等的三棱锥,图2是它的主视图、左视图与俯视图.若边AB的长度为a,则在这三种视图的所有线段中,长度为a的线段有 ( )
A.12条 B.9条 C.6条 D.4条
8.将如图所示的Rt△ABC绕AB旋转一周所得到的几何体的主视图是 ( )
9.如图所示的正方体,它的展开图可能是下面四个展开图中的 ( )
10.一个几何体的主视图和俯视图如图所示,若这个几何体最多由a个小正方体组成,最少由b个小正方体组成,则a+b等于 ( )
A.10 B.11 C.12 D.13
第10题图 第11题图 第12题图
11.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为 ( )
A.9π B.10π C.11π D.12π
12.若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为 ( )
A.4 B.4.5 C.5 D.5.5
二、填空题(本大题共4小题,每小题3分,共12分)
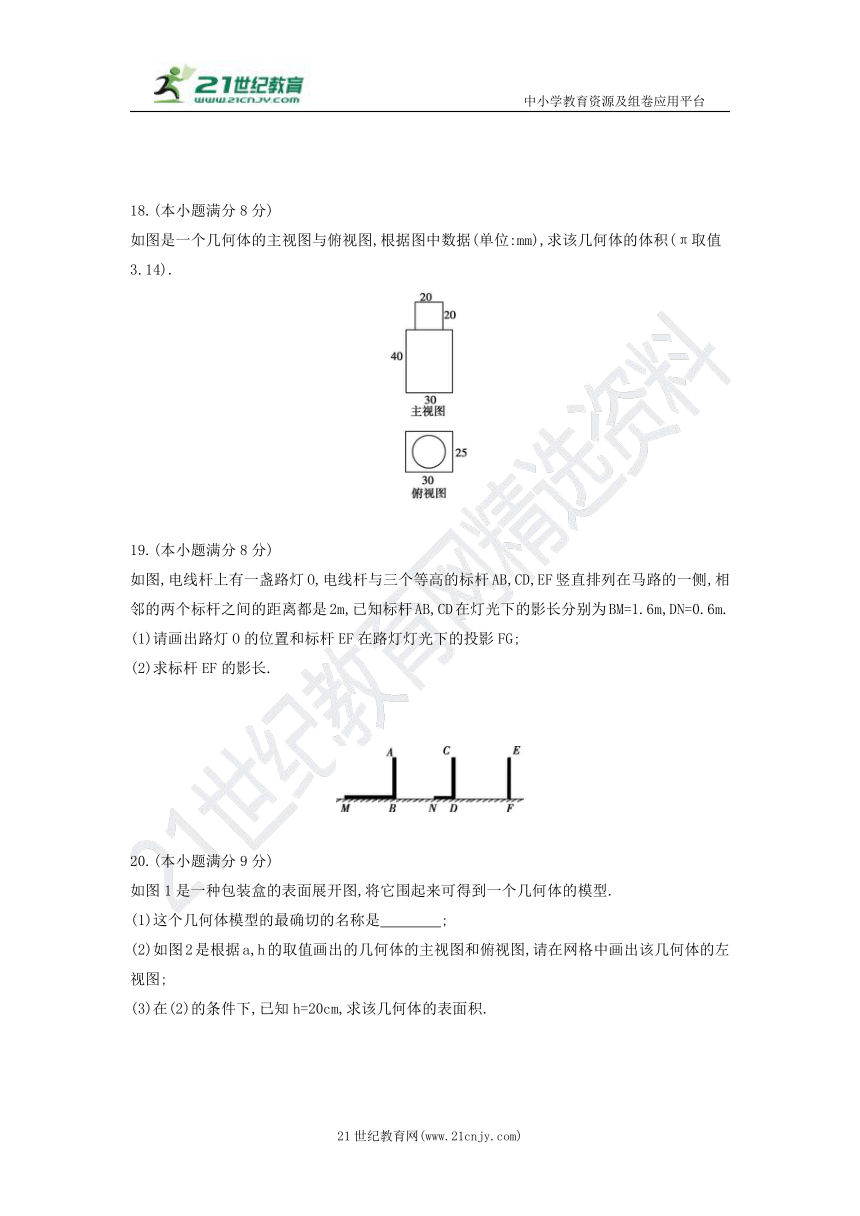
13.如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是 .(用“>”连接)?
第13题图 第14题图
14.如图是由一些相同的小正方体搭成的立体图形的三视图,则搭成该立体图形的小正方体的个数是 .?
15.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为 m.?
第15题图 第16题图
16.如图是一个正六棱柱的主视图和左视图,则图中a的值为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分6分)
一个几何体由若干个大小相同的小正方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数,请你画出这个几何体的主视图和左视图.
18.(本小题满分8分)
如图是一个几何体的主视图与俯视图,根据图中数据(单位:mm),求该几何体的体积(π取值3.14).
19.(本小题满分8分)
如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆AB,CD,EF竖直排列在马路的一侧,相邻的两个标杆之间的距离都是2m,已知标杆AB,CD在灯光下的影长分别为BM=1.6m,DN=0.6m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的投影FG;
(2)求标杆EF的影长.
20.(本小题满分9分)
如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的最确切的名称是 ;?
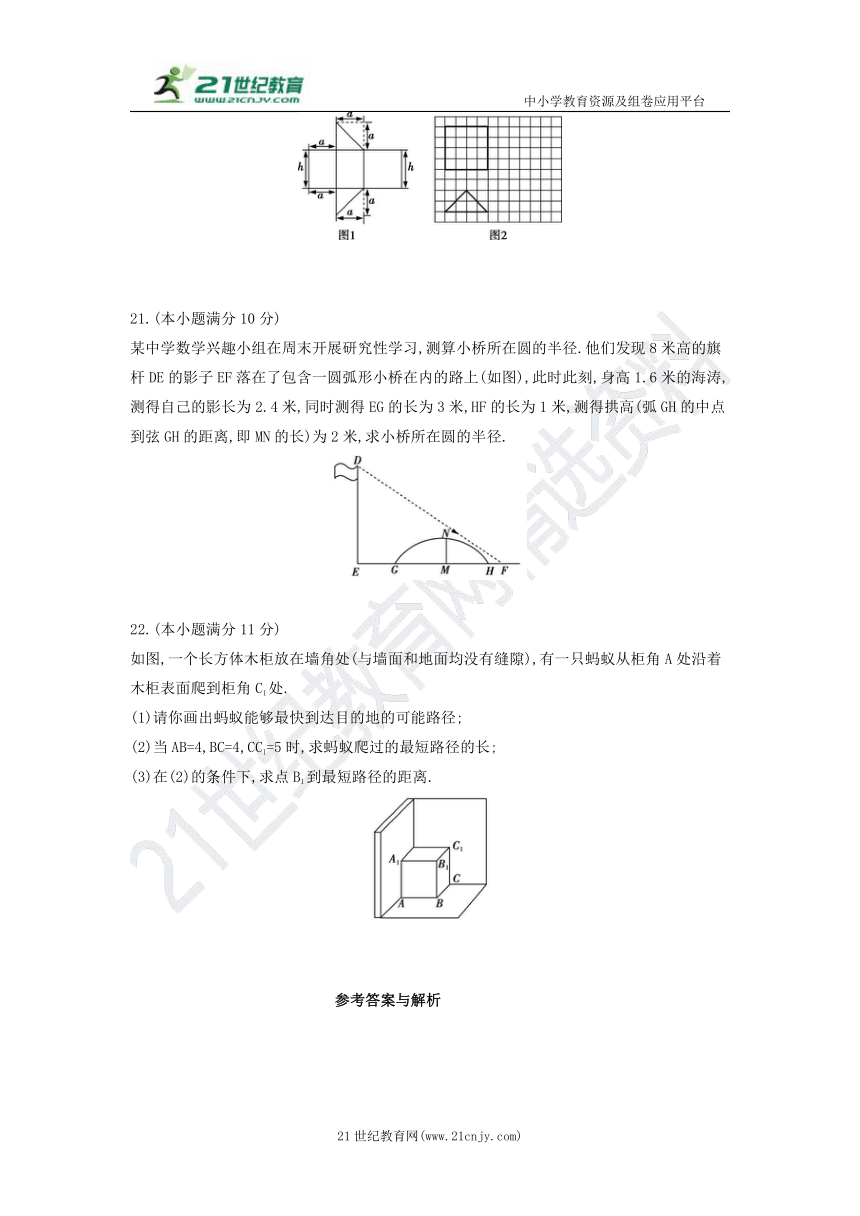
(2)如图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20cm,求该几何体的表面积.
21.(本小题满分10分)
某中学数学兴趣小组在周末开展研究性学习,测算小桥所在圆的半径.他们发现8米高的旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上(如图),此时此刻,身高1.6米的海涛,测得自己的影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
22.(本小题满分11分)
如图,一个长方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;
(3)在(2)的条件下,求点B1到最短路径的距离.
参考答案与解析
1.D 【解析】 A,B选项,两棵小树的影子的方向相反,不可能为同一时刻阳光下的影子,所以A,B选项错误;在同一时刻阳光下,树高与影子成正比,所以C选项错误,D选项正确.故选D.
2.B 【解析】 俯视图是从上面往下观察所得的图形,观察可知该立体图形的俯视图有2行,上面一行有2个小正方形,下面一行有1个小正方形,且位于左侧.故选B.
3.C 【解析】 路灯下的投影为中心投影,离路灯越近,影子越短,离路灯越远,影子越长.故选C.
4.D 【解析】 D项中的图形不能围成正方体,不符合题意.故选D.
5.C 【解析】 第①个图形缺少一个面,不能围成棱柱;第③个图形折叠后有两面重合,不能折成棱柱;第②个图形、第④个图形都能围成四棱柱.故选C.
6.A 【解析】 左视图是一个正方形,左下角部分是一个直角三角形,斜边是虚线.故选A.
7.D 【解析】 因为主视图中线段AB=a,所以该三棱锥的棱长为a,在主视图的三角形中只有底边长为a,左视图中没有长度为a的线段,俯视图中大三角形的三条边均为a,即三视图中长度为a的线段有4条,故选D.
8.B 【解析】 Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等且相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是由两个底边相等的等腰三角形组成,并且上面的等腰三角形较大,故选B.
9.A 【解析】 由原正方体的特征可知,含有4,6,8数字的三个面一定相交于一点,而选项B,C,D经过折叠后与含有4,6,8数字的三个面相交于一点不符.故选A.
10.C 【解析】 结合主视图和俯视图可知,左边后排最多有3个,左边前排最多有3个,右边只有1层,且只有1个,所以该几何体最多由7个小正方体组成.结合主视图和俯视图可知,左边前排、后排都是最少有1个,最多有3个,且左边前排和左边后排中至少有一个有3个小正方体.右边只有1层,且只有1个,所以该几何体最少由5个小正方体组成,所以a+b=12.故选C.
11.B 【解析】 观察三视图发现,该几何体为圆柱,因为圆柱的底面半径为1,高为4,所以其表面积为S侧+2S底=2π×4+2π×12=10π,故选B.
12.A 【解析】 由三视图可知,该直六棱柱的高为1,由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1,3,高为1,所以该几何体的体积为12×(1+3)×1×2×1=4.故选A.
13.S1>S3>S2 【解析】 主视图的面积是三个正方形的面积和,左视图的面积是两个较大正方形的面积和,俯视图的面积是一个正方形的面积,故S1>S3>S2.
14.5 【解析】 由俯视图可得此立体图形有2行、3列,最底层有4个小正方体.由左视图和主视图可得此立体图形共2层,且第2层只有1个小正方体,故构成该立体图形的小正方体的个数是5.
15.3 【解析】 如图,∵CD∥AB∥MN,∴△ABE∽△CDE,△ABF∽△MNF,∴CDAB=DEBE,FNFB=MNAB,即1.8AB=1.81.8+BD,1.51.5+2.7-BD=1.5AB,所以AB=3m.
16.3 【解析】 根据题中该正六棱柱的主视图和左视图画出其俯视图,如图所示,连接BC,过点A作AD⊥BC于点D.在△ABC中,AB=AC,∠BAC=120°,所以∠ACD=30°,可得AD=12AC,从而易得2AD+AC=4,所以AC=2,AD=1.在Rt△ACD中,由勾股定理,得CD=3,所以a的值为3.
17.【解析】 主视图和左视图如图所示.
18.【解析】 由主视图和俯视图可知,该几何体是由一个底面直径为20、高为20的圆柱和长、宽、高分别为30,25,40的长方体组成的,所以该几何体的体积为3.14×(20÷2)2×20+25×30×40=36280(mm3).
19.【解析】 (1)路灯O的位置及投影FG如图所示.
(2)如图,过O作OH⊥MG于点H,设DH=xm,
由AB∥CD∥OH,得MBMH=ABOH,NDNH=CDOH,
因为AB=CD,
所以MBMH=NDNH,即1.61.6+2+x=0.60.6+x,
所以x=1.2.
设FG=ym,同理得FGHG=NDNH,
即y2-1.2+y=0.60.6+1.2,
所以y=0.4.
所以EF的影长为0.4m.
20.【解析】 (1)直三棱柱
(2)如图所示.
(3)由题意可得a=h2=202=102(cm),
S表面积=12×(102)2×2+2×102×20+202=(600+4002)(cm2).
21.【解析】 ∵海涛身高1.6米,测得其影长为2.4米,
∴8米高的旗杆DE的影长为12米.
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(米),
∴GM=MH=4米.
如图,设小桥的圆心为O,连接OM,OG,易知OM⊥GH.
设小桥所在圆的半径为r,
∵MN=2米,∴OM=(r-2)米.
在Rt△OGM中,由勾股定理得OG2=OM2+GM2,
∴r2=(r-2)2+42,解得r=5.
答:小桥所在圆的半径为5米.
22.【解析】 (1)木柜露在外面的表面展开图如图所示,
则蚂蚁能够最快到达目的地的可能路径为AC'1或AC1.
(2)路径AC'1的长是42+(4+5)2=97.
路径AC1的长是(4+4)2+52=89.
因为97>89,所以蚂蚁爬过的最短路径的长是89.
(3)如图,过点B1作B1E⊥AC1于点E,易知B1E即点B1到最短路径的距离.
∵∠C1EB1=∠C1A1A=90°,∠EC1B1=∠A1C1A,
∴△B1EC1∽△AA1C1,
∴B1EAA1=B1C1AC1,∴B1E=B1C1AC1×AA1=489×5=208989.
单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的是 ( )
2.如图是由四个相同的小正方体组成的立体图形,它的俯视图为 ( )
A B C D
3.如图,晚上小明在路灯下散步,在小明由A处走到B处的这一过程中,他在地上的影子 ( )
A.逐渐变短 B.逐渐变长 C.先变短后变长 D.先变长后变短
-48260891540004.毕业前夕,同学们准备了一份礼物送给自己的母校.现用一个正方体盒子进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上.则此包装盒的展开图(不考虑文字方向)不可能是 ( )
5.下列四个图形能围成棱柱的有 ( )
A.0个 B.1个 C.2个 D.3个
6.如图,正方体被一个平面截去顶点为A的一个角,所得几何体的左视图是 ( )
7.图1是一个每条棱长均相等的三棱锥,图2是它的主视图、左视图与俯视图.若边AB的长度为a,则在这三种视图的所有线段中,长度为a的线段有 ( )
A.12条 B.9条 C.6条 D.4条
8.将如图所示的Rt△ABC绕AB旋转一周所得到的几何体的主视图是 ( )
9.如图所示的正方体,它的展开图可能是下面四个展开图中的 ( )
10.一个几何体的主视图和俯视图如图所示,若这个几何体最多由a个小正方体组成,最少由b个小正方体组成,则a+b等于 ( )
A.10 B.11 C.12 D.13
第10题图 第11题图 第12题图
11.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为 ( )
A.9π B.10π C.11π D.12π
12.若一个直六棱柱的三视图如图所示,则这个直六棱柱的体积为 ( )
A.4 B.4.5 C.5 D.5.5
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是 .(用“>”连接)?
第13题图 第14题图
14.如图是由一些相同的小正方体搭成的立体图形的三视图,则搭成该立体图形的小正方体的个数是 .?
15.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为 m.?
第15题图 第16题图
16.如图是一个正六棱柱的主视图和左视图,则图中a的值为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分6分)
一个几何体由若干个大小相同的小正方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数,请你画出这个几何体的主视图和左视图.
18.(本小题满分8分)
如图是一个几何体的主视图与俯视图,根据图中数据(单位:mm),求该几何体的体积(π取值3.14).
19.(本小题满分8分)
如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆AB,CD,EF竖直排列在马路的一侧,相邻的两个标杆之间的距离都是2m,已知标杆AB,CD在灯光下的影长分别为BM=1.6m,DN=0.6m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的投影FG;
(2)求标杆EF的影长.
20.(本小题满分9分)
如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的最确切的名称是 ;?
(2)如图2是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20cm,求该几何体的表面积.
21.(本小题满分10分)
某中学数学兴趣小组在周末开展研究性学习,测算小桥所在圆的半径.他们发现8米高的旗杆DE的影子EF落在了包含一圆弧形小桥在内的路上(如图),此时此刻,身高1.6米的海涛,测得自己的影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
22.(本小题满分11分)
如图,一个长方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;
(3)在(2)的条件下,求点B1到最短路径的距离.
参考答案与解析
1.D 【解析】 A,B选项,两棵小树的影子的方向相反,不可能为同一时刻阳光下的影子,所以A,B选项错误;在同一时刻阳光下,树高与影子成正比,所以C选项错误,D选项正确.故选D.
2.B 【解析】 俯视图是从上面往下观察所得的图形,观察可知该立体图形的俯视图有2行,上面一行有2个小正方形,下面一行有1个小正方形,且位于左侧.故选B.
3.C 【解析】 路灯下的投影为中心投影,离路灯越近,影子越短,离路灯越远,影子越长.故选C.
4.D 【解析】 D项中的图形不能围成正方体,不符合题意.故选D.
5.C 【解析】 第①个图形缺少一个面,不能围成棱柱;第③个图形折叠后有两面重合,不能折成棱柱;第②个图形、第④个图形都能围成四棱柱.故选C.
6.A 【解析】 左视图是一个正方形,左下角部分是一个直角三角形,斜边是虚线.故选A.
7.D 【解析】 因为主视图中线段AB=a,所以该三棱锥的棱长为a,在主视图的三角形中只有底边长为a,左视图中没有长度为a的线段,俯视图中大三角形的三条边均为a,即三视图中长度为a的线段有4条,故选D.
8.B 【解析】 Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等且相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是由两个底边相等的等腰三角形组成,并且上面的等腰三角形较大,故选B.
9.A 【解析】 由原正方体的特征可知,含有4,6,8数字的三个面一定相交于一点,而选项B,C,D经过折叠后与含有4,6,8数字的三个面相交于一点不符.故选A.
10.C 【解析】 结合主视图和俯视图可知,左边后排最多有3个,左边前排最多有3个,右边只有1层,且只有1个,所以该几何体最多由7个小正方体组成.结合主视图和俯视图可知,左边前排、后排都是最少有1个,最多有3个,且左边前排和左边后排中至少有一个有3个小正方体.右边只有1层,且只有1个,所以该几何体最少由5个小正方体组成,所以a+b=12.故选C.
11.B 【解析】 观察三视图发现,该几何体为圆柱,因为圆柱的底面半径为1,高为4,所以其表面积为S侧+2S底=2π×4+2π×12=10π,故选B.
12.A 【解析】 由三视图可知,该直六棱柱的高为1,由俯视图得六棱柱的底面可分成两个相同的等腰梯形,且梯形的上、下底边长分别为1,3,高为1,所以该几何体的体积为12×(1+3)×1×2×1=4.故选A.
13.S1>S3>S2 【解析】 主视图的面积是三个正方形的面积和,左视图的面积是两个较大正方形的面积和,俯视图的面积是一个正方形的面积,故S1>S3>S2.
14.5 【解析】 由俯视图可得此立体图形有2行、3列,最底层有4个小正方体.由左视图和主视图可得此立体图形共2层,且第2层只有1个小正方体,故构成该立体图形的小正方体的个数是5.
15.3 【解析】 如图,∵CD∥AB∥MN,∴△ABE∽△CDE,△ABF∽△MNF,∴CDAB=DEBE,FNFB=MNAB,即1.8AB=1.81.8+BD,1.51.5+2.7-BD=1.5AB,所以AB=3m.
16.3 【解析】 根据题中该正六棱柱的主视图和左视图画出其俯视图,如图所示,连接BC,过点A作AD⊥BC于点D.在△ABC中,AB=AC,∠BAC=120°,所以∠ACD=30°,可得AD=12AC,从而易得2AD+AC=4,所以AC=2,AD=1.在Rt△ACD中,由勾股定理,得CD=3,所以a的值为3.
17.【解析】 主视图和左视图如图所示.
18.【解析】 由主视图和俯视图可知,该几何体是由一个底面直径为20、高为20的圆柱和长、宽、高分别为30,25,40的长方体组成的,所以该几何体的体积为3.14×(20÷2)2×20+25×30×40=36280(mm3).
19.【解析】 (1)路灯O的位置及投影FG如图所示.
(2)如图,过O作OH⊥MG于点H,设DH=xm,
由AB∥CD∥OH,得MBMH=ABOH,NDNH=CDOH,
因为AB=CD,
所以MBMH=NDNH,即1.61.6+2+x=0.60.6+x,
所以x=1.2.
设FG=ym,同理得FGHG=NDNH,
即y2-1.2+y=0.60.6+1.2,
所以y=0.4.
所以EF的影长为0.4m.
20.【解析】 (1)直三棱柱
(2)如图所示.
(3)由题意可得a=h2=202=102(cm),
S表面积=12×(102)2×2+2×102×20+202=(600+4002)(cm2).
21.【解析】 ∵海涛身高1.6米,测得其影长为2.4米,
∴8米高的旗杆DE的影长为12米.
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(米),
∴GM=MH=4米.
如图,设小桥的圆心为O,连接OM,OG,易知OM⊥GH.
设小桥所在圆的半径为r,
∵MN=2米,∴OM=(r-2)米.
在Rt△OGM中,由勾股定理得OG2=OM2+GM2,
∴r2=(r-2)2+42,解得r=5.
答:小桥所在圆的半径为5米.
22.【解析】 (1)木柜露在外面的表面展开图如图所示,
则蚂蚁能够最快到达目的地的可能路径为AC'1或AC1.
(2)路径AC'1的长是42+(4+5)2=97.
路径AC1的长是(4+4)2+52=89.
因为97>89,所以蚂蚁爬过的最短路径的长是89.
(3)如图,过点B1作B1E⊥AC1于点E,易知B1E即点B1到最短路径的距离.
∵∠C1EB1=∠C1A1A=90°,∠EC1B1=∠A1C1A,
∴△B1EC1∽△AA1C1,
∴B1EAA1=B1C1AC1,∴B1E=B1C1AC1×AA1=489×5=208989.
