初中数学苏科版九年级上册1.4用一元二次方程解决问题同步练习(Word版 含解析)
文档属性
| 名称 | 初中数学苏科版九年级上册1.4用一元二次方程解决问题同步练习(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 39.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 11:19:38 | ||
图片预览




文档简介
初中数学苏科版九年级上册第一章1.4用一元二次方程解决问题同步练习
一、选择题
某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗设增加了x行或列,则可列方程为
A.
B.
C.
D.
为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为那么x满足的方程为
A.
18?
B.
18??
C.
??
D.
???
电影我和我的祖国讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把增长率记作x,则方程可以列为
A.
B.
C.
D.
某超市2020年3月份的猪肉价格为60元千克,经过两个月连续两次降价后,5月份的猪肉价格为40元千克,设平均每次降价的百分率为x,则根据题意可列方程为
A.
B.
C.
D.
国家实行“精准扶贫”政策以来,很多贫困人口走上了致富的道路,某地区2017年底有贫困人口50000人,通过社会各界的努力,2019年底贫困人口减少至10000人.设2017年底至2019年底该地区贫因人口的平均下降率为x,根据题意列方程得
A.
B.
C.
D.
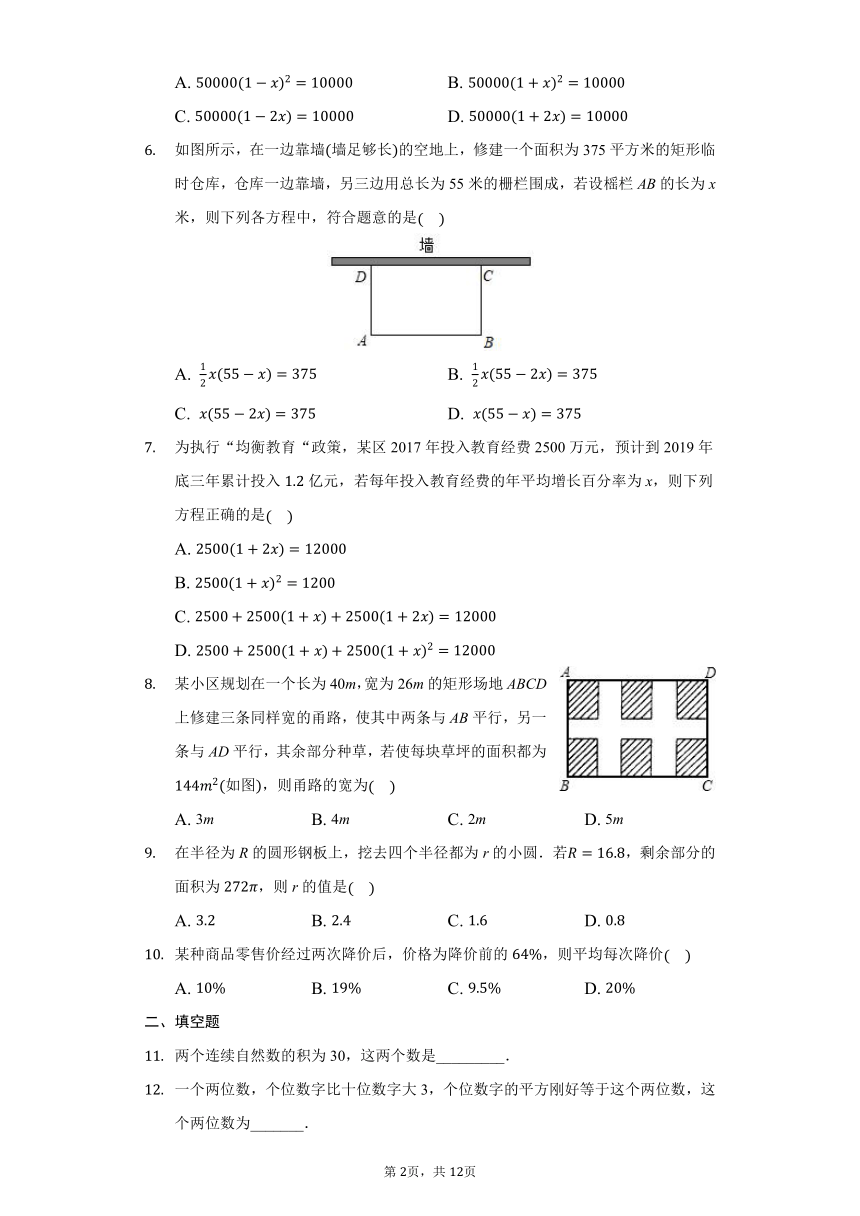
如图所示,在一边靠墙墙足够长的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另三边用总长为55米的栅栏围成,若设榣栏AB的长为x米,则下列各方程中,符合题意的是
A.
B.
C.
D.
为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是
A.
B.
C.
D.
某小区规划在一个长为40m,宽为26m的矩形场地ABCD上修建三条同样宽的甬路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为如图,则甬路的宽为
A.
3m
B.
4m
C.
2m
D.
5m
在半径为R的圆形钢板上,挖去四个半径都为r的小圆.若,剩余部分的面积为,则r的值是
A.
B.
C.
D.
某种商品零售价经过两次降价后,价格为降价前的,则平均每次降价
A.
B.
C.
D.
二、填空题
两个连续自然数的积为30,这两个数是_________.
一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,这个两位数为_______.
在元旦前夕,某通讯公司的每位员工都向本公司的其他员工发出了1条祝贺元旦的短信.已知全公司共发出2450条短信,那么这个公司有员工______人.
有一台电脑中了病毒,经过两轮传染后共有400台电脑中了病毒,那么每轮传染中平均每台传染给______台电脑.
某品牌运动服原来每件售价640元,经过两次降价,售价降低了280元,已知两次降价的百分率相同,则每次降价的百分率为______.
三、解答题
某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?
随着疫情形势稳定向好,“复工复产”成为主旋律.某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架.
求该公司生产A型无人机每月产量的平均增长率;
该公司还生产B型无人机,已知生产1架A型无人机的成本是200元,生产1架B型无人机的成本是300元,现要生产A、B两种型号的无人机共100架,其中A型无人机的数量不超过B型无人机数量的3倍,公司生产A、B两种型号的无人机各多少架时才可能使生产成本最少?
某印刷厂印刷某尺寸的广告纸印刷张数为单位:万张,需按整千张印刷计费,收费规定如下
若:单价为元张;
若:每增加万张所有广告纸每张减少元费用再9折优惠;
若:每增加万张所有广告纸每张减少元费用再8折优惠.
若某客户要印刷广告纸万张则该客户需支付费用______元;
若某客户支付了广告纸费用万元求印刷张数a的值.
因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验;若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗
求出2016年至2018年十一长假期间游客人次的年平均增长率;
为了维护城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天盈利6300元?
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查了一元二次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.设增加了x行或列,根据体操队伍人数不变列出方程即可.
【解答】
解:设增加了x行或列,
根据题意,得.
故选D.
2.【答案】D
【解析】解:设前三个季度用于绿化投资的平均增长率为x,那么依题意得
???.
故选:D.
主要考查增长率问题,一般用增长后的量增长前的量增长率,设这两年绿化投资的年平均增长率为x,根据“第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元”,可得出方程.
本题为平均增长率问题,一般形式为,a为起始时间的有关数量,b为终止时间的有关数量.
3.【答案】D
【解析】解:设平均每天票房的增长率为x,
根据题意得:.
故选:D.
设平均每天票房的增长率为x,根据三天后累计票房收入达10亿元,即可得出关于x的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
4.【答案】B
【解析】解:设平均每次降价的百分率为x,根据题意可列方程:
.
故选:B.
根据关系式:3月份猪肉价格月平均下降率月份猪肉价格,把相关数值代入即可求解.
此题主要考查了由实际问题抽象出一元二次方程,关键是掌握增长率问题的计算公式:变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为.
5.【答案】A
【解析】解:设2017年底至2019年底该地区贫因人口的平均下降率为x,根据题意得:
,
故选:A.
等量关系为:2017年贫困人口下降率年贫困人口,把相关数值代入计算即可.
本题考查由实际问题抽象出一元二次方程,得到2年内变化情况的等量关系是解决本题的关键.
6.【答案】A
【解析】解:设榣栏AB的长为x米,则米,
根据题意可得,,
故选:A.
设榣栏AB的长为x米,根据且可得米,再由长方形的面积公式可得答案.
本题主要考查由实际问题抽象出一元二次方程,在解决实际问题时,要全面、系统地申清问题的已知和未知,以及它们之间的数量关系,找出并全面表示问题的相等关系,设出未知数,用方程表示出已知量与未知量之间的等量关系,即列出一元二次方程.
7.【答案】D
【解析】解:设每年投入教育经费的年平均增长百分率为x,
由题意得,.
故选:D.
设每年投入教育经费的年平均增长百分率为x,根据题意可得,2017年投入教育经费年投入教育经费增长率年投入教育经费增长率亿元,据此列方程.
本题考查了由实际问题抽象出一元二次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.
8.【答案】C
【解析】解:设小路的宽为xm,根据题意得,
整理得,
解得,,
当时不符合题意,故舍去,
所以.
故选:C.
设小路的宽为xm,那么小路所占面积为,于是六块草坪的面积为,根据面积之间的关系可列方程,解方程求解,并根据实际意义进行值的取舍即可确定甬路的宽.
本题考查的是一元二次方程的应用以及矩形面积计算公式,难度一般.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
9.【答案】C
【解析】解:由题意可得,
,
则,
,
,
解得,,舍去,
故选:C.
根据在半径为R的圆形钢板上,挖去四个半径都为r的小圆,可以表示出剩余部分的面积,然后根据,剩余部分的面积为,即可求得r的值.
本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答.
10.【答案】D
【解析】解:设平均每次降价x,根据题意得,
解得或
不符合题意,舍去
平均每次降价.
故选D.
降低后的价格降低前的价格降低率,如果设平均每次降价x,原价是1,则第一次降低后的价格是,那么第二次后的价格是,即可列出方程求解.
本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为当增长时中间的“”号选“”,当降低时中间的“”号选“”
11.【答案】5和6
【解析】
【分析】本题考查一元二次方程的应用,弄清题意,列出相应的方程是解本题的关键.根据连续自然数相差1,设出较小的自然数为x,则较大自然数为,根据两个连续自然数之积是30列出关于x的方程,求出方程的解即可得到x的值,进而确定出连续的两个自然数.
【解答】解:设两个连续的自然数分别为x,,,
由题意得:,即,
因式分解得:,
可得或,
解得:,舍去,
则这两个数是5和6.
故答案为:5和6
12.【答案】25或36
【解析】
【分析】
本题考查了数字问题的数量关系的运用,列一元二次方程的解实际问题的运用,一元二次方程的解法的运用,解答时根据个位数字的平方刚好等于这个两位数建立方程是关键.设十位数字为x,则个位数字为,根据个位数字的平方刚好等于这个两位数建立方程求出其解即可.
【解答】
解:设十位数字为x,则个位数字为,由题意,得
,
解得:,,
个位数字为:5或6,
这个两位数为:25或36.
故答案为25或36.
13.【答案】50
【解析】解:设这个公司有员工x人,则每人需发送条祝贺元旦的短信,
依题意,得:,
解得:,不合题意,舍去.
故答案为:50.
设这个公司有员工x人,则每人需发送条祝贺元旦的短信,根据全公司共发出2450条短信,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
14.【答案】19
【解析】解:设每轮传染中平均每台传染给x台电脑,
依题意,得:,
解得:,不合题意,舍去.
故答案为:19.
设每轮传染中平均每台传染给x台电脑,根据一台电脑中了病毒且经过两轮传染后共有400台电脑中了病毒,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
15.【答案】
【解析】解:设每次降价的百分率为x,
由题意得,.
解得:,或舍去,
答:每次降价的百分比为.
故答案为.
设每次降价的百分率为x,根据降价后的价格降价前的价格降价的百分率,则第一次降价后的价格是,第二次后的价格是,据此即可列方程求解.
本题考查了一元二次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.
16.【答案】解:设与墙垂直的一面为x米,另一面则为米
根据题意得:
整理得:
解得或,
当时,舍去
当时,
长为10米,宽为8米.
设宽为a米,根据题意得:,
,
解得:舍去,,
答:小路的宽为1米.
【解析】设与墙垂直的一面为x米,然后可得另两面则为米,然后利用其面积为80列出方程求解即可;
设小路的宽为a米,利用去掉小路的面积为54平米列出方程求解即可得到答案.
本题考查了一元二次方程的应用,要结合图形求解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
17.【答案】解:设该公司生长A型无人机每月产量的平均增长率为x,根据题意可得:
,
解得:,不合题意舍去,
答:该公司生长A型无人机每月产量的平均增长率为;
设生产A型号无人机a架,则生产B型号无人机架,需要成本为w元,依据题意可得:
,
解得:,
,
,
当a的值增大时,w的值减小,
为整数,
当时,w取最小值,此时,
,
公司生产A型号无人机75架,生产B型号无人机25架成本最小.
【解析】直接利用连续两次平均增长率求法得出等式求出答案;
根据题意求出a的取值范围,再利用一次函数增减性得出答案.
此题主要考查了一元二次方程应用以及一次函数应用,关键是根据题意找到等式两边的平衡条件,找到产量前后变化的平衡关系,列出方程,解答即可.
18.【答案】4725
【解析】解:由题意可得:元;
故答案为:4725;
当时,万元元,
则某客户支付了广告纸费用万元时,总的印刷张数超过2万张,
故,
整理得:,
解得:万不合题意舍去,万,
答:印刷张数a的值为万.
直接利用已知表示出每张广告纸的费用,进而求出总费用;
首先得出a的取值范围,再直接表示出每张广告纸的费用,进而得出等式求出答案.
此题主要考查了一元二次方程的应用,正确表示出每张广告纸的费用是解题关键.
19.【答案】解:可设年平均增长率为x,依题意有
,
解得,舍去.
答:年平均增长率为;
设每碗售价定为y元时,店家才能实现每天利润6300元,依题意有
,
解得,,
每碗售价不得超过20元,
.
答:当每碗售价定为20元时,店家才能实现每天利润6300元.
【解析】可设年平均增长率为x,根据等量关系:2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,列出方程求解即可;
可设每碗售价定为y元时,店家才能实现每天利润6300元,根据利润的等量关系列出方程求解即可.
考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
第2页,共12页
第1页,共12页
一、选择题
某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗设增加了x行或列,则可列方程为
A.
B.
C.
D.
为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为那么x满足的方程为
A.
18?
B.
18??
C.
??
D.
???
电影我和我的祖国讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把增长率记作x,则方程可以列为
A.
B.
C.
D.
某超市2020年3月份的猪肉价格为60元千克,经过两个月连续两次降价后,5月份的猪肉价格为40元千克,设平均每次降价的百分率为x,则根据题意可列方程为
A.
B.
C.
D.
国家实行“精准扶贫”政策以来,很多贫困人口走上了致富的道路,某地区2017年底有贫困人口50000人,通过社会各界的努力,2019年底贫困人口减少至10000人.设2017年底至2019年底该地区贫因人口的平均下降率为x,根据题意列方程得
A.
B.
C.
D.
如图所示,在一边靠墙墙足够长的空地上,修建一个面积为375平方米的矩形临时仓库,仓库一边靠墙,另三边用总长为55米的栅栏围成,若设榣栏AB的长为x米,则下列各方程中,符合题意的是
A.
B.
C.
D.
为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是
A.
B.
C.
D.
某小区规划在一个长为40m,宽为26m的矩形场地ABCD上修建三条同样宽的甬路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为如图,则甬路的宽为
A.
3m
B.
4m
C.
2m
D.
5m
在半径为R的圆形钢板上,挖去四个半径都为r的小圆.若,剩余部分的面积为,则r的值是
A.
B.
C.
D.
某种商品零售价经过两次降价后,价格为降价前的,则平均每次降价
A.
B.
C.
D.
二、填空题
两个连续自然数的积为30,这两个数是_________.
一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,这个两位数为_______.
在元旦前夕,某通讯公司的每位员工都向本公司的其他员工发出了1条祝贺元旦的短信.已知全公司共发出2450条短信,那么这个公司有员工______人.
有一台电脑中了病毒,经过两轮传染后共有400台电脑中了病毒,那么每轮传染中平均每台传染给______台电脑.
某品牌运动服原来每件售价640元,经过两次降价,售价降低了280元,已知两次降价的百分率相同,则每次降价的百分率为______.
三、解答题
某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?
随着疫情形势稳定向好,“复工复产”成为主旋律.某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架.
求该公司生产A型无人机每月产量的平均增长率;
该公司还生产B型无人机,已知生产1架A型无人机的成本是200元,生产1架B型无人机的成本是300元,现要生产A、B两种型号的无人机共100架,其中A型无人机的数量不超过B型无人机数量的3倍,公司生产A、B两种型号的无人机各多少架时才可能使生产成本最少?
某印刷厂印刷某尺寸的广告纸印刷张数为单位:万张,需按整千张印刷计费,收费规定如下
若:单价为元张;
若:每增加万张所有广告纸每张减少元费用再9折优惠;
若:每增加万张所有广告纸每张减少元费用再8折优惠.
若某客户要印刷广告纸万张则该客户需支付费用______元;
若某客户支付了广告纸费用万元求印刷张数a的值.
因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验;若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗
求出2016年至2018年十一长假期间游客人次的年平均增长率;
为了维护城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天盈利6300元?
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查了一元二次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.设增加了x行或列,根据体操队伍人数不变列出方程即可.
【解答】
解:设增加了x行或列,
根据题意,得.
故选D.
2.【答案】D
【解析】解:设前三个季度用于绿化投资的平均增长率为x,那么依题意得
???.
故选:D.
主要考查增长率问题,一般用增长后的量增长前的量增长率,设这两年绿化投资的年平均增长率为x,根据“第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元”,可得出方程.
本题为平均增长率问题,一般形式为,a为起始时间的有关数量,b为终止时间的有关数量.
3.【答案】D
【解析】解:设平均每天票房的增长率为x,
根据题意得:.
故选:D.
设平均每天票房的增长率为x,根据三天后累计票房收入达10亿元,即可得出关于x的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
4.【答案】B
【解析】解:设平均每次降价的百分率为x,根据题意可列方程:
.
故选:B.
根据关系式:3月份猪肉价格月平均下降率月份猪肉价格,把相关数值代入即可求解.
此题主要考查了由实际问题抽象出一元二次方程,关键是掌握增长率问题的计算公式:变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为.
5.【答案】A
【解析】解:设2017年底至2019年底该地区贫因人口的平均下降率为x,根据题意得:
,
故选:A.
等量关系为:2017年贫困人口下降率年贫困人口,把相关数值代入计算即可.
本题考查由实际问题抽象出一元二次方程,得到2年内变化情况的等量关系是解决本题的关键.
6.【答案】A
【解析】解:设榣栏AB的长为x米,则米,
根据题意可得,,
故选:A.
设榣栏AB的长为x米,根据且可得米,再由长方形的面积公式可得答案.
本题主要考查由实际问题抽象出一元二次方程,在解决实际问题时,要全面、系统地申清问题的已知和未知,以及它们之间的数量关系,找出并全面表示问题的相等关系,设出未知数,用方程表示出已知量与未知量之间的等量关系,即列出一元二次方程.
7.【答案】D
【解析】解:设每年投入教育经费的年平均增长百分率为x,
由题意得,.
故选:D.
设每年投入教育经费的年平均增长百分率为x,根据题意可得,2017年投入教育经费年投入教育经费增长率年投入教育经费增长率亿元,据此列方程.
本题考查了由实际问题抽象出一元二次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.
8.【答案】C
【解析】解:设小路的宽为xm,根据题意得,
整理得,
解得,,
当时不符合题意,故舍去,
所以.
故选:C.
设小路的宽为xm,那么小路所占面积为,于是六块草坪的面积为,根据面积之间的关系可列方程,解方程求解,并根据实际意义进行值的取舍即可确定甬路的宽.
本题考查的是一元二次方程的应用以及矩形面积计算公式,难度一般.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
9.【答案】C
【解析】解:由题意可得,
,
则,
,
,
解得,,舍去,
故选:C.
根据在半径为R的圆形钢板上,挖去四个半径都为r的小圆,可以表示出剩余部分的面积,然后根据,剩余部分的面积为,即可求得r的值.
本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答.
10.【答案】D
【解析】解:设平均每次降价x,根据题意得,
解得或
不符合题意,舍去
平均每次降价.
故选D.
降低后的价格降低前的价格降低率,如果设平均每次降价x,原价是1,则第一次降低后的价格是,那么第二次后的价格是,即可列出方程求解.
本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为当增长时中间的“”号选“”,当降低时中间的“”号选“”
11.【答案】5和6
【解析】
【分析】本题考查一元二次方程的应用,弄清题意,列出相应的方程是解本题的关键.根据连续自然数相差1,设出较小的自然数为x,则较大自然数为,根据两个连续自然数之积是30列出关于x的方程,求出方程的解即可得到x的值,进而确定出连续的两个自然数.
【解答】解:设两个连续的自然数分别为x,,,
由题意得:,即,
因式分解得:,
可得或,
解得:,舍去,
则这两个数是5和6.
故答案为:5和6
12.【答案】25或36
【解析】
【分析】
本题考查了数字问题的数量关系的运用,列一元二次方程的解实际问题的运用,一元二次方程的解法的运用,解答时根据个位数字的平方刚好等于这个两位数建立方程是关键.设十位数字为x,则个位数字为,根据个位数字的平方刚好等于这个两位数建立方程求出其解即可.
【解答】
解:设十位数字为x,则个位数字为,由题意,得
,
解得:,,
个位数字为:5或6,
这个两位数为:25或36.
故答案为25或36.
13.【答案】50
【解析】解:设这个公司有员工x人,则每人需发送条祝贺元旦的短信,
依题意,得:,
解得:,不合题意,舍去.
故答案为:50.
设这个公司有员工x人,则每人需发送条祝贺元旦的短信,根据全公司共发出2450条短信,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
14.【答案】19
【解析】解:设每轮传染中平均每台传染给x台电脑,
依题意,得:,
解得:,不合题意,舍去.
故答案为:19.
设每轮传染中平均每台传染给x台电脑,根据一台电脑中了病毒且经过两轮传染后共有400台电脑中了病毒,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
15.【答案】
【解析】解:设每次降价的百分率为x,
由题意得,.
解得:,或舍去,
答:每次降价的百分比为.
故答案为.
设每次降价的百分率为x,根据降价后的价格降价前的价格降价的百分率,则第一次降价后的价格是,第二次后的价格是,据此即可列方程求解.
本题考查了一元二次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程.
16.【答案】解:设与墙垂直的一面为x米,另一面则为米
根据题意得:
整理得:
解得或,
当时,舍去
当时,
长为10米,宽为8米.
设宽为a米,根据题意得:,
,
解得:舍去,,
答:小路的宽为1米.
【解析】设与墙垂直的一面为x米,然后可得另两面则为米,然后利用其面积为80列出方程求解即可;
设小路的宽为a米,利用去掉小路的面积为54平米列出方程求解即可得到答案.
本题考查了一元二次方程的应用,要结合图形求解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.
17.【答案】解:设该公司生长A型无人机每月产量的平均增长率为x,根据题意可得:
,
解得:,不合题意舍去,
答:该公司生长A型无人机每月产量的平均增长率为;
设生产A型号无人机a架,则生产B型号无人机架,需要成本为w元,依据题意可得:
,
解得:,
,
,
当a的值增大时,w的值减小,
为整数,
当时,w取最小值,此时,
,
公司生产A型号无人机75架,生产B型号无人机25架成本最小.
【解析】直接利用连续两次平均增长率求法得出等式求出答案;
根据题意求出a的取值范围,再利用一次函数增减性得出答案.
此题主要考查了一元二次方程应用以及一次函数应用,关键是根据题意找到等式两边的平衡条件,找到产量前后变化的平衡关系,列出方程,解答即可.
18.【答案】4725
【解析】解:由题意可得:元;
故答案为:4725;
当时,万元元,
则某客户支付了广告纸费用万元时,总的印刷张数超过2万张,
故,
整理得:,
解得:万不合题意舍去,万,
答:印刷张数a的值为万.
直接利用已知表示出每张广告纸的费用,进而求出总费用;
首先得出a的取值范围,再直接表示出每张广告纸的费用,进而得出等式求出答案.
此题主要考查了一元二次方程的应用,正确表示出每张广告纸的费用是解题关键.
19.【答案】解:可设年平均增长率为x,依题意有
,
解得,舍去.
答:年平均增长率为;
设每碗售价定为y元时,店家才能实现每天利润6300元,依题意有
,
解得,,
每碗售价不得超过20元,
.
答:当每碗售价定为20元时,店家才能实现每天利润6300元.
【解析】可设年平均增长率为x,根据等量关系:2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,列出方程求解即可;
可设每碗售价定为y元时,店家才能实现每天利润6300元,根据利润的等量关系列出方程求解即可.
考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
第2页,共12页
第1页,共12页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
