人教版数学 八年级 上册 13.2 画轴对称图形 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版数学 八年级 上册 13.2 画轴对称图形 同步练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 222.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览




文档简介
画轴对称图形同步练习
一、选择题
如图,把ABC经过一定的变换得到,如果上点P的坐标为,那么这个点在中的对应点的坐标为
A.
B.
C.
D.
点A和点关于x轴对称,则A,B两点间的距离是
A.
4
B.
5
C.
6
D.
10
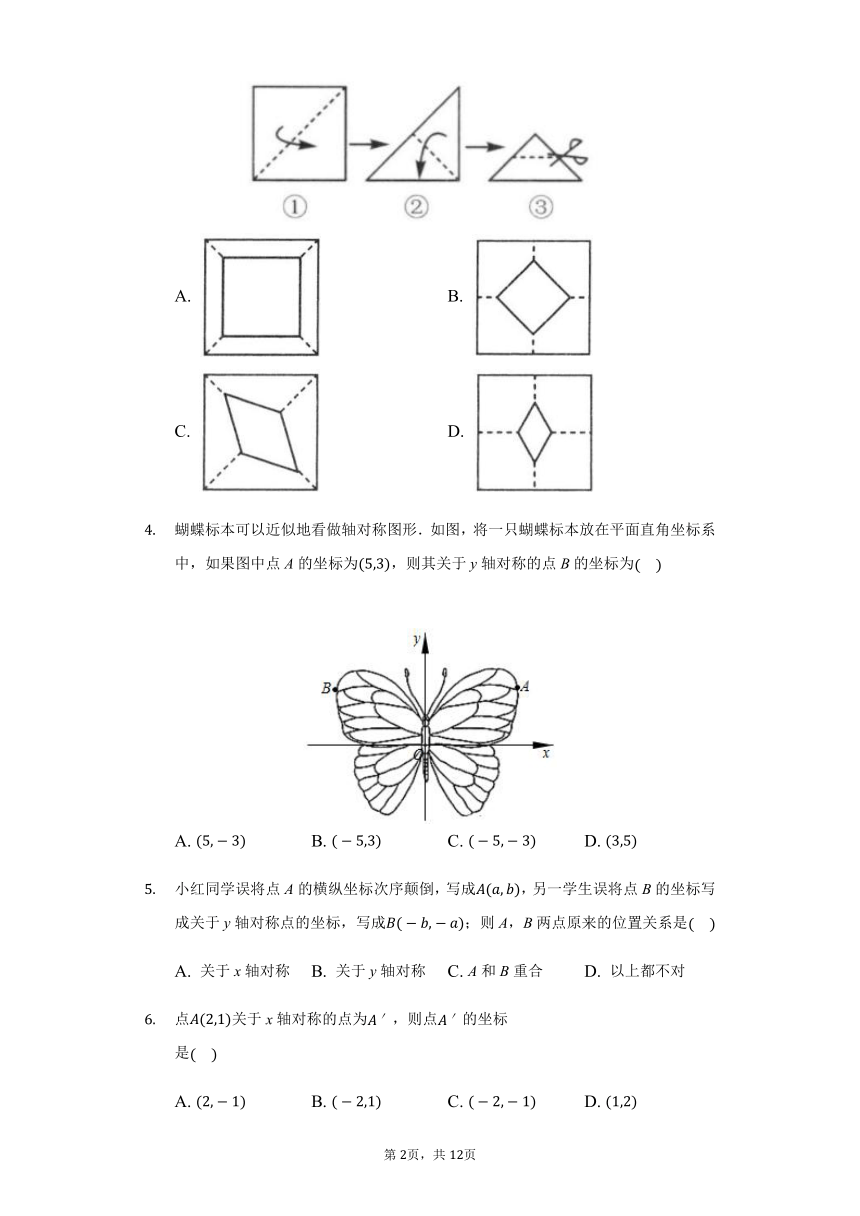
将一张正方形纸片按如图步骤,沿虚线对折两次,然后沿中平行于底边的虚线剪去一个角,展开铺平后的图形是?
A.
B.
C.
D.
蝴蝶标本可以近似地看做轴对称图形.如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为,则其关于y轴对称的点B的坐标为
A.
B.
C.
D.
小红同学误将点A的横纵坐标次序颠倒,写成,另一学生误将点B的坐标写成关于y轴对称点的坐标,写成;则A,B两点原来的位置关系是
A.
关于x轴对称
B.
关于y轴对称
C.
A和B重合
D.
以上都不对
点关于x轴对称的点为,则点的坐标是
A.
B.
C.
D.
如图,将的三个顶点坐标的横坐标都乘以,并保持纵坐标不变,则所得图形与原图形的关系是
A.
关于x轴对称
B.
关于y轴对称
C.
将原图形沿x轴的负方向平移了1个单位
D.
将原图形沿y轴的负方向平移了1个单位
已知点A与点B关于y轴对称,若点A的坐标为,点B的坐标为,则
A.
B.
3
C.
D.
1
在平面直角坐标系中,点关于x轴对称点为,则的值为
A.
B.
1
C.
D.
2
在平面直角坐标系中,将点向右平移3个单位得到点,则点关于x轴的对称点的坐标为
A.
B.
C.
D.
如图,已知点A的坐标为,过点A作x轴的垂线交x轴于点B,连接AO,现将沿AO折叠,点B落在第一象限的处,则直线与x轴的交点D的坐标为
A.
B.
C.
D.
已知A,B两点的坐标分别是和,则下面四个结论:
、B关于x轴对称;、B关于y轴对称;点在第二象限,B点在第一象限;、B之间的距离为其中正确的有
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
已知点关于x轴的对称点是第三象限内的整点横、纵坐标都为整数的点,称为整点,则点的坐标是__________.
请在如图所示的这一组图形中找出它们所蕴含的内在规律,然后在横线上填上恰当的图形.
平面直角坐标系中的点关于x轴的对称点在第四象限,则m的取值范围为______
.
已知点,关于x轴对称,则mn的值为______.
三、解答题(本大题共3小题,共24.0分)
已知点,,,
在平面直角坐标系中,描出各点并依次连接各点得到四边形OCED.
按要求绘制下列图形,并说明发生了哪些变化?
横坐标不变,纵坐标都乘以;
纵坐标不变,横坐标都乘以.
如图在平面直角坐标系中,各顶点的坐标分别为:,,.
在图中作使和关于x轴对称;
写出点,,的坐标;
求的面积.
如图,网格中的与为轴对称图形.
利用网格线作出与的对称轴l;
结合所画图形,在直线l上画出点P,使最小;
如果每一个小正方形的边长为1,请直接写出的面积______.
答案和解析
1.【答案】B
【解答】
解:把向上平移2个单位,再关于y轴对称可得到,
点的对应点的坐标为.
故选:B.
2.【答案】C
【解答】解:点A和点关于x轴对称,
点A的坐标为,
.
故选C.
3.【答案】A
【解答】
解:由于得到的图形的中间是正方形,且顶点在原来的正方形的对角线上,
故选:A.
4.【答案】B
【解答】
解:,B关于y轴对称,,
,
故选:B.
5.【答案】A
【解答】
解:小红同学误将点A的横纵坐标次序颠倒,写成,
点的正确坐标为,
另一学生误将点B的坐标写成关于y轴对称点的坐标,写成,
点的正确坐标为,
,B两点原来的位置关系是关于x轴对称,
故选:A.
6.【答案】A
【解析】解:根据轴对称的性质,得点关于x轴对称点的坐标是,
故选:A.
7.【答案】B
【解析】解:将的三个顶点坐标的横坐标乘以,纵坐标不变,得
横坐标互为相反数,纵坐标相等,得
所得图形与原图形的关系是关于y轴对称,
8.【答案】B
【解析】解:点和关于y轴对称,
,,
.
9.【答案】C
【解析】解:点与点关于x轴对称,
,,
.
10.【答案】A
【解析】解:将点向右平移3个单位得到点,
点的坐标是,
点关于x轴的对称点的坐标是.
11.【答案】D
【解析】解:根据翻折可知:
,,,,
轴,
轴,
,
,
,
设,则,
在中,根据勾股定理,得
,即,
解得,
,
,
设直线AD解析式为,
将,代入,得
,,解得,
直线AD解析式为,
当时,,
点的坐标为.
12.【答案】B
【解析】解:,B两点的坐标分别是和,纵坐标不变,横坐标互为相反数,
、B两点关于y轴对称,
故错误,正确;
点A在第二象限,点B在第一象限,故正确;
A、B之间的距离为,
故错误,
正确的有2个,
13.【答案】
【解答】
解:是第三象限内的整点,
,解得;
和都必须为整数,
必须为整数,
,
,解得;
点的坐标是.
与关于x轴对称,可得到点的坐标是.
14.【答案】
【解答】
解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是的数字,所以画一个轴对称图形且数字为6即可.
如图所示:
故答案为.
15.【答案】
【解析】解:点关于x轴对称的点的坐标为,
在第四象限,
,解得,
的取值范围为.
故答案为.
先根据x轴对称的点的坐标特点得到点关于x轴对称的点的坐标为,然后根据第四象限点的坐标特点得到,再解不等式组即可.
16.【答案】3
【解析】解:点,关于x轴对称,
,,
,
故答案为:3.
17.【答案】解:四边形OCED如图所示;
四边形如图所示;
四边形如图所示.
【解析】根据平面直角坐标系找出各点的位置,然后顺次连接即可;
根据网格结构找出点C、E、D横坐标不变,纵坐标都乘以的对应点、、的位置,再与点O顺次连接即可;
根据网格结构找出点C、E、D纵坐标不变,横坐标都乘以的对应点、、的位置,再与点O顺次连接即可.
18.【答案】解:如图所示;
由得点的坐标为,点的坐标为,点的坐标为;
.
19.【答案】解:如图所示,直线l即为所求.
如图所示,点P即为所求;
.
【解析】
解:见答案;
见答案;
的面积,
故答案为:3.
第2页,共2页
第1页,共1页
一、选择题
如图,把ABC经过一定的变换得到,如果上点P的坐标为,那么这个点在中的对应点的坐标为
A.
B.
C.
D.
点A和点关于x轴对称,则A,B两点间的距离是
A.
4
B.
5
C.
6
D.
10
将一张正方形纸片按如图步骤,沿虚线对折两次,然后沿中平行于底边的虚线剪去一个角,展开铺平后的图形是?
A.
B.
C.
D.
蝴蝶标本可以近似地看做轴对称图形.如图,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为,则其关于y轴对称的点B的坐标为
A.
B.
C.
D.
小红同学误将点A的横纵坐标次序颠倒,写成,另一学生误将点B的坐标写成关于y轴对称点的坐标,写成;则A,B两点原来的位置关系是
A.
关于x轴对称
B.
关于y轴对称
C.
A和B重合
D.
以上都不对
点关于x轴对称的点为,则点的坐标是
A.
B.
C.
D.
如图,将的三个顶点坐标的横坐标都乘以,并保持纵坐标不变,则所得图形与原图形的关系是
A.
关于x轴对称
B.
关于y轴对称
C.
将原图形沿x轴的负方向平移了1个单位
D.
将原图形沿y轴的负方向平移了1个单位
已知点A与点B关于y轴对称,若点A的坐标为,点B的坐标为,则
A.
B.
3
C.
D.
1
在平面直角坐标系中,点关于x轴对称点为,则的值为
A.
B.
1
C.
D.
2
在平面直角坐标系中,将点向右平移3个单位得到点,则点关于x轴的对称点的坐标为
A.
B.
C.
D.
如图,已知点A的坐标为,过点A作x轴的垂线交x轴于点B,连接AO,现将沿AO折叠,点B落在第一象限的处,则直线与x轴的交点D的坐标为
A.
B.
C.
D.
已知A,B两点的坐标分别是和,则下面四个结论:
、B关于x轴对称;、B关于y轴对称;点在第二象限,B点在第一象限;、B之间的距离为其中正确的有
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
已知点关于x轴的对称点是第三象限内的整点横、纵坐标都为整数的点,称为整点,则点的坐标是__________.
请在如图所示的这一组图形中找出它们所蕴含的内在规律,然后在横线上填上恰当的图形.
平面直角坐标系中的点关于x轴的对称点在第四象限,则m的取值范围为______
.
已知点,关于x轴对称,则mn的值为______.
三、解答题(本大题共3小题,共24.0分)
已知点,,,
在平面直角坐标系中,描出各点并依次连接各点得到四边形OCED.
按要求绘制下列图形,并说明发生了哪些变化?
横坐标不变,纵坐标都乘以;
纵坐标不变,横坐标都乘以.
如图在平面直角坐标系中,各顶点的坐标分别为:,,.
在图中作使和关于x轴对称;
写出点,,的坐标;
求的面积.
如图,网格中的与为轴对称图形.
利用网格线作出与的对称轴l;
结合所画图形,在直线l上画出点P,使最小;
如果每一个小正方形的边长为1,请直接写出的面积______.
答案和解析
1.【答案】B
【解答】
解:把向上平移2个单位,再关于y轴对称可得到,
点的对应点的坐标为.
故选:B.
2.【答案】C
【解答】解:点A和点关于x轴对称,
点A的坐标为,
.
故选C.
3.【答案】A
【解答】
解:由于得到的图形的中间是正方形,且顶点在原来的正方形的对角线上,
故选:A.
4.【答案】B
【解答】
解:,B关于y轴对称,,
,
故选:B.
5.【答案】A
【解答】
解:小红同学误将点A的横纵坐标次序颠倒,写成,
点的正确坐标为,
另一学生误将点B的坐标写成关于y轴对称点的坐标,写成,
点的正确坐标为,
,B两点原来的位置关系是关于x轴对称,
故选:A.
6.【答案】A
【解析】解:根据轴对称的性质,得点关于x轴对称点的坐标是,
故选:A.
7.【答案】B
【解析】解:将的三个顶点坐标的横坐标乘以,纵坐标不变,得
横坐标互为相反数,纵坐标相等,得
所得图形与原图形的关系是关于y轴对称,
8.【答案】B
【解析】解:点和关于y轴对称,
,,
.
9.【答案】C
【解析】解:点与点关于x轴对称,
,,
.
10.【答案】A
【解析】解:将点向右平移3个单位得到点,
点的坐标是,
点关于x轴的对称点的坐标是.
11.【答案】D
【解析】解:根据翻折可知:
,,,,
轴,
轴,
,
,
,
设,则,
在中,根据勾股定理,得
,即,
解得,
,
,
设直线AD解析式为,
将,代入,得
,,解得,
直线AD解析式为,
当时,,
点的坐标为.
12.【答案】B
【解析】解:,B两点的坐标分别是和,纵坐标不变,横坐标互为相反数,
、B两点关于y轴对称,
故错误,正确;
点A在第二象限,点B在第一象限,故正确;
A、B之间的距离为,
故错误,
正确的有2个,
13.【答案】
【解答】
解:是第三象限内的整点,
,解得;
和都必须为整数,
必须为整数,
,
,解得;
点的坐标是.
与关于x轴对称,可得到点的坐标是.
14.【答案】
【解答】
解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是的数字,所以画一个轴对称图形且数字为6即可.
如图所示:
故答案为.
15.【答案】
【解析】解:点关于x轴对称的点的坐标为,
在第四象限,
,解得,
的取值范围为.
故答案为.
先根据x轴对称的点的坐标特点得到点关于x轴对称的点的坐标为,然后根据第四象限点的坐标特点得到,再解不等式组即可.
16.【答案】3
【解析】解:点,关于x轴对称,
,,
,
故答案为:3.
17.【答案】解:四边形OCED如图所示;
四边形如图所示;
四边形如图所示.
【解析】根据平面直角坐标系找出各点的位置,然后顺次连接即可;
根据网格结构找出点C、E、D横坐标不变,纵坐标都乘以的对应点、、的位置,再与点O顺次连接即可;
根据网格结构找出点C、E、D纵坐标不变,横坐标都乘以的对应点、、的位置,再与点O顺次连接即可.
18.【答案】解:如图所示;
由得点的坐标为,点的坐标为,点的坐标为;
.
19.【答案】解:如图所示,直线l即为所求.
如图所示,点P即为所求;
.
【解析】
解:见答案;
见答案;
的面积,
故答案为:3.
第2页,共2页
第1页,共1页
