共点力作用下物体的平衡课件33张PPT
文档属性
| 名称 | 共点力作用下物体的平衡课件33张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 699.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-03 16:17:21 | ||
图片预览





文档简介
共点力作用下物体的平衡
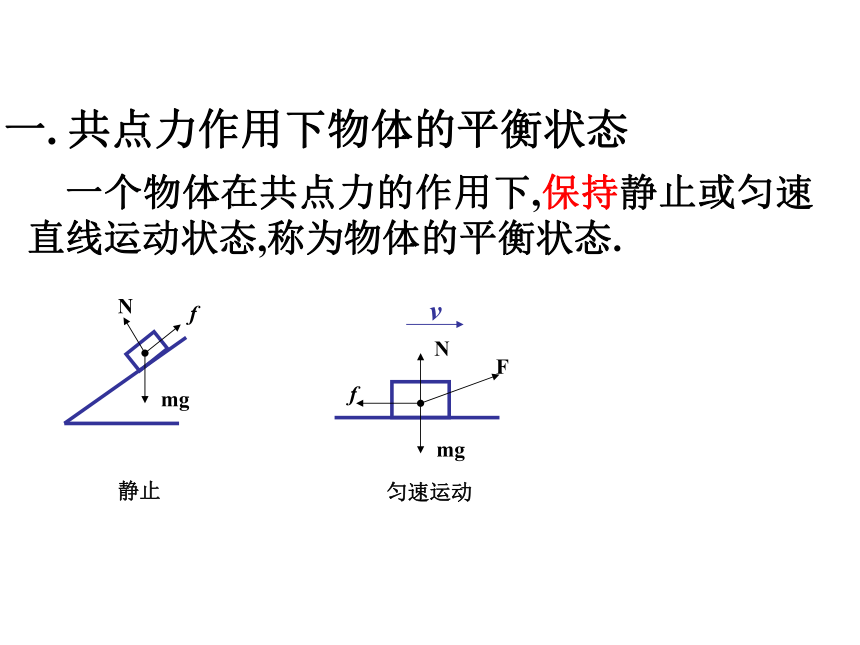
一. 共点力作用下物体的平衡状态
一个物体在共点力的作用下,保持静止或匀速直线运动状态,称为物体的平衡状态.
mg
N
f
mg
N
F
f
v
静止
匀速运动
二.共点力作用下物体的平衡条件
1. 理论推导
在共点力作用下物体平衡条件是合力为零.即:
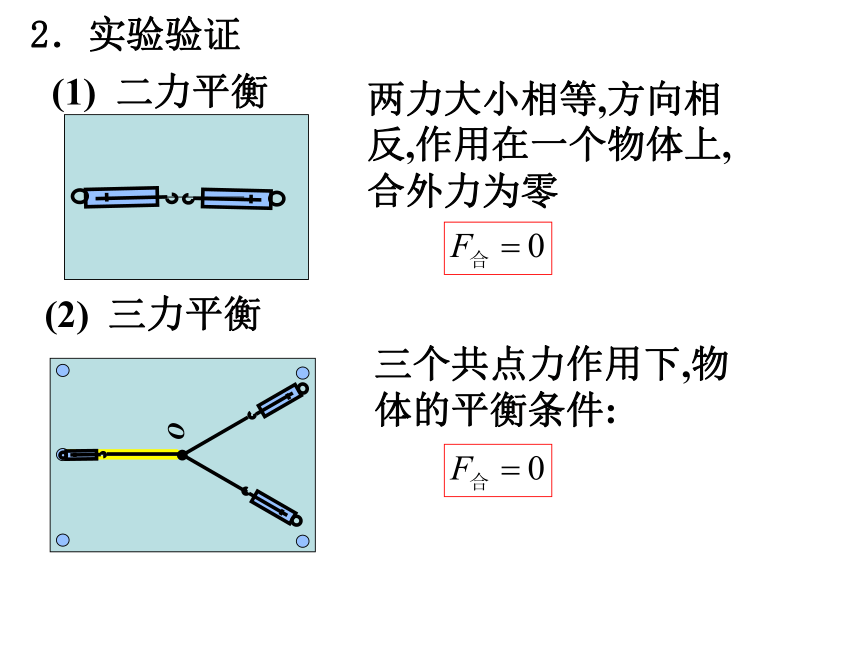
2.实验验证
(1) 二力平衡
两力大小相等,方向相反,作用在一个物体上,合外力为零
O
(2) 三力平衡
三个共点力作用下,物体的平衡条件:
二力平衡
两力是一对平衡力
三力平衡
o
N
f
mg
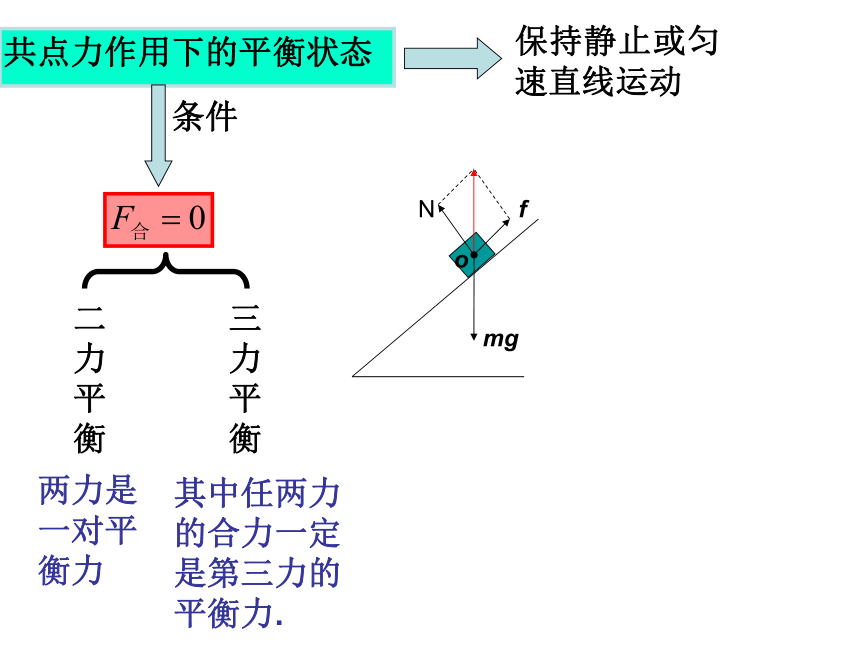
共点力作用下的平衡状态
保持静止或匀速直线运动
其中任两力的合力一定是第三力的平衡力.
条件
注意:
物体在多个共点力作用下处于平衡状态 ,其中任一个力必是其余几个力合力的平衡力.
F2
F3
F1
O
F4
F234
拓展
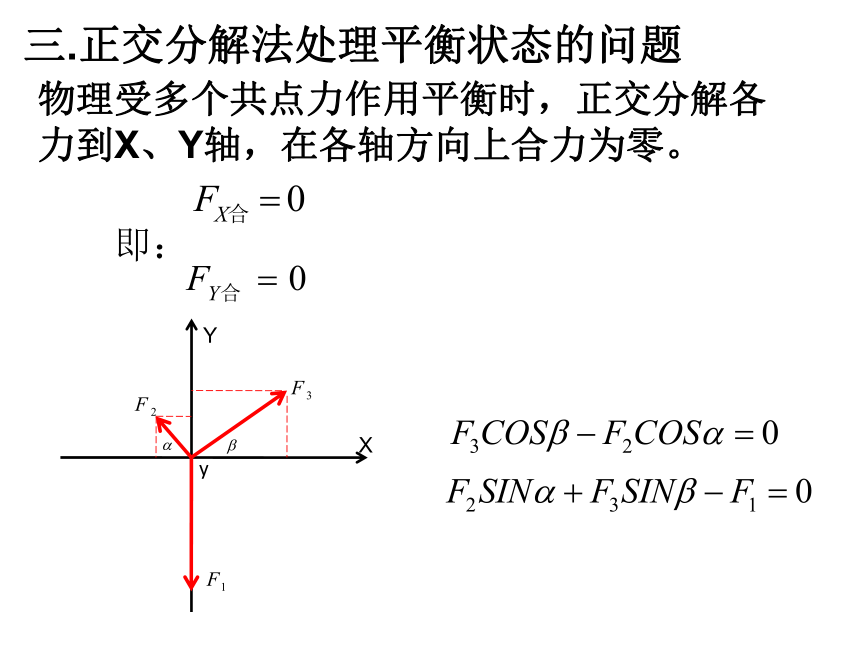
三.正交分解法处理平衡状态的问题
物理受多个共点力作用平衡时,正交分解各力到X、Y轴,在各轴方向上合力为零。
即:
y
Y
X
N
G
f
N
Y
X
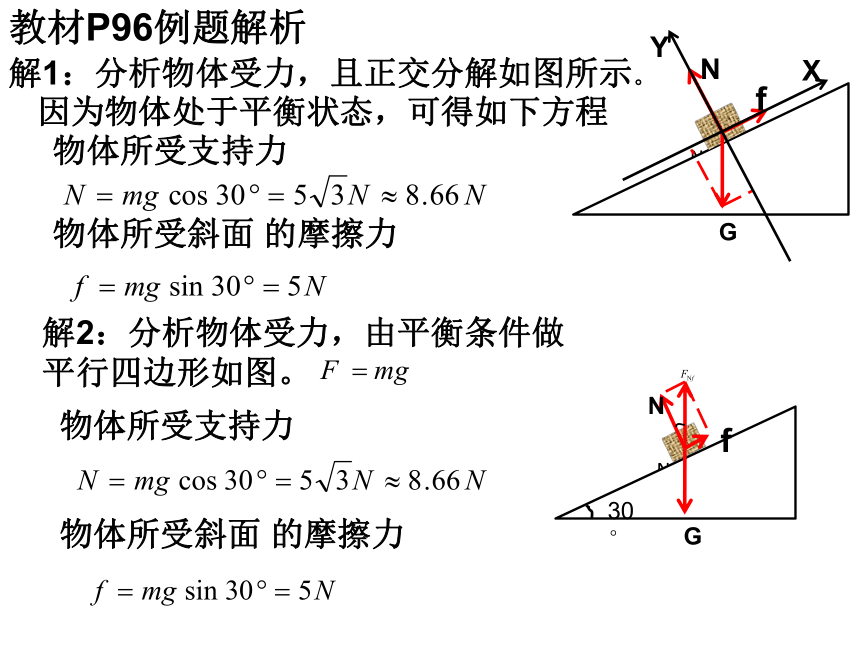
解1:分析物体受力,且正交分解如图所示。
因为物体处于平衡状态,可得如下方程
物体所受支持力
物体所受斜面 的摩擦力
教材P96例题解析
解2:分析物体受力,由平衡条件做平行四边形如图。
物体所受支持力
物体所受斜面 的摩擦力
N
G
f
N
30 °
一、.正交分解法
例1、质量为m的小孩坐在质量为M的滑梯上,滑梯位于粗糙的水平地面上。为了防止小孩下滑,大人用一个水平力F推着小孩(如图)。当大人的推力F逐渐加大的过程中,小孩和滑梯都保持静止状态。在此过程中,下列判断中正确的是
A.滑梯对小孩的摩擦力先减小后增大
B.小孩受到的摩擦力逐渐增大
C.地面对滑梯的摩擦力逐渐减小
D.地面对滑梯的摩擦力逐渐增大
F
m
M
分析与解答:
我们选小孩为研究对象。小孩受推力、重力、弹力还有斜面对小孩的静摩擦力。由于静摩擦力具有被动性,方向和大小与所受的其它力有关,所以我们可以先不画上,但我们知道它的方向在x轴上。
F
m
M
θ
G
N
X
y
当:Fcosθ f向上,减小
Fcosθ=mgsinθ时,
f=0
Fcosθ>mgsinθ时,
f向下,增大
所以:滑梯对小孩的静摩擦力是先减小,后增大。
本题的答案是:A、D
F
m
M
θ
G
N
X
y
二、.图解法
例1:半圆形支架BAD。
两细绳OA和OB 结于O,
下悬重为G的物体,使
OA绳固定不动。将OB
绳的B端沿半圆支架从水平位置逐渐移至竖直的位置C的过程中,(如图所示)分析OA绳和OB绳所受力的大小如何变化?
分析与解答:
以节点O为研究对象,受三个力的作用:G、FA、FB的作用,三个力构成一个封闭三角形。G的大小和方向都不变,FA的方向不变,大小可以改变。当改变FB的方向时,可以看出:FA逐渐减小,FB先减小,后增大。
G
FB
FA
FB1
FB2
例2:如图所示,保持θ不变,将C点向上移,则CO绳的拉力将
A.逐渐减小
B.逐渐增大
C.先减小后增大
D.先增大后减小
θ
B
C
O
G
G
FB
FC1
FC2
FC
答案:C
形似而本质不同的问题
例1:如图所示,质量不计的定滑轮通过轻绳挂在B点,另一轻绳一端系一重物C,绕过滑轮后另一端固定在墙上A点。先将B点或左或右移动一下,若移动过程中OA段绳子始终水平,且不计一切摩擦,则悬点B受拉力T的情况应是
A.B左移时,T增大
B.B右移时,T增大
C.无论B左移右移,T变大
D. 无论B左移右移,T不变
B
A
O
C
分析与解答:
BD绳的拉力大小等于AO和CO绳的合力,由于同一条轻绳上的张力处处相等,因此,AO和BO绳的合力总是向斜下方,与水平成450角,所以当B点移动时BO绳的方向不变,力的大小也不变。
B
A
O
C
G
G
F合
例3:如图所示,质量为m的物体用一轻绳挂在水平轻杆BC的C端,C点由轻绳AC系住,已知AC、BC夹角为θ,轻绳AC上的张力大小为 ,轻杆BC上的压力大小为 .
FB
mg
θ
分析与解答:
FA
例4:如图所示,横杆AB水平插在墙内,它的B端有一个光滑的定滑轮,细绳一端固定于C点,绳跨过滑轮,另一端悬挂一重10N的物体,绳与横梁夹角为300,求定滑轮受到绳对它作用力的大小和方向。
B
300
A
C
分析与解答:
由于同一根绳上张力处处相等,所以合力为10N.
10N
10N
1200
10N
三、相似三角形、
封闭三角形法:
例题:1.如图所示,物重50N,轻杆AB长1.5m.轻杆BC长2.0m,AC间的距离为1.0m。求AB和BC杆所受的力分别为多大。
解:(体会利用相似三角
形、封闭三角形法来解题
的方法和技巧)
A
B
C
N
A
B
C
T
F合=mg
解此题可以用力的合成的方法,如右上图,三角形△CBA与△BNF合相似,得:
∴
还可以根据封闭三角形的方法,画出如右下图,同样用相似三角形得出以上结果。
N
mg
T
N
A
B
C
T
四、临界问题
例1:如图所示,物体A质量m=2kg,用两根轻绳B、C连结竖直墙上,在物体A上加以恒力F,若图中夹角θ=600,要使两绳都能绷直,求恒力F的大小。
θ
A
B
C
θ
分析与解答:
解决临界问题,最重要的是首先要找出在那儿存在临界现象,要尽快的找出临界现象,就要用到极限的方法,把静的问题,让它“动”起来。
在本题中,设想F很小趋近于零时,AB绳肯定是松的,当随着F的增大,AC绳与竖直方向的夹角逐渐变大,当绳AC刚刚拉直时,是F的最小值。
2Fsinθ=mg 即: 2Fsin600=20
θ
A
B
C
θ
F
FC
mg
在此基础上,F继续增大,当增大到一定程度时,AC绳就会变松,当绳AC的拉力变为零时,F最大。Fsin600=mg
F=mg/sin600
θ
A
B
C
θ
F
FB
答案:11.55N≤F≤23.09N
mg
一. 共点力作用下物体的平衡状态
一个物体在共点力的作用下,保持静止或匀速直线运动状态,称为物体的平衡状态.
mg
N
f
mg
N
F
f
v
静止
匀速运动
二.共点力作用下物体的平衡条件
1. 理论推导
在共点力作用下物体平衡条件是合力为零.即:
2.实验验证
(1) 二力平衡
两力大小相等,方向相反,作用在一个物体上,合外力为零
O
(2) 三力平衡
三个共点力作用下,物体的平衡条件:
二力平衡
两力是一对平衡力
三力平衡
o
N
f
mg
共点力作用下的平衡状态
保持静止或匀速直线运动
其中任两力的合力一定是第三力的平衡力.
条件
注意:
物体在多个共点力作用下处于平衡状态 ,其中任一个力必是其余几个力合力的平衡力.
F2
F3
F1
O
F4
F234
拓展
三.正交分解法处理平衡状态的问题
物理受多个共点力作用平衡时,正交分解各力到X、Y轴,在各轴方向上合力为零。
即:
y
Y
X
N
G
f
N
Y
X
解1:分析物体受力,且正交分解如图所示。
因为物体处于平衡状态,可得如下方程
物体所受支持力
物体所受斜面 的摩擦力
教材P96例题解析
解2:分析物体受力,由平衡条件做平行四边形如图。
物体所受支持力
物体所受斜面 的摩擦力
N
G
f
N
30 °
一、.正交分解法
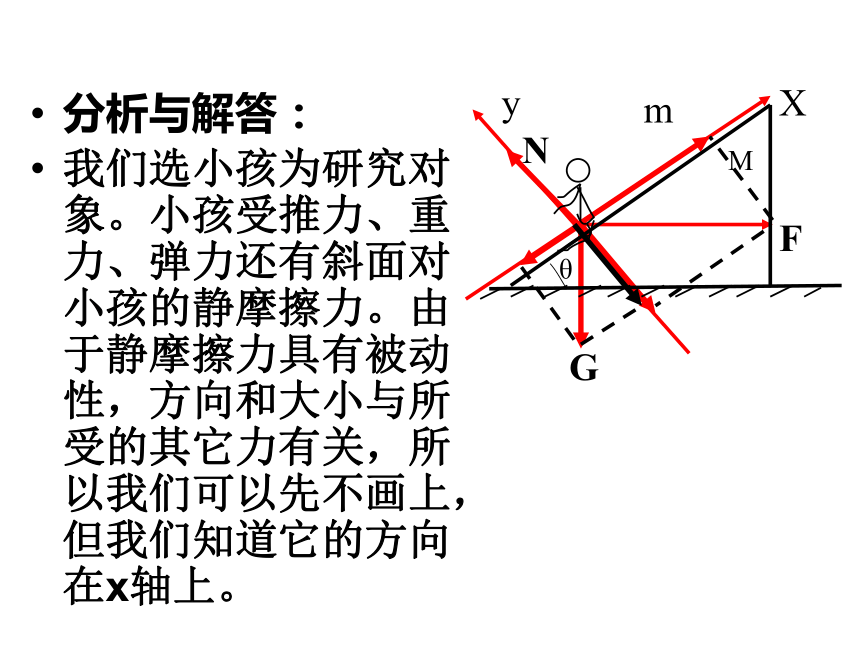
例1、质量为m的小孩坐在质量为M的滑梯上,滑梯位于粗糙的水平地面上。为了防止小孩下滑,大人用一个水平力F推着小孩(如图)。当大人的推力F逐渐加大的过程中,小孩和滑梯都保持静止状态。在此过程中,下列判断中正确的是
A.滑梯对小孩的摩擦力先减小后增大
B.小孩受到的摩擦力逐渐增大
C.地面对滑梯的摩擦力逐渐减小
D.地面对滑梯的摩擦力逐渐增大
F
m
M
分析与解答:
我们选小孩为研究对象。小孩受推力、重力、弹力还有斜面对小孩的静摩擦力。由于静摩擦力具有被动性,方向和大小与所受的其它力有关,所以我们可以先不画上,但我们知道它的方向在x轴上。
F
m
M
θ
G
N
X
y
当:Fcosθ
Fcosθ=mgsinθ时,
f=0
Fcosθ>mgsinθ时,
f向下,增大
所以:滑梯对小孩的静摩擦力是先减小,后增大。
本题的答案是:A、D
F
m
M
θ
G
N
X
y
二、.图解法
例1:半圆形支架BAD。
两细绳OA和OB 结于O,
下悬重为G的物体,使
OA绳固定不动。将OB
绳的B端沿半圆支架从水平位置逐渐移至竖直的位置C的过程中,(如图所示)分析OA绳和OB绳所受力的大小如何变化?
分析与解答:
以节点O为研究对象,受三个力的作用:G、FA、FB的作用,三个力构成一个封闭三角形。G的大小和方向都不变,FA的方向不变,大小可以改变。当改变FB的方向时,可以看出:FA逐渐减小,FB先减小,后增大。
G
FB
FA
FB1
FB2
例2:如图所示,保持θ不变,将C点向上移,则CO绳的拉力将
A.逐渐减小
B.逐渐增大
C.先减小后增大
D.先增大后减小
θ
B
C
O
G
G
FB
FC1
FC2
FC
答案:C
形似而本质不同的问题
例1:如图所示,质量不计的定滑轮通过轻绳挂在B点,另一轻绳一端系一重物C,绕过滑轮后另一端固定在墙上A点。先将B点或左或右移动一下,若移动过程中OA段绳子始终水平,且不计一切摩擦,则悬点B受拉力T的情况应是
A.B左移时,T增大
B.B右移时,T增大
C.无论B左移右移,T变大
D. 无论B左移右移,T不变
B
A
O
C
分析与解答:
BD绳的拉力大小等于AO和CO绳的合力,由于同一条轻绳上的张力处处相等,因此,AO和BO绳的合力总是向斜下方,与水平成450角,所以当B点移动时BO绳的方向不变,力的大小也不变。
B
A
O
C
G
G
F合
例3:如图所示,质量为m的物体用一轻绳挂在水平轻杆BC的C端,C点由轻绳AC系住,已知AC、BC夹角为θ,轻绳AC上的张力大小为 ,轻杆BC上的压力大小为 .
FB
mg
θ
分析与解答:
FA
例4:如图所示,横杆AB水平插在墙内,它的B端有一个光滑的定滑轮,细绳一端固定于C点,绳跨过滑轮,另一端悬挂一重10N的物体,绳与横梁夹角为300,求定滑轮受到绳对它作用力的大小和方向。
B
300
A
C
分析与解答:
由于同一根绳上张力处处相等,所以合力为10N.
10N
10N
1200
10N
三、相似三角形、
封闭三角形法:
例题:1.如图所示,物重50N,轻杆AB长1.5m.轻杆BC长2.0m,AC间的距离为1.0m。求AB和BC杆所受的力分别为多大。
解:(体会利用相似三角
形、封闭三角形法来解题
的方法和技巧)
A
B
C
N
A
B
C
T
F合=mg
解此题可以用力的合成的方法,如右上图,三角形△CBA与△BNF合相似,得:
∴
还可以根据封闭三角形的方法,画出如右下图,同样用相似三角形得出以上结果。
N
mg
T
N
A
B
C
T
四、临界问题
例1:如图所示,物体A质量m=2kg,用两根轻绳B、C连结竖直墙上,在物体A上加以恒力F,若图中夹角θ=600,要使两绳都能绷直,求恒力F的大小。
θ
A
B
C
θ
分析与解答:
解决临界问题,最重要的是首先要找出在那儿存在临界现象,要尽快的找出临界现象,就要用到极限的方法,把静的问题,让它“动”起来。
在本题中,设想F很小趋近于零时,AB绳肯定是松的,当随着F的增大,AC绳与竖直方向的夹角逐渐变大,当绳AC刚刚拉直时,是F的最小值。
2Fsinθ=mg 即: 2Fsin600=20
θ
A
B
C
θ
F
FC
mg
在此基础上,F继续增大,当增大到一定程度时,AC绳就会变松,当绳AC的拉力变为零时,F最大。Fsin600=mg
F=mg/sin600
θ
A
B
C
θ
F
FB
答案:11.55N≤F≤23.09N
mg
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
