苏科版九年级数学下册 7.2 正弦余弦(2)同步练习(含答案)
文档属性
| 名称 | 苏科版九年级数学下册 7.2 正弦余弦(2)同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 19:16:07 | ||
图片预览

文档简介
7.2正弦余弦(2)
1.∠α的补角是120°,则∠α=______,sinα=______.
2.已知△中,,3cosB=2,AC=,则AB= .
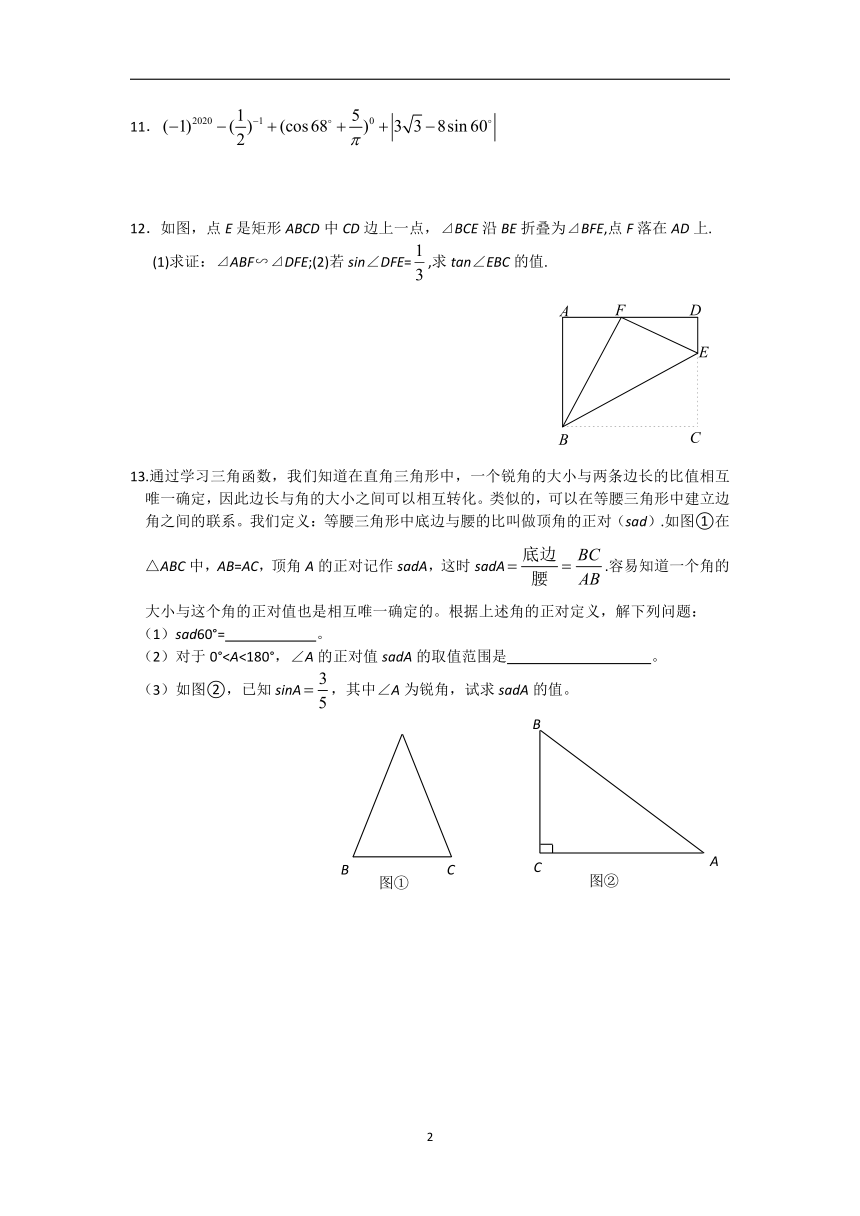
3.如图,△ABC的顶点都在方格纸的格点上,则sinA=_______.
(第3题) (第5题) (第6题)
4.菱形的两条对角线长分别是8和6,较短的一条对角线与菱形的一边的夹角为,则
sin=________,cos=________,tan=__________。
5.如图,将边长为的等边折叠,折痕为,点与点重合,和分别交于点、,,垂足为,.设的面积为,则重叠部分的面积为 .(用含的式子表示)
6.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=.则下列关系式中不成立的是( )
(A)tanA·cotA=1 (B)sinA=tanA·cosA (C)cosA=cotA·sinA (D)tan2A+cot2A=1
7.已知为锐角且=则等于( )
A. B. C. D.
8.在△ABC中,∠A=120°,AB=4,AC=2,则的值是
9.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1交AC于点D,如果AD=,则△ABC的周长等于 .
10. 先化简再求值:,其中.
11.
12.如图,点E是矩形ABCD中CD边上一点,⊿BCE沿BE折叠为⊿BFE,点F落在AD上.
(1)求证:⊿ABF∽⊿DFE;(2)若sin∠DFE=,求tan∠EBC的值.
13.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
(1)sad60°= 。
(2)对于0°(3)如图②,已知sinA,其中∠A为锐角,试求sadA的值。
参考答案:
1.600,;2.6;3.;4.;5.;6.D;7.B;8.;9.;
10.;11.;
12. 解:(1)∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE,
(2)在Rt△DEF中,sin∠DFE==,
∴设DE=a,EF=3a,DF==2a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
∵△ABF∽△DFE,∴=,∴tan∠EBF==,
tan∠EBC=tan∠EBF=.
变式:如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE.
(2)若sin∠DFE=,求tan∠EBC的值.
(3)设=k,是否存在k的值,使△ABF与△BFE相似?若存在谋求出k的值;若不存在,请说明理由.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE;
(2)解:在Rt△DEF中,sin∠DFE==,
∴设DE=2a,EF=5a,DF==a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=5a,CD=DE+CE=7a,AB=7a,∠EBC=∠EBF,
又∵△ABF∽△DFE,∴===,
∴tan∠EBF==,tan∠EBC=tan∠EBF=;
(3)当△ABF∽△FBE时,∠2=∠4.
∵∠4=∠5,∠2+∠4+∠5=90°,∴∠2=∠4=∠5=30°,∴=cos30°=,
∵BC=BF,∴=k=;
②当△ABF∽△FEB时,∠2=∠6,∵∠4+∠6=90°,∴∠2+∠4=90°,
这与∠2+∠4+∠5=90°相矛盾,∴△ABF∽△FEB不成立.
综上所述,k=时,△ABF与△BFE相似.
【点评】本题考查的是矩形的性质、相似三角形的判定和性质以及锐角三角函数的概念,掌握有两个角相等的两个三角形相似是解题的关键,注意分情况讨论思想的灵活运用.
13. 解:(1)根据正对定义,当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,则sad60°==1.故答案为:1.
(2)当∠A接近0°时,sadA接近0,当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.于是sadA的取值范围是0<sadA<2.故答案为:0<sadA<2.
(3)在AB上取点D,使AD=AC,过点D作DE⊥AC于E,连接CD,如图.
∵在Rt△ADE中,=sin A=,设AD=AC=5x,则DE=3x,AE=4x.
∴CE=x.∴在Rt△CDE中,CD==x.
∴sad A===.
【点评】此题是一道新定义的题目,考查了等边三角形的判定与性质,直角三角形的性质,勾股定理等,要熟悉三角函数的定义,可进行类比解答.
1
1.∠α的补角是120°,则∠α=______,sinα=______.
2.已知△中,,3cosB=2,AC=,则AB= .
3.如图,△ABC的顶点都在方格纸的格点上,则sinA=_______.
(第3题) (第5题) (第6题)
4.菱形的两条对角线长分别是8和6,较短的一条对角线与菱形的一边的夹角为,则
sin=________,cos=________,tan=__________。
5.如图,将边长为的等边折叠,折痕为,点与点重合,和分别交于点、,,垂足为,.设的面积为,则重叠部分的面积为 .(用含的式子表示)
6.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=.则下列关系式中不成立的是( )
(A)tanA·cotA=1 (B)sinA=tanA·cosA (C)cosA=cotA·sinA (D)tan2A+cot2A=1
7.已知为锐角且=则等于( )
A. B. C. D.
8.在△ABC中,∠A=120°,AB=4,AC=2,则的值是
9.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1交AC于点D,如果AD=,则△ABC的周长等于 .
10. 先化简再求值:,其中.
11.
12.如图,点E是矩形ABCD中CD边上一点,⊿BCE沿BE折叠为⊿BFE,点F落在AD上.
(1)求证:⊿ABF∽⊿DFE;(2)若sin∠DFE=,求tan∠EBC的值.
13.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
(1)sad60°= 。
(2)对于0°
参考答案:
1.600,;2.6;3.;4.;5.;6.D;7.B;8.;9.;
10.;11.;
12. 解:(1)∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE,
(2)在Rt△DEF中,sin∠DFE==,
∴设DE=a,EF=3a,DF==2a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
∵△ABF∽△DFE,∴=,∴tan∠EBF==,
tan∠EBC=tan∠EBF=.
变式:如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE.
(2)若sin∠DFE=,求tan∠EBC的值.
(3)设=k,是否存在k的值,使△ABF与△BFE相似?若存在谋求出k的值;若不存在,请说明理由.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∵∠AFB+∠ABF=90°,∴∠ABF=∠DFE,∴△ABF∽△DFE;
(2)解:在Rt△DEF中,sin∠DFE==,
∴设DE=2a,EF=5a,DF==a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=5a,CD=DE+CE=7a,AB=7a,∠EBC=∠EBF,
又∵△ABF∽△DFE,∴===,
∴tan∠EBF==,tan∠EBC=tan∠EBF=;
(3)当△ABF∽△FBE时,∠2=∠4.
∵∠4=∠5,∠2+∠4+∠5=90°,∴∠2=∠4=∠5=30°,∴=cos30°=,
∵BC=BF,∴=k=;
②当△ABF∽△FEB时,∠2=∠6,∵∠4+∠6=90°,∴∠2+∠4=90°,
这与∠2+∠4+∠5=90°相矛盾,∴△ABF∽△FEB不成立.
综上所述,k=时,△ABF与△BFE相似.
【点评】本题考查的是矩形的性质、相似三角形的判定和性质以及锐角三角函数的概念,掌握有两个角相等的两个三角形相似是解题的关键,注意分情况讨论思想的灵活运用.
13. 解:(1)根据正对定义,当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,则sad60°==1.故答案为:1.
(2)当∠A接近0°时,sadA接近0,当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.于是sadA的取值范围是0<sadA<2.故答案为:0<sadA<2.
(3)在AB上取点D,使AD=AC,过点D作DE⊥AC于E,连接CD,如图.
∵在Rt△ADE中,=sin A=,设AD=AC=5x,则DE=3x,AE=4x.
∴CE=x.∴在Rt△CDE中,CD==x.
∴sad A===.
【点评】此题是一道新定义的题目,考查了等边三角形的判定与性质,直角三角形的性质,勾股定理等,要熟悉三角函数的定义,可进行类比解答.
1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
