苏科版八年级数学上 第3章 勾股定理测试题(word版,含答案)
文档属性
| 名称 | 苏科版八年级数学上 第3章 勾股定理测试题(word版,含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览

文档简介
第3章 勾股定理测试题
(本试卷满分100分 )
一、选择题(每小题3分,共30分)
1. 若一个直角三角形的两条直角边的长分别为6 cm和8 cm,则斜边的长为( )
A. 6 cm B. 8 cm C. 10 cm D. 14 cm
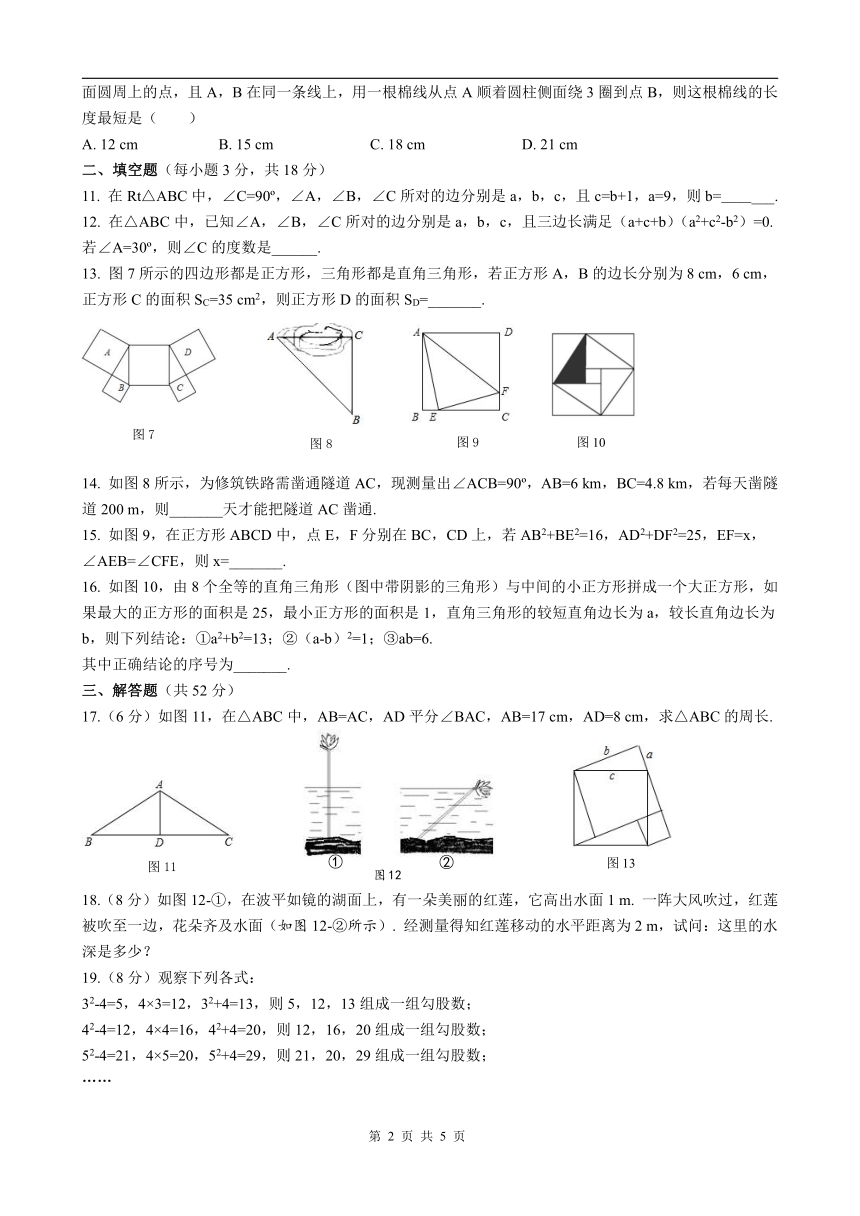
2. 如图1,在Rt△ABC中,∠ACB=90?,AB=13,BC=12.若以AC为边长作正方形(图中阴影部分),则这个正方形的面积为( )
A. 5 B. 10 C. 20 D. 25
3. 若三角形的三边长分别为3 cm,4 cm和5 cm,则这个三角形的最大内角的度数是( )
A. 45? B. 90? C. 135? D. 150?
4. 从5,9,12,13,17这5个数中选取3个数,可以作为勾股数的一组是( )
A. 5,9,12 B. 5,9,13 C. 5,12,13 D. 9,12,17
5.下面说法正确的是( )
A.在Rt△ABC中,∠A,∠B,∠C 所对的边分别为a,b,c,则a2+b2=c2
B.在Rt△ABC中,∠A,∠B,∠C 所对的边分别为a,b,c,若a=3,b=4,则c=5
C.直角三角形的两直角边长都是5,那么斜边长为10
D.直角三角形中,斜边最长
6. 图2的虚线部分是“赵爽弦图”示意图,它是由4个全等的直角三角形围成的,AC=3 cm,BC=2.5 cm,现将4个直角三角形中边长为3 cm的直角边分别向外延长1倍,得到如图所示的“数学风车”,则这个“数学风车”的外围周长是( )
A. 26 cm B. 34 cm C. 36 cm D. 38 cm
7. 如图3,在Rt△ABC中,∠C=90?,点D在BC上,连接AD,且AD=BD,若BD=10,BC=16,则AC的长为( )
A. 8 B. 10 C. 12 D. 14
图4所示是一个十字路口,O是两条公路的交点,点A,B,C,D分别表示公路上的四辆车.若OC=
80 m,AC=170 m,AB=50 m,BD2=50 000 m2,则C,D两辆车之间的距离为( )
A. 50 m B. 40 m C. 30 m D. 20 m
9. 如图5,在单位长度为1的正方形组成的网格图中标有AB,CD,AE,DE四条线段,其中能构成一个直角三角形的三条线段的是( )
A. AB,CD,AE B. AE,DE,CD
C. AE,DE,AB D. AB,CD,ED
10. 如图6,圆柱底面的半径为cm,高为9 cm,A,B分别是圆柱两底面圆周上的点,且A,B在同一条线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,则这根棉线的长度最短是( )
A. 12 cm B. 15 cm C. 18 cm D. 21 cm
二、填空题(每小题3分,共18分)
11. 在Rt△ABC中,∠C=90?,∠A,∠B,∠C所对的边分别是a,b,c,且c=b+1,a=9,则b=_____.
12. 在△ABC中,已知∠A,∠B,∠C所对的边分别是a,b,c,且三边长满足(a+c+b)(a2+c2-b2)=0.若∠A=30?,则∠C的度数是______.
13. 图7所示的四边形都是正方形,三角形都是直角三角形,若正方形A,B的边长分别为8 cm,6 cm,正方形C的面积SC=35 cm2,则正方形D的面积SD=_______.
14. 如图8所示,为修筑铁路需凿通隧道AC,现测量出∠ACB=90?,AB=6 km,BC=4.8 km,若每天凿隧道200 m,则_______天才能把隧道AC凿通.
15. 如图9,在正方形ABCD中,点E,F分别在BC,CD上,若AB2+BE2=16,AD2+DF2=25,EF=x,∠AEB=∠CFE,则x=_______.
16. 如图10,由8个全等的直角三角形(图中带阴影的三角形)与中间的小正方形拼成一个大正方形,如果最大的正方形的面积是25,最小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,则下列结论:①a2+b2=13;②(a-b)2=1;③ab=6.
其中正确结论的序号为_______.
三、解答题(共52分)
17.(6分)如图11,在△ABC中,AB=AC,AD平分∠BAC,AB=17 cm,AD=8 cm,求△ABC的周长.
18.(8分)如图12-①,在波平如镜的湖面上,有一朵美丽的红莲,它高出水面1 m. 一阵大风吹过,红莲被吹至一边,花朵齐及水面(如图12-②所示). 经测量得知红莲移动的水平距离为2 m,试问:这里的水深是多少?
19.(8分)观察下列各式:
32-4=5,4×3=12,32+4=13,则5,12,13组成一组勾股数;
42-4=12,4×4=16,42+4=20,则12,16,20组成一组勾股数;
52-4=21,4×5=20,52+4=29,则21,20,29组成一组勾股数;
……
你能否得出结论,对于任意大于2的整数k,k2-4,4k,k2+4组成一组勾股数?请说明理由.
20.(8分)图13所示是4个完全相同的直角三角形适当拼接后形成的图形,这些直角三角形的两条直角边长分别为a,b,斜边长为c.
(1)请你从面积的关系出发,写出一个关于a,b,c的等式,并验证你的结论正确;
(2)利用(1)中得到的等式解决问题:若a+b=7,ab=12,求c的值.
21. (10分)图14所示是一个长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm. 一只小虫想从鱼缸外的A点沿缸壁爬进鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线使爬行的路程最短?请你在图中画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路线长.
22. (12分)问题情境:在图15所示的正方形网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.
尝试解决:(1)在图15-①中画一个Rt△ABC,使其两直角边长分别为AB=3,BC=4(∠B=90?),并求出△ABC的周长;
(2)合作交流:在图15-②中,能否画出一个△EFG,使得EF2=20,FG2=5,EG=5,若能,求出∠EFG的度数;若不能,请说明理由.
第3章 勾股定理测试题参考答案
一、1. C 2. D 3. B 4. C 5. D 6. D 7. A 8. D 9. D
10. B 提示:圆柱体的展开图如图1所示,用一根棉线从A点顺着圆柱侧面绕3圈到B点的长度最短路线是AC→CD→DB.根据圆的周长公式可知,圆柱体的底面周长为
4 cm,即长方形的宽为4 cm,因为圆柱的高为9 cm,所以,每个小长方形的一条边长为3 cm,根据勾股定理,得AC=CD=DB=5 cm,所以AC+CD+DB=15(cm).
二、11. 40 12. 60? 13. 65 cm2 14. 18 15. 3
16. ①②③ 提示:因为最大正方形的面积为25,所以由四个全等直角三角形拼成的正方形的面积为13,所以a2+b2=13,①正确;因为最小正方形的面积为1,最小正方形的边长为b-a,所以(a-b)2=1,②正确;因为a2+b2-4×=(a-b)2,所以13-2ab=1,解得ab=6,③正确.
三、17. 解:因为AB=AC,AD平分∠BAC,所以AD⊥BC,BD=CD.根据勾股定理,得BD2=AB2-AD2=172-82=225,所以BD=15 cm,BC=2BD=30 cm.所以△ABC的周长为AB+AC+BC=17+17+30=64(cm).
18. 解:设水深为x m,则红莲的高为(x+1)m.
根据勾股定理,得x2+22=(x+1)2,解得x=1.5.故这里的水深为1.5 m.
解:能.理由:因为(k2-4)2+(4k)2=k4-8k2+16+16k2=k4+8k2+16,(k2+4)2=k4+8k2+16,所以
(k2-4)2+(4k)2=(k2+4)2.所以,对于任意大于2的整数k,k2-4,4k,k2+4组成一组勾股数.
20. 解:(1)该图形的面积有两种求法:一种是以c为边长的正方形的面积+2个直角三角形的面积;另一种是以b为边长的正方形的面积+以a为边长的正方形的面积+2个直角三角形的面积.根据两种求法的面积相等,得c2+2×ab=b2+2×ab+a2,化简,得a2+b2=c2.
(2)因为a+b=7,所以(a+b)2=49.所以a2+2ab+b2=49.
因为a2+b2=c2,ab=12,所以c2+2×12=49.所以c2=25,即c=5.
21. 解:(1)如图2所示,以BC所在直线为对称轴,作点A的对称点A′,连接A′G,则A′G的距离即为所求(即AQ+QG的长度).
(2)因为AE=40 cm,AA′=120 cm,所以A′E=120-40=80(cm). 在Rt△A′EG中,EG=60 cm,根据勾股定理,得A′G2=A′E2+EG2=802+602=10 000.所以A′G=100 cm.所以AQ+QG=A′Q+QG=A′G=100 cm.所以小虫爬行的最短路线长为100 cm.
22. 解:(1)如图3-①所示,在Rt△ABC中,AB=3,BC=4,根据勾股定理,得AC=5.
所以△ABC的周长=3+4+5=12.
(2)能.如图3-②所示,因为EF2+FG2=20+5=25,EG2=52=25,所以EF2+FG2=EG2.
所以△EFG是直角三角形,且∠EFG=90?.
第 1 页 共 4 页
(本试卷满分100分 )
一、选择题(每小题3分,共30分)
1. 若一个直角三角形的两条直角边的长分别为6 cm和8 cm,则斜边的长为( )
A. 6 cm B. 8 cm C. 10 cm D. 14 cm
2. 如图1,在Rt△ABC中,∠ACB=90?,AB=13,BC=12.若以AC为边长作正方形(图中阴影部分),则这个正方形的面积为( )
A. 5 B. 10 C. 20 D. 25
3. 若三角形的三边长分别为3 cm,4 cm和5 cm,则这个三角形的最大内角的度数是( )
A. 45? B. 90? C. 135? D. 150?
4. 从5,9,12,13,17这5个数中选取3个数,可以作为勾股数的一组是( )
A. 5,9,12 B. 5,9,13 C. 5,12,13 D. 9,12,17
5.下面说法正确的是( )
A.在Rt△ABC中,∠A,∠B,∠C 所对的边分别为a,b,c,则a2+b2=c2
B.在Rt△ABC中,∠A,∠B,∠C 所对的边分别为a,b,c,若a=3,b=4,则c=5
C.直角三角形的两直角边长都是5,那么斜边长为10
D.直角三角形中,斜边最长
6. 图2的虚线部分是“赵爽弦图”示意图,它是由4个全等的直角三角形围成的,AC=3 cm,BC=2.5 cm,现将4个直角三角形中边长为3 cm的直角边分别向外延长1倍,得到如图所示的“数学风车”,则这个“数学风车”的外围周长是( )
A. 26 cm B. 34 cm C. 36 cm D. 38 cm
7. 如图3,在Rt△ABC中,∠C=90?,点D在BC上,连接AD,且AD=BD,若BD=10,BC=16,则AC的长为( )
A. 8 B. 10 C. 12 D. 14
图4所示是一个十字路口,O是两条公路的交点,点A,B,C,D分别表示公路上的四辆车.若OC=
80 m,AC=170 m,AB=50 m,BD2=50 000 m2,则C,D两辆车之间的距离为( )
A. 50 m B. 40 m C. 30 m D. 20 m
9. 如图5,在单位长度为1的正方形组成的网格图中标有AB,CD,AE,DE四条线段,其中能构成一个直角三角形的三条线段的是( )
A. AB,CD,AE B. AE,DE,CD
C. AE,DE,AB D. AB,CD,ED
10. 如图6,圆柱底面的半径为cm,高为9 cm,A,B分别是圆柱两底面圆周上的点,且A,B在同一条线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,则这根棉线的长度最短是( )
A. 12 cm B. 15 cm C. 18 cm D. 21 cm
二、填空题(每小题3分,共18分)
11. 在Rt△ABC中,∠C=90?,∠A,∠B,∠C所对的边分别是a,b,c,且c=b+1,a=9,则b=_____.
12. 在△ABC中,已知∠A,∠B,∠C所对的边分别是a,b,c,且三边长满足(a+c+b)(a2+c2-b2)=0.若∠A=30?,则∠C的度数是______.
13. 图7所示的四边形都是正方形,三角形都是直角三角形,若正方形A,B的边长分别为8 cm,6 cm,正方形C的面积SC=35 cm2,则正方形D的面积SD=_______.
14. 如图8所示,为修筑铁路需凿通隧道AC,现测量出∠ACB=90?,AB=6 km,BC=4.8 km,若每天凿隧道200 m,则_______天才能把隧道AC凿通.
15. 如图9,在正方形ABCD中,点E,F分别在BC,CD上,若AB2+BE2=16,AD2+DF2=25,EF=x,∠AEB=∠CFE,则x=_______.
16. 如图10,由8个全等的直角三角形(图中带阴影的三角形)与中间的小正方形拼成一个大正方形,如果最大的正方形的面积是25,最小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,则下列结论:①a2+b2=13;②(a-b)2=1;③ab=6.
其中正确结论的序号为_______.
三、解答题(共52分)
17.(6分)如图11,在△ABC中,AB=AC,AD平分∠BAC,AB=17 cm,AD=8 cm,求△ABC的周长.
18.(8分)如图12-①,在波平如镜的湖面上,有一朵美丽的红莲,它高出水面1 m. 一阵大风吹过,红莲被吹至一边,花朵齐及水面(如图12-②所示). 经测量得知红莲移动的水平距离为2 m,试问:这里的水深是多少?
19.(8分)观察下列各式:
32-4=5,4×3=12,32+4=13,则5,12,13组成一组勾股数;
42-4=12,4×4=16,42+4=20,则12,16,20组成一组勾股数;
52-4=21,4×5=20,52+4=29,则21,20,29组成一组勾股数;
……
你能否得出结论,对于任意大于2的整数k,k2-4,4k,k2+4组成一组勾股数?请说明理由.
20.(8分)图13所示是4个完全相同的直角三角形适当拼接后形成的图形,这些直角三角形的两条直角边长分别为a,b,斜边长为c.
(1)请你从面积的关系出发,写出一个关于a,b,c的等式,并验证你的结论正确;
(2)利用(1)中得到的等式解决问题:若a+b=7,ab=12,求c的值.
21. (10分)图14所示是一个长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm. 一只小虫想从鱼缸外的A点沿缸壁爬进鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线使爬行的路程最短?请你在图中画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路线长.
22. (12分)问题情境:在图15所示的正方形网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.
尝试解决:(1)在图15-①中画一个Rt△ABC,使其两直角边长分别为AB=3,BC=4(∠B=90?),并求出△ABC的周长;
(2)合作交流:在图15-②中,能否画出一个△EFG,使得EF2=20,FG2=5,EG=5,若能,求出∠EFG的度数;若不能,请说明理由.
第3章 勾股定理测试题参考答案
一、1. C 2. D 3. B 4. C 5. D 6. D 7. A 8. D 9. D
10. B 提示:圆柱体的展开图如图1所示,用一根棉线从A点顺着圆柱侧面绕3圈到B点的长度最短路线是AC→CD→DB.根据圆的周长公式可知,圆柱体的底面周长为
4 cm,即长方形的宽为4 cm,因为圆柱的高为9 cm,所以,每个小长方形的一条边长为3 cm,根据勾股定理,得AC=CD=DB=5 cm,所以AC+CD+DB=15(cm).
二、11. 40 12. 60? 13. 65 cm2 14. 18 15. 3
16. ①②③ 提示:因为最大正方形的面积为25,所以由四个全等直角三角形拼成的正方形的面积为13,所以a2+b2=13,①正确;因为最小正方形的面积为1,最小正方形的边长为b-a,所以(a-b)2=1,②正确;因为a2+b2-4×=(a-b)2,所以13-2ab=1,解得ab=6,③正确.
三、17. 解:因为AB=AC,AD平分∠BAC,所以AD⊥BC,BD=CD.根据勾股定理,得BD2=AB2-AD2=172-82=225,所以BD=15 cm,BC=2BD=30 cm.所以△ABC的周长为AB+AC+BC=17+17+30=64(cm).
18. 解:设水深为x m,则红莲的高为(x+1)m.
根据勾股定理,得x2+22=(x+1)2,解得x=1.5.故这里的水深为1.5 m.
解:能.理由:因为(k2-4)2+(4k)2=k4-8k2+16+16k2=k4+8k2+16,(k2+4)2=k4+8k2+16,所以
(k2-4)2+(4k)2=(k2+4)2.所以,对于任意大于2的整数k,k2-4,4k,k2+4组成一组勾股数.
20. 解:(1)该图形的面积有两种求法:一种是以c为边长的正方形的面积+2个直角三角形的面积;另一种是以b为边长的正方形的面积+以a为边长的正方形的面积+2个直角三角形的面积.根据两种求法的面积相等,得c2+2×ab=b2+2×ab+a2,化简,得a2+b2=c2.
(2)因为a+b=7,所以(a+b)2=49.所以a2+2ab+b2=49.
因为a2+b2=c2,ab=12,所以c2+2×12=49.所以c2=25,即c=5.
21. 解:(1)如图2所示,以BC所在直线为对称轴,作点A的对称点A′,连接A′G,则A′G的距离即为所求(即AQ+QG的长度).
(2)因为AE=40 cm,AA′=120 cm,所以A′E=120-40=80(cm). 在Rt△A′EG中,EG=60 cm,根据勾股定理,得A′G2=A′E2+EG2=802+602=10 000.所以A′G=100 cm.所以AQ+QG=A′Q+QG=A′G=100 cm.所以小虫爬行的最短路线长为100 cm.
22. 解:(1)如图3-①所示,在Rt△ABC中,AB=3,BC=4,根据勾股定理,得AC=5.
所以△ABC的周长=3+4+5=12.
(2)能.如图3-②所示,因为EF2+FG2=20+5=25,EG2=52=25,所以EF2+FG2=EG2.
所以△EFG是直角三角形,且∠EFG=90?.
第 1 页 共 4 页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
