苏科版八年级数学上 第1章 全等三角形测试题(word版,含答案)
文档属性
| 名称 | 苏科版八年级数学上 第1章 全等三角形测试题(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览

文档简介
第1章 全等三角形测试题
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1. 下列可以判定两个直角三角形全等的条件是( )
A. 斜边相等 B. 面积相等 C. 两对锐角对应相等 D. 两对直角边对应相等
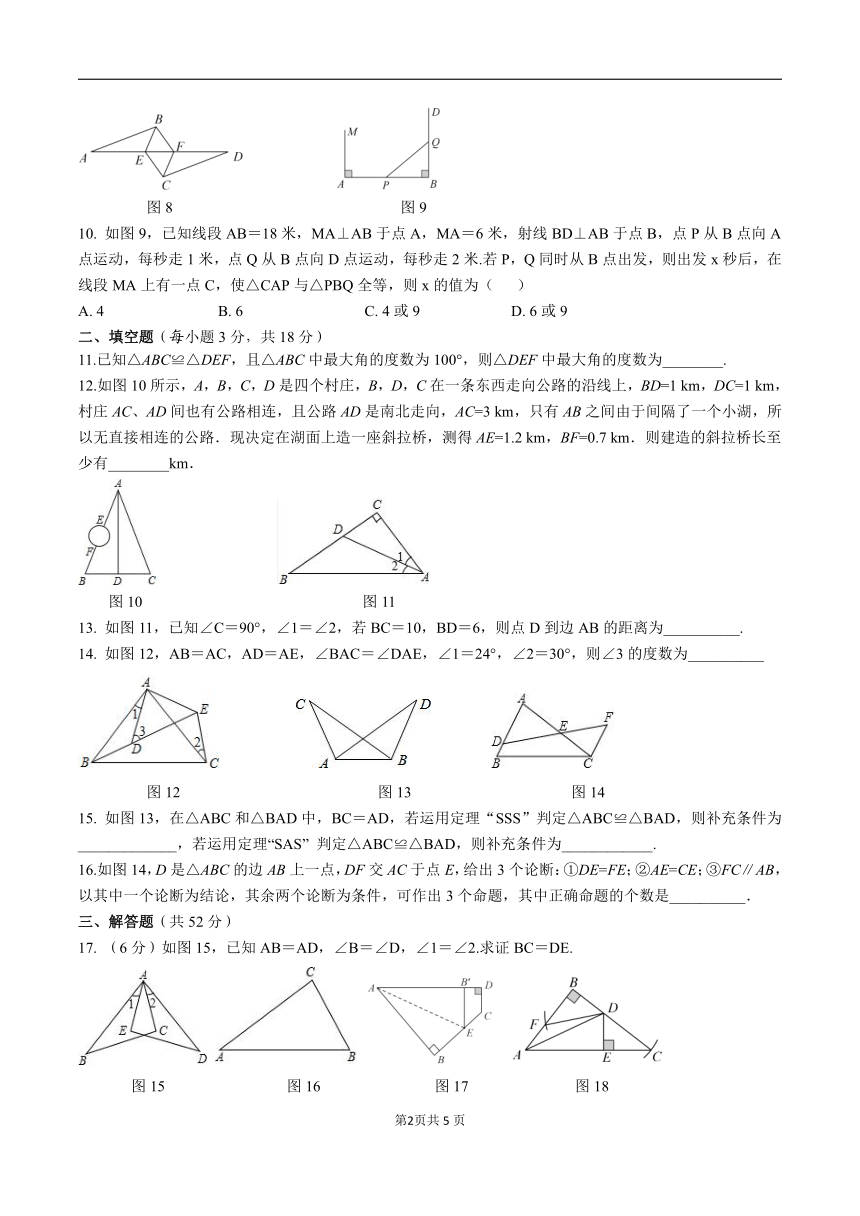
2. 如图1,将△ABC围绕点A旋转一定角度,使得∠DAC=25°,若∠B+∠C=110°,则∠EAC的度数为( )
A. 45° B. 40° C. 35° D. 25°
图1 图2 图3 图4
3. 如图2,AD⊥DC,AB⊥BC,若AB=AD,∠BCD=64°,则∠ACB的度数为( )
A. 21° B. 32° C. 36° D. 42°
4. 如图3,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A. 大于100 m B. 等于100 m C. 小于100 m D. 无法确定
5.如图4所示,BD、AC交于点O,若OA=OD,用“SAS”说明△AOB≌△DOC,还需条件( )
A.AB=DC B.OB=OC C.∠BAD=∠ADC D.∠AOB=∠DOC
6. 如图5,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,下列条件中,添加其中一个后仍无法证明△ABC≌△DEF,这个条件是( )
A. AC=DF B. BC=EF C. AC∥DF D. ∠A=∠D
图5 图6 图7
7. 图6所示是工人师傅用同一种材料制成的金属框架,已知AB=DE,AC=DF,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A. 45 cm B. 48 cm C. 51 cm D. 54 cm
8. 如图7,Rt△ABC中,∠ACB=90°,∠B=50°,D,F分别是BC,AC上的点,DE⊥AB,垂足为E,CF=BE,DF=DB,则∠ADE的度数为( )
A.40° B.50° C.70° D.71°
9. 如图8,AB∥CD,BE∥FC,AB=DC,则图中的全等三角形共有( )
A. 1对 B. 2对 C. 3对 D. 4对
图8 图9
10. 如图9,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于点B,点P从B点向A点运动,每秒走1米,点Q从B点向D点运动,每秒走2米.若P,Q同时从B点出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A. 4 B. 6 C. 4或9 D. 6或9
二、填空题(每小题3分,共18分)
11.已知△ABC≌△DEF,且△ABC中最大角的度数为100°,则△DEF中最大角的度数为________.
12.如图10所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄AC、AD间也有公路相连,且公路AD是南北走向,AC=3 km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2 km,BF=0.7 km.则建造的斜拉桥长至少有________km.
图10 图11
13. 如图11,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为__________.
14. 如图12,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,则∠3的度数为__________
图12 图13 图14
15. 如图13,在△ABC和△BAD中,BC=AD,若运用定理“SSS”判定△ABC≌△BAD,则补充条件为_____________,若运用定理“SAS” 判定△ABC≌△BAD,则补充条件为____________.
16.如图14,D是△ABC的边AB上一点,DF交AC于点E,给出3个论断:①DE=FE;②AE=CE;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出3个命题,其中正确命题的个数是__________.
三、解答题(共52分)
17. (6分)如图15,已知AB=AD,∠B=∠D,∠1=∠2.求证BC=DE.
图15 图16 图17 图18
18.(7分)如图16,在△ABC中,AC=6,BC=4.
(1)用直尺和圆规作∠ACB的平分线CD,交AB于点D;(保留作图痕迹,不要求写作法和证明)
(2)在(1)所作的图形中,若△ACD的面积为3,求△BCD的面积.
19.(8分)图17所示是一个四边形纸片ABCD,∠B=∠D=90°,将纸片按图中所示折叠,使点B落在AD边上的点B′处,AE是折痕.
(1)判断B′E与DC的位置关系,说明理由;
(2)如果∠C=130°,求∠AEB的度数.
20.(9分)如图18,在Rt△ABC中,∠B=90°,D是BC上一点,过点D作DE⊥AC于点E;再以点D为圆心,CD的长为半径画弧交AB于点F,使得BF=CE.
(1)求证:AD是∠BAC的平分线;
4829175635(2)若∠C=40°,求∠ADF的度数.
21.(10分)如图19,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度
509333512446022.(12分)如图20,在△ABC中,∠B=∠C,AB=AC=10 cm,BC=8 cm,D为AB的中点,点P在线段BC上以1 cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P相同,当运动时间为3 s时,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P不相同,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
附加题(20分,不计入总分)
23. 如图21,在△ABC中,M是BC边上一动点(不与点B,C重合),N是BC边的中点,CF⊥AM于点F,BE⊥AM于点E,BA⊥AC.
(1)如图21-①,当点N,M重合时,ME和MF的数量关系是_________,BE和CF的位置关系是____________;
(2)如图21-②,当点N不与点M重合时,延长FN交BE于点P,则△NFE的面积S1与△PFE的面积S2的关系为_________,请说明理由;
(3)若点M在CB的延长线上,延长EN交CF于点P,(2)中的结论是否仍然成立?请在备用图中画出图形,不需要证明.
① ② 备用图
图21
第1章 全等三角形测试题参考答案
一、1. D 2. A 3. B 4. B 5. B 6. A 7. A 8. C 9. C
10. B 提示:当△APC≌△BQP时,AP=BQ,即18-x=2x,解得x=6;当△APC≌△BPQ时,AP=BP=falseAB=9米,此时所用时间为9秒,AC=BQ=18米,而已知MA=6米,所以不合题意,舍去.
综上所述,出发6秒,在线段MA上有一点C,使△CAP与△PBQ全等.
二、11.100° 12. 1.1 13. 4 14. 54° 15. AC=BD ∠ABC=∠BAD 16. 150°
三、17. 证明:因为∠1=∠2,所以∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,∠BAC=∠DAE,AB=AD,∠B=∠D,所以△ABC≌△ADE(ASA).
所以BC=DE.
18. 解:(1)如图1所示,CD即为所求作的角平分线.
453517071755(2)过点D分别作DE⊥AC于点E,DF⊥BC于点F,如图1所示.
因为CD是∠ACB的平分线,所以DE=DF.
因为S△ACD=falseAC?DE=3,即false×6DE=3,解得DE=1,则DF=1.
所以S△BCD=falseBC?DF=false×4×1=2.
19. 解:(1)B′E∥DC. 图1
理由:由折叠的性质,知△ABE≌△AB′E,所以∠AB′E=∠B=∠D=90°.所以B′E∥DC.
(2)由折叠的性质,知∠AEB′=∠AEB,即∠AEB=false∠BEB′.
因为B′E∥DC,所以∠BEB′=∠C=130°.所以∠AEB=false∠BEB′=65°.
20.(1)证明:在Rt△BDF和Rt△EDC中,DF=DC,BF=EC,所以Rt△BDF≌Rt△EDC(HL).
所以DB=DE.
因为DB⊥AB,DE⊥AC,所以AD是∠BAC的平分线.
(2)解:因为Rt△BDF≌Rt△EDC,所以∠BFD=∠C=40°.
因为AD平分∠BAC,所以∠BAD=false(90°-∠C)=25°.
所以∠ADF=∠BFD-∠BAD=40°-25°=15°.
21. 证明:如图,延长CE交AB于F,则∠A+∠1=90°,∠C+∠2=90°.
∵∠1=∠2,
∴∠A=∠C.
在△ABD和△CDE中,∠A=∠C,AB=CD,∠ABD=∠CDE=90°,
∴△ABD≌△CDE(ASA).
∴DB=DE.
∵DE=2米,
∴DB的长度是2米.
(第21题解图)
22. 解:(1)当运动时间为3 s时,△BPD≌△CQP.
理由:由题意,知BP=CQ=3 cm.
因为D是AB的中点,所以BD=falseAB=5 cm,CP=8-3=5(cm).所以BD=CP.
又因为∠B=∠C,?所以△BPD≌△CQP(SAS).
(2)在△BPD和△CQP中,已知∠B=∠C.
设点Q的速度为x cm/s,时间为t s.
当BP=CP,CQ=BD=5 cm时,△BPD≌△CPQ,此时BP=falseBC=4 cm ,故t=4 s.
由题意,得4x=5,解得x=false;
由于点P,Q的速度不同,所以BP≠CQ.
所以点Q的运动速度为falsecm/s时,能够使得△BPD≌△CPQ.
489077016065523. 解:(1)相等 平行
提示:因为CF⊥AM,BE⊥AM,所以CF∥BE.所以∠MCF=∠MBE.
因为M是BC的中点,所以BM=CM.
因为∠FMC=∠EMB,所以△FMC≌△EMB(AAS).所以ME=MF.
(2)2S1=S2.
理由:如图3所示,因为CF⊥AM,BE⊥AM,所以CF∥BE.所以∠1=∠2.
因为N是BC的中点,所以BN=CN.
因为∠3=∠4,所以△PBN≌△FCN(ASA).所以NP=NF. 图3
4839970150495所以NE是Rt△FEP的中线.所以△PFE的面积是△NFE面积的2倍,即2S1=S2.
(3)(2)中的结论仍然成立,如图4所示.
证明:因为CF⊥AM,BE⊥AM,所以CF∥BE,∠CFE=90°.所以∠1=∠2.
因为N是BC的中点,所以BN=CN.
又因为∠4=∠3,所以△ENB≌△PNC(AAS).所以NE=NP.
所以NF是Rt△EFP的中线.所以△PFE的面积是△NFE面积的2倍,即2S1=S2.
图4
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1. 下列可以判定两个直角三角形全等的条件是( )
A. 斜边相等 B. 面积相等 C. 两对锐角对应相等 D. 两对直角边对应相等
2. 如图1,将△ABC围绕点A旋转一定角度,使得∠DAC=25°,若∠B+∠C=110°,则∠EAC的度数为( )
A. 45° B. 40° C. 35° D. 25°
图1 图2 图3 图4
3. 如图2,AD⊥DC,AB⊥BC,若AB=AD,∠BCD=64°,则∠ACB的度数为( )
A. 21° B. 32° C. 36° D. 42°
4. 如图3,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
A. 大于100 m B. 等于100 m C. 小于100 m D. 无法确定
5.如图4所示,BD、AC交于点O,若OA=OD,用“SAS”说明△AOB≌△DOC,还需条件( )
A.AB=DC B.OB=OC C.∠BAD=∠ADC D.∠AOB=∠DOC
6. 如图5,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,下列条件中,添加其中一个后仍无法证明△ABC≌△DEF,这个条件是( )
A. AC=DF B. BC=EF C. AC∥DF D. ∠A=∠D
图5 图6 图7
7. 图6所示是工人师傅用同一种材料制成的金属框架,已知AB=DE,AC=DF,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A. 45 cm B. 48 cm C. 51 cm D. 54 cm
8. 如图7,Rt△ABC中,∠ACB=90°,∠B=50°,D,F分别是BC,AC上的点,DE⊥AB,垂足为E,CF=BE,DF=DB,则∠ADE的度数为( )
A.40° B.50° C.70° D.71°
9. 如图8,AB∥CD,BE∥FC,AB=DC,则图中的全等三角形共有( )
A. 1对 B. 2对 C. 3对 D. 4对
图8 图9
10. 如图9,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于点B,点P从B点向A点运动,每秒走1米,点Q从B点向D点运动,每秒走2米.若P,Q同时从B点出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A. 4 B. 6 C. 4或9 D. 6或9
二、填空题(每小题3分,共18分)
11.已知△ABC≌△DEF,且△ABC中最大角的度数为100°,则△DEF中最大角的度数为________.
12.如图10所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄AC、AD间也有公路相连,且公路AD是南北走向,AC=3 km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2 km,BF=0.7 km.则建造的斜拉桥长至少有________km.
图10 图11
13. 如图11,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为__________.
14. 如图12,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=30°,则∠3的度数为__________
图12 图13 图14
15. 如图13,在△ABC和△BAD中,BC=AD,若运用定理“SSS”判定△ABC≌△BAD,则补充条件为_____________,若运用定理“SAS” 判定△ABC≌△BAD,则补充条件为____________.
16.如图14,D是△ABC的边AB上一点,DF交AC于点E,给出3个论断:①DE=FE;②AE=CE;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出3个命题,其中正确命题的个数是__________.
三、解答题(共52分)
17. (6分)如图15,已知AB=AD,∠B=∠D,∠1=∠2.求证BC=DE.
图15 图16 图17 图18
18.(7分)如图16,在△ABC中,AC=6,BC=4.
(1)用直尺和圆规作∠ACB的平分线CD,交AB于点D;(保留作图痕迹,不要求写作法和证明)
(2)在(1)所作的图形中,若△ACD的面积为3,求△BCD的面积.
19.(8分)图17所示是一个四边形纸片ABCD,∠B=∠D=90°,将纸片按图中所示折叠,使点B落在AD边上的点B′处,AE是折痕.
(1)判断B′E与DC的位置关系,说明理由;
(2)如果∠C=130°,求∠AEB的度数.
20.(9分)如图18,在Rt△ABC中,∠B=90°,D是BC上一点,过点D作DE⊥AC于点E;再以点D为圆心,CD的长为半径画弧交AB于点F,使得BF=CE.
(1)求证:AD是∠BAC的平分线;
4829175635(2)若∠C=40°,求∠ADF的度数.
21.(10分)如图19,AD是一段斜坡,AB是水平线,现为了测斜坡上一点D的铅直高度(即垂线段DB的长度),小亮在D处立上一竹竿CD,并保证CD=AB,CD⊥AD,然后在竿顶C处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直).细绳与斜坡AD交于点E,此时他测得DE=2米,求DB的长度
509333512446022.(12分)如图20,在△ABC中,∠B=∠C,AB=AC=10 cm,BC=8 cm,D为AB的中点,点P在线段BC上以1 cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P相同,当运动时间为3 s时,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P不相同,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
附加题(20分,不计入总分)
23. 如图21,在△ABC中,M是BC边上一动点(不与点B,C重合),N是BC边的中点,CF⊥AM于点F,BE⊥AM于点E,BA⊥AC.
(1)如图21-①,当点N,M重合时,ME和MF的数量关系是_________,BE和CF的位置关系是____________;
(2)如图21-②,当点N不与点M重合时,延长FN交BE于点P,则△NFE的面积S1与△PFE的面积S2的关系为_________,请说明理由;
(3)若点M在CB的延长线上,延长EN交CF于点P,(2)中的结论是否仍然成立?请在备用图中画出图形,不需要证明.
① ② 备用图
图21
第1章 全等三角形测试题参考答案
一、1. D 2. A 3. B 4. B 5. B 6. A 7. A 8. C 9. C
10. B 提示:当△APC≌△BQP时,AP=BQ,即18-x=2x,解得x=6;当△APC≌△BPQ时,AP=BP=falseAB=9米,此时所用时间为9秒,AC=BQ=18米,而已知MA=6米,所以不合题意,舍去.
综上所述,出发6秒,在线段MA上有一点C,使△CAP与△PBQ全等.
二、11.100° 12. 1.1 13. 4 14. 54° 15. AC=BD ∠ABC=∠BAD 16. 150°
三、17. 证明:因为∠1=∠2,所以∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,∠BAC=∠DAE,AB=AD,∠B=∠D,所以△ABC≌△ADE(ASA).
所以BC=DE.
18. 解:(1)如图1所示,CD即为所求作的角平分线.
453517071755(2)过点D分别作DE⊥AC于点E,DF⊥BC于点F,如图1所示.
因为CD是∠ACB的平分线,所以DE=DF.
因为S△ACD=falseAC?DE=3,即false×6DE=3,解得DE=1,则DF=1.
所以S△BCD=falseBC?DF=false×4×1=2.
19. 解:(1)B′E∥DC. 图1
理由:由折叠的性质,知△ABE≌△AB′E,所以∠AB′E=∠B=∠D=90°.所以B′E∥DC.
(2)由折叠的性质,知∠AEB′=∠AEB,即∠AEB=false∠BEB′.
因为B′E∥DC,所以∠BEB′=∠C=130°.所以∠AEB=false∠BEB′=65°.
20.(1)证明:在Rt△BDF和Rt△EDC中,DF=DC,BF=EC,所以Rt△BDF≌Rt△EDC(HL).
所以DB=DE.
因为DB⊥AB,DE⊥AC,所以AD是∠BAC的平分线.
(2)解:因为Rt△BDF≌Rt△EDC,所以∠BFD=∠C=40°.
因为AD平分∠BAC,所以∠BAD=false(90°-∠C)=25°.
所以∠ADF=∠BFD-∠BAD=40°-25°=15°.
21. 证明:如图,延长CE交AB于F,则∠A+∠1=90°,∠C+∠2=90°.
∵∠1=∠2,
∴∠A=∠C.
在△ABD和△CDE中,∠A=∠C,AB=CD,∠ABD=∠CDE=90°,
∴△ABD≌△CDE(ASA).
∴DB=DE.
∵DE=2米,
∴DB的长度是2米.
(第21题解图)
22. 解:(1)当运动时间为3 s时,△BPD≌△CQP.
理由:由题意,知BP=CQ=3 cm.
因为D是AB的中点,所以BD=falseAB=5 cm,CP=8-3=5(cm).所以BD=CP.
又因为∠B=∠C,?所以△BPD≌△CQP(SAS).
(2)在△BPD和△CQP中,已知∠B=∠C.
设点Q的速度为x cm/s,时间为t s.
当BP=CP,CQ=BD=5 cm时,△BPD≌△CPQ,此时BP=falseBC=4 cm ,故t=4 s.
由题意,得4x=5,解得x=false;
由于点P,Q的速度不同,所以BP≠CQ.
所以点Q的运动速度为falsecm/s时,能够使得△BPD≌△CPQ.
489077016065523. 解:(1)相等 平行
提示:因为CF⊥AM,BE⊥AM,所以CF∥BE.所以∠MCF=∠MBE.
因为M是BC的中点,所以BM=CM.
因为∠FMC=∠EMB,所以△FMC≌△EMB(AAS).所以ME=MF.
(2)2S1=S2.
理由:如图3所示,因为CF⊥AM,BE⊥AM,所以CF∥BE.所以∠1=∠2.
因为N是BC的中点,所以BN=CN.
因为∠3=∠4,所以△PBN≌△FCN(ASA).所以NP=NF. 图3
4839970150495所以NE是Rt△FEP的中线.所以△PFE的面积是△NFE面积的2倍,即2S1=S2.
(3)(2)中的结论仍然成立,如图4所示.
证明:因为CF⊥AM,BE⊥AM,所以CF∥BE,∠CFE=90°.所以∠1=∠2.
因为N是BC的中点,所以BN=CN.
又因为∠4=∠3,所以△ENB≌△PNC(AAS).所以NE=NP.
所以NF是Rt△EFP的中线.所以△PFE的面积是△NFE面积的2倍,即2S1=S2.
图4
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
