苏科版八年级数学上 第5章 平面直角坐标系测试题(word版,含答案)
文档属性
| 名称 | 苏科版八年级数学上 第5章 平面直角坐标系测试题(word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 264.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览


文档简介
第5章 平面直角坐标系测试题
(本试卷满分100分 )
一、选择题(每小题3分,共30分)
1.上海合作组织青岛峰会将于2018年6月在山东青岛举行,下列能准确表示青岛地理位置的是( )
A.山东半岛东南部 B.东经约120°
C.北纬约36° D.东经约120°,北纬约36°
2.下列各点,不能与点(2,-1)通过上、下平移重合的点是( )
A.(2,-2) B.(-2,-1) C.(2,0) D.(2,-3)
3.如图1,AB∥CD,AD∥BC∥x轴,则下列说法正确的是( )
A.A与D的横坐标相同 B.A与B的横坐标相同
C.B与C的纵坐标相同 D.C与D的纵坐标相同
图1 图2 图3 图4
4.如图2,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(4,﹣6),则点A的坐标为( )
A.(﹣6,6) B.(﹣4,6) C.(6,4) D.(﹣4,4)
5.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5) C.(-8,-1) D.(2,-1)
6.共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图3,“”为小白同学的位置,“★”为检索到的共享单车停放点,为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A.F6 B.E6 C.D5 D.F7
7.在平面直角坐标系中有一点M(a,b),并且ab=0,则点M的位置在( )
A. 原点上 B. x轴上 C. y轴上 D. 坐标轴上
8. A,B,C三点在坐标平面上的位置如图4所示,若A,B,C的横坐标的总和为a,纵坐标的总和为b,则a-b的值为( )
A. 5 B. 3 C. -3 D. -5
9.在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出下列定义:若b′=,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5),如果一个点的限变点的坐标是(,-1),那么这个点的坐标是( )
A.(-1,) B.(-,-1) C.(,-1) D.(,1)
10.如图5,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,第n秒时点P的位置记为Pn,则第2017秒时,即点P2018的坐标是( )
A.(2017,0) B.(2018,1) C.(2018,-1) D.(2018,0)
图5
二、填空题(每小题3分,共18分)
11.写出一个平面直角坐标系中第三象限内点的坐标: .
12. 若点A(﹣2,1)与B(a,b)关于y轴对称,则a+b= .
13.如图6,这是怀柔区部分景点的分布图,若表示百泉山风景区的点的坐标为(0,1),表示慕田峪长城的点的坐标为(﹣5,﹣1),则表示雁栖湖的点的坐标为 .
图6 图7
14.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B点的坐标为_______.
15.已知点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为4,则点P的坐标是
.
16. 如图7,在平面直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a,b均为正整数,则符合题意的点C的坐标有_______个.
三、解答题(共52分)
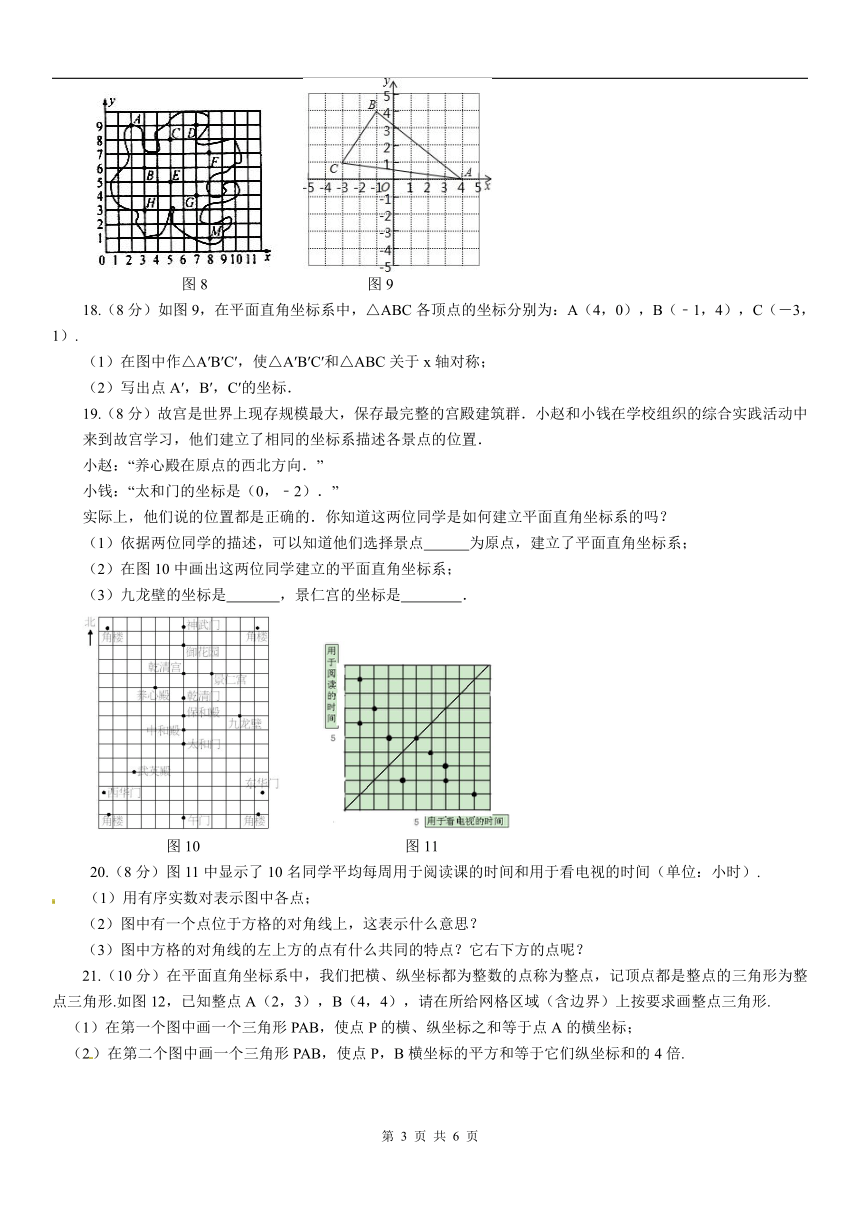
17.(6分)图8是画在平面直角坐标系中的某一小岛的示意图.
(1)分别写出点A,C,E,G,M的坐标;
(2)(3,6),(7,9),(8,7),(3,3)所代表的地点分别是什么?
图8 图9
18.(8分)如图9,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(-3,1).
(1)在图中作△A′B′C′,使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′,B′,C′的坐标.
19.(8分)故宫是世界上现存规模最大,保存最完整的宫殿建筑群.小赵和小钱在学校组织的综合实践活动中来到故宫学习,他们建立了相同的坐标系描述各景点的位置.
小赵:“养心殿在原点的西北方向.”
小钱:“太和门的坐标是(0,﹣2).”
实际上,他们说的位置都是正确的.你知道这两位同学是如何建立平面直角坐标系的吗?
(1)依据两位同学的描述,可以知道他们选择景点 为原点,建立了平面直角坐标系;
(2)在图10中画出这两位同学建立的平面直角坐标系;
(3)九龙壁的坐标是 ,景仁宫的坐标是 .
图10 图11
20.(8分)图11中显示了10名同学平均每周用于阅读课的时间和用于看电视的时间(单位:小时).
(1)用有序实数对表示图中各点;
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格的对角线的左上方的点有什么共同的特点?它右下方的点呢?
21.(10分)在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图12,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在第一个图中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在第二个图中画一个三角形PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
图12
22. (12分)在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在图13所示的坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
图13
附加题(20分,不计入总分)
23.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题:
(1)若已知点D(1,2),E(﹣2,1),F(0,6),则这三点的“矩面积”为 .
(2)若D(1,2),E(﹣2,1),F(0,t)三点的“矩面积”为18,求点F的坐标.
第5章 平面直角坐标系测试题参考答案
一、1.D 2.B 3.C 4.B 5.D 6.A 7.D 8.A 9.C
10. D 提示:由已知,得P0(0,0),P1(1,1),P2(2,0),P3(3,-1),P4(4,0),P5(5,1),…,所以P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1),其中n是整数,且n≥0.因为2018=504×4+2,所以点P2018的坐标为(2018,0).
二、11.答案不唯一,如(-1,-1) 12.3 13. (1,﹣3) 14. (8,2)或(-2,2)
15. (,) 16. 5
三、17. 解:(1)点A,C,E,G,M的坐标分别为A(2,9),C(5,8),E(5,5),G(7,4),M(8,1).
(3,6),(7,9),(8,7),(3,3)分别代表点B,D,F,H.
18.(1)图略.(2) A′(4,0),B′(-1,-4),C′(-3,-1).
19. 解:(1)保和殿 (2)图略. (3)(4,0) (2,3)
20. 解:(1)答案不唯一,如分别可表示为:(1,9),(1,6),(2,7),(3,5),(4,2),(5,5),(6,4),(7,3),(7,2),(9,1).
(2)位于方格的对角线上的点表示该同学每周看电视和阅读的时间是一样的.
(3)答案不唯一,如左上方的点的共同特征是每周阅读的时间都不少于5小时,且看电视的时间不超过3小时;右下方的点共同特征是看电视的时间都不少于4小时,阅读的时间都不超过4小时.
21. 解:(1)设P(x,y),由题意,得x+y=2.
因为x,y均为整数,在所给区域内点P的坐标为(2,0),(1,1)或(0,2).当点P的坐标为(0,2)时,点P,A,B构不成三角形,所以点P的坐标为(2,0)或(1,1),画出△PAB略.
(2)设P(x,y),由题意,得x2+42=4(4+y),整理得x2=4y.因为x,y为整数,所以在所给区域内点P的坐标为(2,1),(0,0)或(4,4).当点P的坐标为(4,4)时,点P,B重合,所以点P的坐标为(2,1)或(0,0),画出△PAB略.
22. 解:(1)如图所示:
(2)如图,过点C向x轴,y轴作垂线,垂足分别为D,E.S四边形DOEC=3×4=12,S△BCD=×2×3=3,
S△ACE=×2×4=4,S△AOB=×2×1=1.所以S△ABC=S四边形DOEC-S△BCD-S△ACE-S△AOB=12-3-4-1=4.
(3)当点P在x轴上时,S△ABP=AO×BP=4,即×1×BP=4,解得BP=8,所以点P的坐标为(10,0)或(-6,0).当点P在y轴上时,S△ABP=BO×AP=4,即×2×AP=4,解得AP=4,所以点P的坐标为(0,5)或(0,-3).综上,点P的坐标为(0,5),(0,-3),(10,0)或(-6,0).
23. 解:(1)15 提示:由题意得a=1﹣(﹣2)=3,h=6﹣1=5,所以S=ah=3×5=15.
(2)由题意得 “水平底”a=1﹣(﹣2)=3.
当t>2时,h=t﹣1,则3(t﹣1)=18,解得t=7.
故点F的坐标为(0,7);
当1≤t≤2时,h=2﹣1=1≠6,故此种情况不符合题意;
当t<1时,h=2﹣t,则3(2﹣t)=18,解得t=﹣4.
故点F的坐标为(0,﹣4).
所以,点F的坐标为(0,7)或(0,﹣4).
第 1 页 共 6 页
(本试卷满分100分 )
一、选择题(每小题3分,共30分)
1.上海合作组织青岛峰会将于2018年6月在山东青岛举行,下列能准确表示青岛地理位置的是( )
A.山东半岛东南部 B.东经约120°
C.北纬约36° D.东经约120°,北纬约36°
2.下列各点,不能与点(2,-1)通过上、下平移重合的点是( )
A.(2,-2) B.(-2,-1) C.(2,0) D.(2,-3)
3.如图1,AB∥CD,AD∥BC∥x轴,则下列说法正确的是( )
A.A与D的横坐标相同 B.A与B的横坐标相同
C.B与C的纵坐标相同 D.C与D的纵坐标相同
图1 图2 图3 图4
4.如图2,△OAB和△OCB关于x轴对称,△OCD和△OED关于y轴对称,若点E的坐标为(4,﹣6),则点A的坐标为( )
A.(﹣6,6) B.(﹣4,6) C.(6,4) D.(﹣4,4)
5.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5) C.(-8,-1) D.(2,-1)
6.共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图3,“”为小白同学的位置,“★”为检索到的共享单车停放点,为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A.F6 B.E6 C.D5 D.F7
7.在平面直角坐标系中有一点M(a,b),并且ab=0,则点M的位置在( )
A. 原点上 B. x轴上 C. y轴上 D. 坐标轴上
8. A,B,C三点在坐标平面上的位置如图4所示,若A,B,C的横坐标的总和为a,纵坐标的总和为b,则a-b的值为( )
A. 5 B. 3 C. -3 D. -5
9.在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出下列定义:若b′=,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5),如果一个点的限变点的坐标是(,-1),那么这个点的坐标是( )
A.(-1,) B.(-,-1) C.(,-1) D.(,1)
10.如图5,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,第n秒时点P的位置记为Pn,则第2017秒时,即点P2018的坐标是( )
A.(2017,0) B.(2018,1) C.(2018,-1) D.(2018,0)
图5
二、填空题(每小题3分,共18分)
11.写出一个平面直角坐标系中第三象限内点的坐标: .
12. 若点A(﹣2,1)与B(a,b)关于y轴对称,则a+b= .
13.如图6,这是怀柔区部分景点的分布图,若表示百泉山风景区的点的坐标为(0,1),表示慕田峪长城的点的坐标为(﹣5,﹣1),则表示雁栖湖的点的坐标为 .
图6 图7
14.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B点的坐标为_______.
15.已知点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为4,则点P的坐标是
.
16. 如图7,在平面直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a,b均为正整数,则符合题意的点C的坐标有_______个.
三、解答题(共52分)
17.(6分)图8是画在平面直角坐标系中的某一小岛的示意图.
(1)分别写出点A,C,E,G,M的坐标;
(2)(3,6),(7,9),(8,7),(3,3)所代表的地点分别是什么?
图8 图9
18.(8分)如图9,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(-3,1).
(1)在图中作△A′B′C′,使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′,B′,C′的坐标.
19.(8分)故宫是世界上现存规模最大,保存最完整的宫殿建筑群.小赵和小钱在学校组织的综合实践活动中来到故宫学习,他们建立了相同的坐标系描述各景点的位置.
小赵:“养心殿在原点的西北方向.”
小钱:“太和门的坐标是(0,﹣2).”
实际上,他们说的位置都是正确的.你知道这两位同学是如何建立平面直角坐标系的吗?
(1)依据两位同学的描述,可以知道他们选择景点 为原点,建立了平面直角坐标系;
(2)在图10中画出这两位同学建立的平面直角坐标系;
(3)九龙壁的坐标是 ,景仁宫的坐标是 .
图10 图11
20.(8分)图11中显示了10名同学平均每周用于阅读课的时间和用于看电视的时间(单位:小时).
(1)用有序实数对表示图中各点;
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格的对角线的左上方的点有什么共同的特点?它右下方的点呢?
21.(10分)在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图12,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在第一个图中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在第二个图中画一个三角形PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
图12
22. (12分)在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在图13所示的坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
图13
附加题(20分,不计入总分)
23.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题:
(1)若已知点D(1,2),E(﹣2,1),F(0,6),则这三点的“矩面积”为 .
(2)若D(1,2),E(﹣2,1),F(0,t)三点的“矩面积”为18,求点F的坐标.
第5章 平面直角坐标系测试题参考答案
一、1.D 2.B 3.C 4.B 5.D 6.A 7.D 8.A 9.C
10. D 提示:由已知,得P0(0,0),P1(1,1),P2(2,0),P3(3,-1),P4(4,0),P5(5,1),…,所以P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1),其中n是整数,且n≥0.因为2018=504×4+2,所以点P2018的坐标为(2018,0).
二、11.答案不唯一,如(-1,-1) 12.3 13. (1,﹣3) 14. (8,2)或(-2,2)
15. (,) 16. 5
三、17. 解:(1)点A,C,E,G,M的坐标分别为A(2,9),C(5,8),E(5,5),G(7,4),M(8,1).
(3,6),(7,9),(8,7),(3,3)分别代表点B,D,F,H.
18.(1)图略.(2) A′(4,0),B′(-1,-4),C′(-3,-1).
19. 解:(1)保和殿 (2)图略. (3)(4,0) (2,3)
20. 解:(1)答案不唯一,如分别可表示为:(1,9),(1,6),(2,7),(3,5),(4,2),(5,5),(6,4),(7,3),(7,2),(9,1).
(2)位于方格的对角线上的点表示该同学每周看电视和阅读的时间是一样的.
(3)答案不唯一,如左上方的点的共同特征是每周阅读的时间都不少于5小时,且看电视的时间不超过3小时;右下方的点共同特征是看电视的时间都不少于4小时,阅读的时间都不超过4小时.
21. 解:(1)设P(x,y),由题意,得x+y=2.
因为x,y均为整数,在所给区域内点P的坐标为(2,0),(1,1)或(0,2).当点P的坐标为(0,2)时,点P,A,B构不成三角形,所以点P的坐标为(2,0)或(1,1),画出△PAB略.
(2)设P(x,y),由题意,得x2+42=4(4+y),整理得x2=4y.因为x,y为整数,所以在所给区域内点P的坐标为(2,1),(0,0)或(4,4).当点P的坐标为(4,4)时,点P,B重合,所以点P的坐标为(2,1)或(0,0),画出△PAB略.
22. 解:(1)如图所示:
(2)如图,过点C向x轴,y轴作垂线,垂足分别为D,E.S四边形DOEC=3×4=12,S△BCD=×2×3=3,
S△ACE=×2×4=4,S△AOB=×2×1=1.所以S△ABC=S四边形DOEC-S△BCD-S△ACE-S△AOB=12-3-4-1=4.
(3)当点P在x轴上时,S△ABP=AO×BP=4,即×1×BP=4,解得BP=8,所以点P的坐标为(10,0)或(-6,0).当点P在y轴上时,S△ABP=BO×AP=4,即×2×AP=4,解得AP=4,所以点P的坐标为(0,5)或(0,-3).综上,点P的坐标为(0,5),(0,-3),(10,0)或(-6,0).
23. 解:(1)15 提示:由题意得a=1﹣(﹣2)=3,h=6﹣1=5,所以S=ah=3×5=15.
(2)由题意得 “水平底”a=1﹣(﹣2)=3.
当t>2时,h=t﹣1,则3(t﹣1)=18,解得t=7.
故点F的坐标为(0,7);
当1≤t≤2时,h=2﹣1=1≠6,故此种情况不符合题意;
当t<1时,h=2﹣t,则3(2﹣t)=18,解得t=﹣4.
故点F的坐标为(0,﹣4).
所以,点F的坐标为(0,7)或(0,﹣4).
第 1 页 共 6 页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
