人教版九年级上册数学 21.1 一元二次方程课件(18张ppt)
文档属性
| 名称 | 人教版九年级上册数学 21.1 一元二次方程课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 19:22:59 | ||
图片预览






文档简介
一元二次方程
教学目标:
1.了解一元二次方程的概念,能运用一元二次方程的概念解决简单问题;
2.掌握一元二次方程的一般形式ax2+bx+c=0
(a≠0)及有关概念;
3.会进行简单的一元二次方程的试解,理解方程解的概念。
教学重点:
1.一元二次方程的概念及其一般形式;
2.一元二次方程解的探索。
教学难点:
1.由实际问题引出一元二次方程;
2.准确认识一元二次方程的二次项和系数、一次项和系数、常数项。
预备知识
1.平方根的意义:如果x2=a,那么x= 。
例如:x2=5,则x=
2.完全平方式:式子 叫做完全平方式,并且 。
例如:x2+4x+ =(x+ )2,x2-8x+ =(x- )2
4
2
16
4
你还认识“老朋友”吗?
一元二次方程的概念
等号的两边都是整式,只含有一个未知数
① ②
(一元),未知数的最高次数是2(二次)
③
的方程,叫做一元二次方程。
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
一次项,
一次项系数
必
须
牢
记
二
次
项
系
数
不
为
0
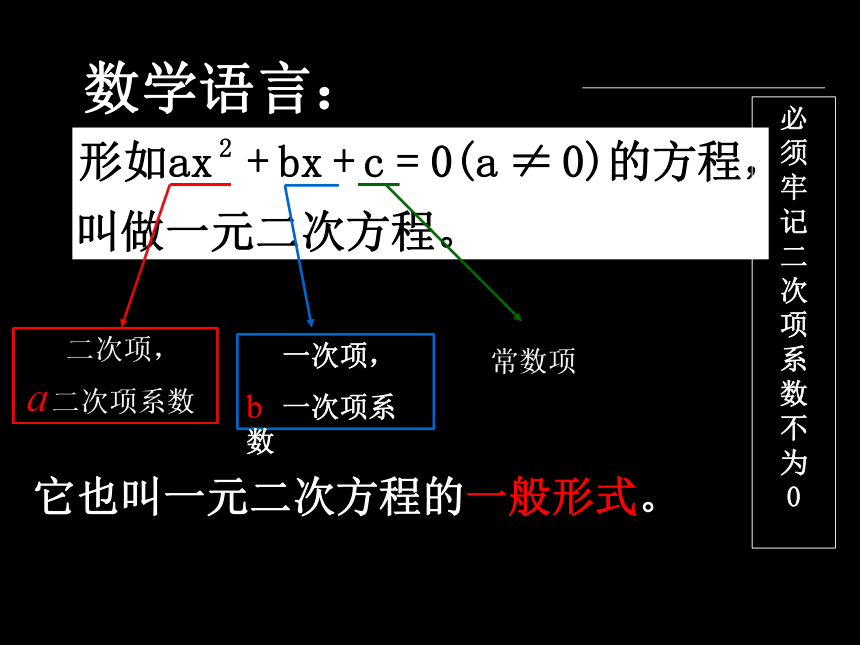
它也叫一元二次方程的一般形式。
数学语言:
b
?
例1.判断下列方程是否为一元二次方程?
×
×
×
×
×
×
√
√
√
√
例2.选择题
(1)方程(m-1)x2+mx+1=0为关于x的一元二次方程则m的值为___
A 任何实数 B m≠0 C m≠1 D m≠0 且m≠1
(2)关于x的方程中一定是一元二次方程的是( )
A. ax2+bx+c=0 B.
C
D
C.(m+1)x2=(m+1)2
D.(m2+1)x2-m2=0
考察一元二次方程的概念
又∵m-2≠0
∴m=-2
C
【分析】将已知x=0代入原方程的左右两边后,可以求出a的值,但是必须满足隐含条件“一元二次方程”,即保证二次项系数不能为零,这是我们容易忽略的地方。
知识纵横
x=-1
x=1
x=2
例6.已知关于x的方程(m-1)xm2+1 -3x+2=0是一元二次方程,则m的值为
例7.若一元二次方程ax2-bx-2015=0有一根为x=-1,则2a+2b=
例8.若x=1是方程x2+ax-b=0的解,
求 的值。
例9.已知m是方程x2+x-1=0的一个根,则2m2+2m+2016=( )
A. 2013 B. 2016 C. 2017 D.2018
D
-1
4030
-3
x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.07
A 3<x <3.23
C 3.24<x <3.25
D 3.25<x <3.26
B 3.23<x <3.24
C
C
【2019南京期中】形如x2+ax=b2的方程可用如图所示的图解法研究:画Rt△ABC,使∠ACB=90°,
AC=b,再在斜边AB上截取 则可以发现该方程的一个正根是线段 的长。
AD
D
C
B
A
b
【2020南京期中】若两个不同的方程x2+mx+1=0和x2+x+m=0有公共根,则常数m的值是 。
-2
解:设它们的公共根为t,则:
t2+mt+1=0 ①
t2+t+m=0 ②
①- ②得:
(m-1)t=m-1
若m=1,则两个方程均为x2+x+1=0,不符合题意。∴m≠1
当m≠1时,t=1,
把t=1代入 ②得:
m=-2。
已知m是方程x2-x-2=0的一个实数根,求代数式
的值。
4
课堂小结:
1.一元二次方程的概念以及怎样利用概念判断一元二次方程。
2.一元二次方程的一般形式ax2+bx+c=0(a≠0),特别强调a≠0。
3.要会判断一个数是否是一元二次方程的根。
符昊阳
教学目标:
1.了解一元二次方程的概念,能运用一元二次方程的概念解决简单问题;
2.掌握一元二次方程的一般形式ax2+bx+c=0
(a≠0)及有关概念;
3.会进行简单的一元二次方程的试解,理解方程解的概念。
教学重点:
1.一元二次方程的概念及其一般形式;
2.一元二次方程解的探索。
教学难点:
1.由实际问题引出一元二次方程;
2.准确认识一元二次方程的二次项和系数、一次项和系数、常数项。
预备知识
1.平方根的意义:如果x2=a,那么x= 。
例如:x2=5,则x=
2.完全平方式:式子 叫做完全平方式,并且 。
例如:x2+4x+ =(x+ )2,x2-8x+ =(x- )2
4
2
16
4
你还认识“老朋友”吗?
一元二次方程的概念
等号的两边都是整式,只含有一个未知数
① ②
(一元),未知数的最高次数是2(二次)
③
的方程,叫做一元二次方程。
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
一次项,
一次项系数
必
须
牢
记
二
次
项
系
数
不
为
0
它也叫一元二次方程的一般形式。
数学语言:
b
?
例1.判断下列方程是否为一元二次方程?
×
×
×
×
×
×
√
√
√
√
例2.选择题
(1)方程(m-1)x2+mx+1=0为关于x的一元二次方程则m的值为___
A 任何实数 B m≠0 C m≠1 D m≠0 且m≠1
(2)关于x的方程中一定是一元二次方程的是( )
A. ax2+bx+c=0 B.
C
D
C.(m+1)x2=(m+1)2
D.(m2+1)x2-m2=0
考察一元二次方程的概念
又∵m-2≠0
∴m=-2
C
【分析】将已知x=0代入原方程的左右两边后,可以求出a的值,但是必须满足隐含条件“一元二次方程”,即保证二次项系数不能为零,这是我们容易忽略的地方。
知识纵横
x=-1
x=1
x=2
例6.已知关于x的方程(m-1)xm2+1 -3x+2=0是一元二次方程,则m的值为
例7.若一元二次方程ax2-bx-2015=0有一根为x=-1,则2a+2b=
例8.若x=1是方程x2+ax-b=0的解,
求 的值。
例9.已知m是方程x2+x-1=0的一个根,则2m2+2m+2016=( )
A. 2013 B. 2016 C. 2017 D.2018
D
-1
4030
-3
x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.07
A 3<x <3.23
C 3.24<x <3.25
D 3.25<x <3.26
B 3.23<x <3.24
C
C
【2019南京期中】形如x2+ax=b2的方程可用如图所示的图解法研究:画Rt△ABC,使∠ACB=90°,
AC=b,再在斜边AB上截取 则可以发现该方程的一个正根是线段 的长。
AD
D
C
B
A
b
【2020南京期中】若两个不同的方程x2+mx+1=0和x2+x+m=0有公共根,则常数m的值是 。
-2
解:设它们的公共根为t,则:
t2+mt+1=0 ①
t2+t+m=0 ②
①- ②得:
(m-1)t=m-1
若m=1,则两个方程均为x2+x+1=0,不符合题意。∴m≠1
当m≠1时,t=1,
把t=1代入 ②得:
m=-2。
已知m是方程x2-x-2=0的一个实数根,求代数式
的值。
4
课堂小结:
1.一元二次方程的概念以及怎样利用概念判断一元二次方程。
2.一元二次方程的一般形式ax2+bx+c=0(a≠0),特别强调a≠0。
3.要会判断一个数是否是一元二次方程的根。
符昊阳
同课章节目录
