2020年秋人教版八年级数学上册随课练——12.3 角的平分线的性质拓展练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册随课练——12.3 角的平分线的性质拓展练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 482.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 19:56:26 | ||
图片预览


文档简介
12.3
角的平分线的性质拓展练习
一、选择题
1.点P在∠AOB的平分线上,点P到OA边的距离等于m,点Q是OB边上的一个动点,则PQ与m的大小关系是( )
A.PQ<m
B.PQ>m
C.PQ≤m
D.PQ≥m
2.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
3.如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB
B.与∠CBO互余的角有两个
C.∠AOB=90°
D.点O是CD的中点
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是(
)
A.PD=PE
B.OD=OE
C.∠DPO=∠EPO
D.PD=OP
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若AC=6,BC=8,则S△ABD:S△ACD为( )
A.5:3
B.5:4
C.4:3
D.3:5
6.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是( )
A.AD平分BC
B.AD平分∠CAB
C.AD平分∠CDB
D.AD⊥BC
7.已知:如图,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于H,若∠AFB=40°,∠BCF的度数为( )
A.40°
B.50°
C.55°
D.60°
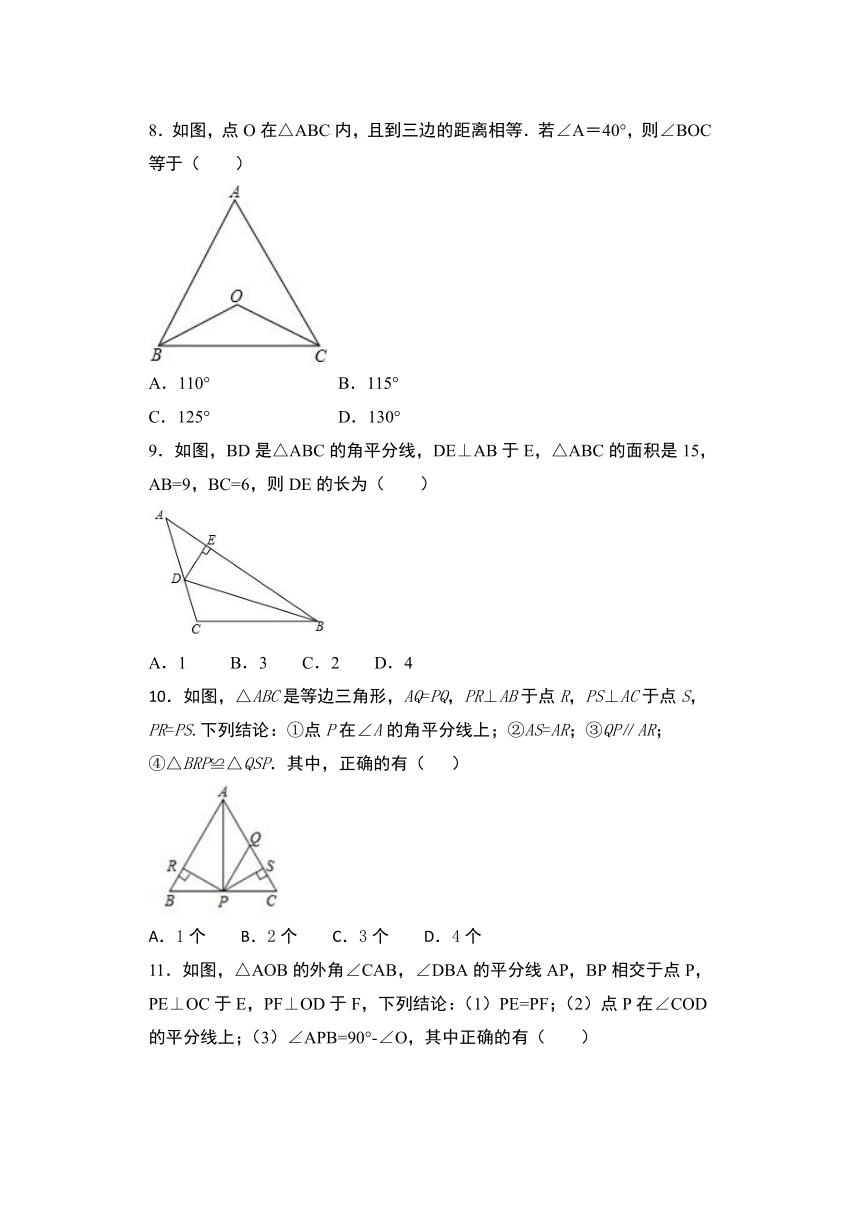
8.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于( )
A.110°
B.115°
C.125°
D.130°
9.如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为( )
A.1
B.3
C.2
D.4
10.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有(
)
A.1个
B.2个
C.3个
D.4个
11.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°-∠O,其中正确的有( )
A.0个
B.1个
C.2个
D.3个
二、填空题
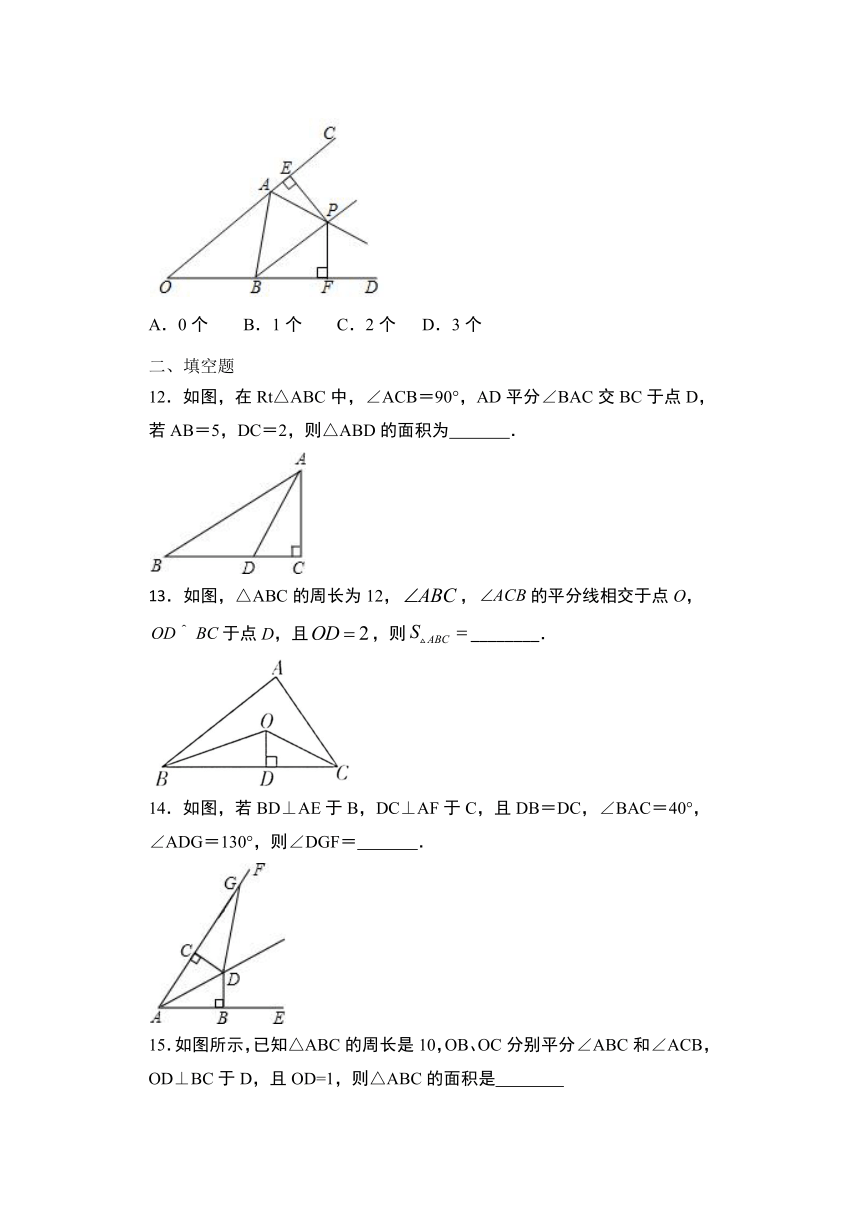
12.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若AB=5,DC=2,则△ABD的面积为
.
13.如图,△ABC的周长为12,,的平分线相交于点O,于点D,且,则________.
14.如图,若BD⊥AE于B,DC⊥AF于C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=
.
15.如图所示,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是
三、解答题
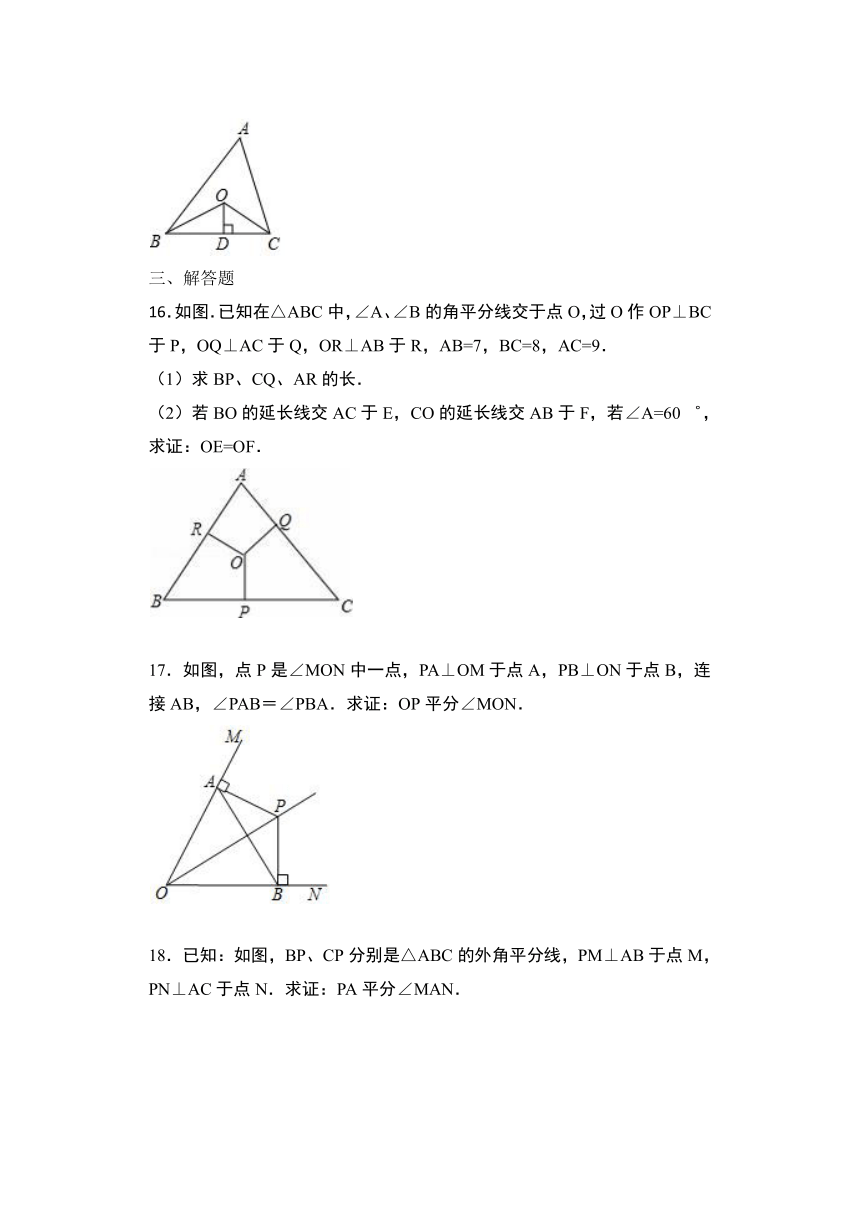
16.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
17.如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.求证:OP平分∠MON.
18.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
19.如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为
;请直接写出∠APD=
;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
20.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.
21.已知AB∥CD,点E为平面内一点,BE⊥CE于E,
(1)如图1,请直接写出∠ABE和∠DCE之间的数量关系;
(2)如图2,过点E作EF⊥CD,垂足为F,求证:∠CEF=∠ABE;
(3)如图3,在(2)的条件下,作EG平分∠CEF交DF于点G,作ED平分∠BEF交CD于D,连接BD,若∠DBE+∠ABD=180°,且∠BDE=3∠GEF,求∠BEG的度数.
答案
1.
D
2.
D
3.
B
4.
D
5.
A
6.
B
7.
B
8.
A
9.
C
10.
D
11.
C
12.
5
13.
12
14.
150°
15.
5
16.
解:连接AO,OB,OC,
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,AB=7,BC=8,AC=9,
则,
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N,
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中,
∠ONF=∠OME,ON=OM,∠FON=∠EOM,
∴△FON≌△EOM,
∴OE=OF.
17.
证明:∵∠PAB=∠PBA,
∴PA=PB,
∵PA⊥OM于点A,PB⊥ON于点B,
∴OP平分∠MON.
18.
作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19.
(1)解:如图1中,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMC=∠DMP,
∴∠APD=∠ACD=30°,
故答案为AE=BD,30°
(2)如图2中,结论:AE=BD,∠APD=30°.
理由:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMP=∠DMC,
∴∠APD=∠ACD=30°.
(3)如图2﹣1中,分别过C作CH⊥AE,垂足为H,过点C作CG⊥BD,垂足为G,
∵△ACE≌△DCB.
∴AE=BD,
∵S△ACE=S△DCB
∴CH=CG,
∴∠DPC=∠EPC
∵∠APD=∠BPE,
∴∠APC=∠BPC.
20.
(1)5;(2)6.25
21.
解:(1)结论:∠DCE=90°+∠ABE.
理由:如图1中,从BE交DC的延长线于H.
∵AB∥CH,
∴∠ABE=∠H,
∵BE⊥CE,
∴∠CEH=90°,
∴∠DCE=∠H+∠CEH=90°+∠H,
∴∠DCE=90°+∠ABE.
(2)如图2中,作EM∥CD,
∵EM∥CD,CD∥AB,
∴AB∥CD∥EM,
∴∠BEM=∠ABE,∠F+∠FEM=180°,
∵EF⊥CD,
∴∠F=90°,
∴∠FEM=90°,
∴∠CEF与∠CEM互余,
∵BE⊥CE,
∴∠BEC=90°,
∴∠BEM与∠CEM互余,
∴∠CEF=∠BEM,
∴∠CEF=∠ABE.
(3)如图3中,设∠GEF=α,∠EDF=β.
∴∠BDE=3∠GEF=3α,
∵EG平分∠CEF,
∴∠CEF=2∠FEG=2α,
∴∠ABE=∠CEF=2α,
∵AB∥CD∥EM,
∴∠MED=∠EDF=β,∠KBD=∠BDF=3α+β,∠ABD+∠BDF=180°,
∴∠BED=∠BEM+∠MED=2α+β,
∵ED平分∠BEF,
∴∠BED=∠FED=2α+β,
∴∠DEC=β,
∵∠BEC=90°,
∴2α+2β=90°,
∵∠DBE+∠ABD=180°,∠ABD+∠BDF=180°,
∴∠DBE=∠BDF=∠BDE+∠EDF=3α+β,
∵∠ABK=180°,
∴∠ABE+∠B=DBE+∠KBD=180°,
即2α+(3α+β)+(3α+β)=180°,
∴6α+(2α+2β)=180°,
∴α=15°,
∴∠BEG=∠BEC+∠CEG=90°+15°=105°.
角的平分线的性质拓展练习
一、选择题
1.点P在∠AOB的平分线上,点P到OA边的距离等于m,点Q是OB边上的一个动点,则PQ与m的大小关系是( )
A.PQ<m
B.PQ>m
C.PQ≤m
D.PQ≥m
2.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
3.如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB
B.与∠CBO互余的角有两个
C.∠AOB=90°
D.点O是CD的中点
4.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是(
)
A.PD=PE
B.OD=OE
C.∠DPO=∠EPO
D.PD=OP
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若AC=6,BC=8,则S△ABD:S△ACD为( )
A.5:3
B.5:4
C.4:3
D.3:5
6.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是( )
A.AD平分BC
B.AD平分∠CAB
C.AD平分∠CDB
D.AD⊥BC
7.已知:如图,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于H,若∠AFB=40°,∠BCF的度数为( )
A.40°
B.50°
C.55°
D.60°
8.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于( )
A.110°
B.115°
C.125°
D.130°
9.如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为( )
A.1
B.3
C.2
D.4
10.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有(
)
A.1个
B.2个
C.3个
D.4个
11.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°-∠O,其中正确的有( )
A.0个
B.1个
C.2个
D.3个
二、填空题
12.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若AB=5,DC=2,则△ABD的面积为
.
13.如图,△ABC的周长为12,,的平分线相交于点O,于点D,且,则________.
14.如图,若BD⊥AE于B,DC⊥AF于C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=
.
15.如图所示,已知△ABC的周长是10,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,则△ABC的面积是
三、解答题
16.如图.已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
(1)求BP、CQ、AR的长.
(2)若BO的延长线交AC于E,CO的延长线交AB于F,若∠A=60゜,求证:OE=OF.
17.如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.求证:OP平分∠MON.
18.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
19.如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为
;请直接写出∠APD=
;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
20.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.
21.已知AB∥CD,点E为平面内一点,BE⊥CE于E,
(1)如图1,请直接写出∠ABE和∠DCE之间的数量关系;
(2)如图2,过点E作EF⊥CD,垂足为F,求证:∠CEF=∠ABE;
(3)如图3,在(2)的条件下,作EG平分∠CEF交DF于点G,作ED平分∠BEF交CD于D,连接BD,若∠DBE+∠ABD=180°,且∠BDE=3∠GEF,求∠BEG的度数.
答案
1.
D
2.
D
3.
B
4.
D
5.
A
6.
B
7.
B
8.
A
9.
C
10.
D
11.
C
12.
5
13.
12
14.
150°
15.
5
16.
解:连接AO,OB,OC,
∵OP⊥BC,OQ⊥AC,OR⊥AB,∠A、∠B的角平分线交于点O,
∴OR=OQ,OR=OP,
∴由勾股定理得:AR2=OA2﹣OR2,AQ2=AO2﹣OQ2,
∴AR=AQ,
同理BR=BP,CQ=CP,
即O在∠ACB角平分线上,
设BP=BR=x,CP=CQ=y,AQ=AR=z,AB=7,BC=8,AC=9,
则,
x=3,y=5,z=4,
∴BP=3,CQ=5,AR=4.
(2)过O作OM⊥AC于M,ON⊥AB于N,
∵O在∠A的平分线,
∴OM=ON,∠ANO=∠AMO=90°,
∵∠A=60°,
∴∠NOM=120°,
∵O在∠ACB、∠ABC的角平分线上,
∴∠EBC+∠FCB=(∠ABC+∠ACB)=×(180°﹣∠A)=60°,
∴∠FON=∠EOM,
在△FON和△EOM中,
∠ONF=∠OME,ON=OM,∠FON=∠EOM,
∴△FON≌△EOM,
∴OE=OF.
17.
证明:∵∠PAB=∠PBA,
∴PA=PB,
∵PA⊥OM于点A,PB⊥ON于点B,
∴OP平分∠MON.
18.
作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
19.
(1)解:如图1中,
∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMC=∠DMP,
∴∠APD=∠ACD=30°,
故答案为AE=BD,30°
(2)如图2中,结论:AE=BD,∠APD=30°.
理由:∵∠ACD=∠BCE,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
又∵CA=CD,CE=CB,
∴△ACE≌△DCB.
∴AE=BD,∴CAE=∠CDB,
∵∠AMP=∠DMC,
∴∠APD=∠ACD=30°.
(3)如图2﹣1中,分别过C作CH⊥AE,垂足为H,过点C作CG⊥BD,垂足为G,
∵△ACE≌△DCB.
∴AE=BD,
∵S△ACE=S△DCB
∴CH=CG,
∴∠DPC=∠EPC
∵∠APD=∠BPE,
∴∠APC=∠BPC.
20.
(1)5;(2)6.25
21.
解:(1)结论:∠DCE=90°+∠ABE.
理由:如图1中,从BE交DC的延长线于H.
∵AB∥CH,
∴∠ABE=∠H,
∵BE⊥CE,
∴∠CEH=90°,
∴∠DCE=∠H+∠CEH=90°+∠H,
∴∠DCE=90°+∠ABE.
(2)如图2中,作EM∥CD,
∵EM∥CD,CD∥AB,
∴AB∥CD∥EM,
∴∠BEM=∠ABE,∠F+∠FEM=180°,
∵EF⊥CD,
∴∠F=90°,
∴∠FEM=90°,
∴∠CEF与∠CEM互余,
∵BE⊥CE,
∴∠BEC=90°,
∴∠BEM与∠CEM互余,
∴∠CEF=∠BEM,
∴∠CEF=∠ABE.
(3)如图3中,设∠GEF=α,∠EDF=β.
∴∠BDE=3∠GEF=3α,
∵EG平分∠CEF,
∴∠CEF=2∠FEG=2α,
∴∠ABE=∠CEF=2α,
∵AB∥CD∥EM,
∴∠MED=∠EDF=β,∠KBD=∠BDF=3α+β,∠ABD+∠BDF=180°,
∴∠BED=∠BEM+∠MED=2α+β,
∵ED平分∠BEF,
∴∠BED=∠FED=2α+β,
∴∠DEC=β,
∵∠BEC=90°,
∴2α+2β=90°,
∵∠DBE+∠ABD=180°,∠ABD+∠BDF=180°,
∴∠DBE=∠BDF=∠BDE+∠EDF=3α+β,
∵∠ABK=180°,
∴∠ABE+∠B=DBE+∠KBD=180°,
即2α+(3α+β)+(3α+β)=180°,
∴6α+(2α+2β)=180°,
∴α=15°,
∴∠BEG=∠BEC+∠CEG=90°+15°=105°.
