人教版初中数学八年级上册 12.3角的平分线的性质 课后提升训练试卷(Word版 含解析)
文档属性
| 名称 | 人教版初中数学八年级上册 12.3角的平分线的性质 课后提升训练试卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 390.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览


文档简介
2020年秋绵阳外国语学校
初中数学(人教版)八年级上册
第十二章 全等三角形
12.3 角的平分线的性质
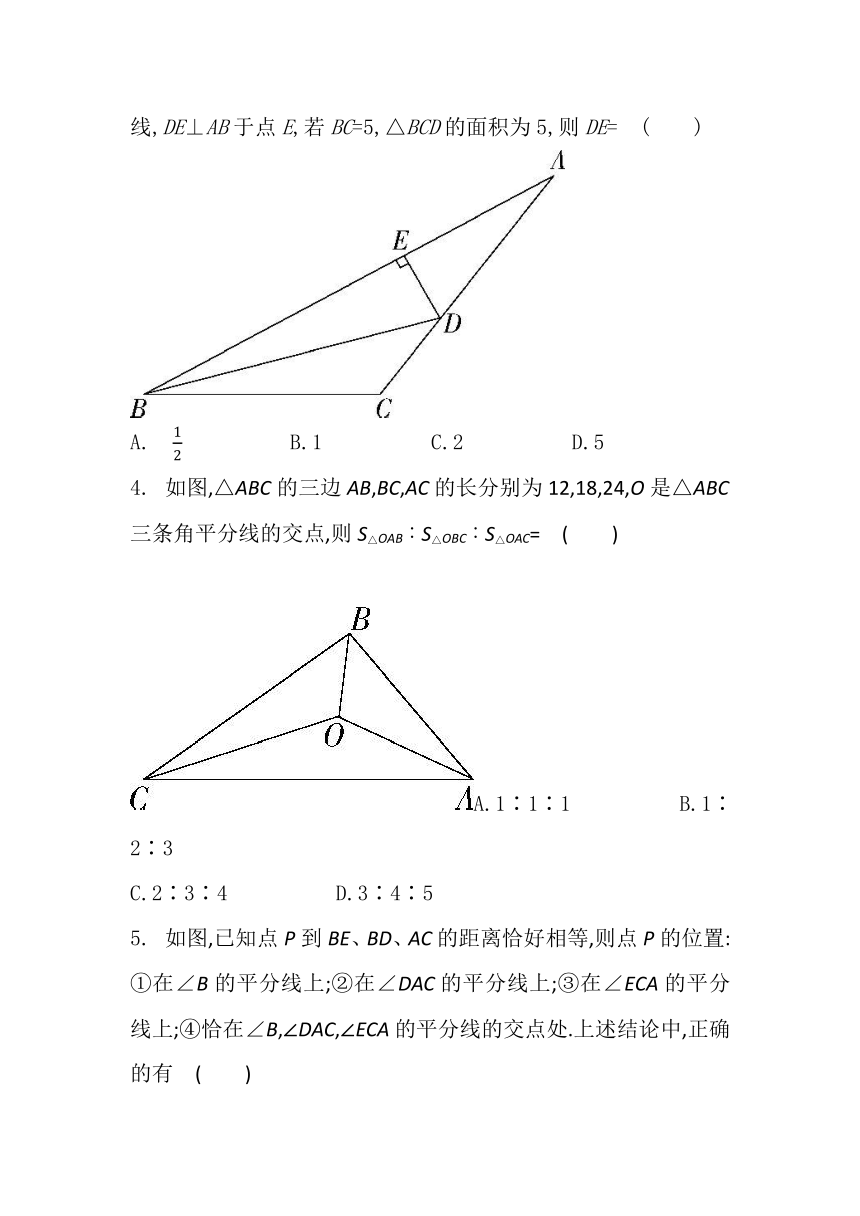
1.用直尺和圆规作已知角的平分线的示意图如图所示,则说明∠CAD=∠DAB的依据是?( )
?
A.SSS B.SAS C.ASA D.AAS
2.
如图2,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是?( )
?A.2 ????B.3 ????C.4 ????D.6
3.
(2019江苏南通海门期中)如图,BD是△ABC的角平分线,DE⊥AB于点E,若BC=5,△BCD的面积为5,则DE=?( )
A.? ????B.1 ????C.2 ????D.5
4.
如图,△ABC的三边AB,BC,AC的长分别为12,18,24,O是△ABC三条角平分线的交点,则S△OAB∶S△OBC∶S△OAC=?( )
?A.1∶1∶1 ????B.1∶2∶3 ????
C.2∶3∶4 ????D.3∶4∶5
5.
如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰在∠B,∠DAC,∠ECA的平分线的交点处.上述结论中,正确的有?( )
?
A.1个 ????B.2个 ????C.3个 ????D.4个
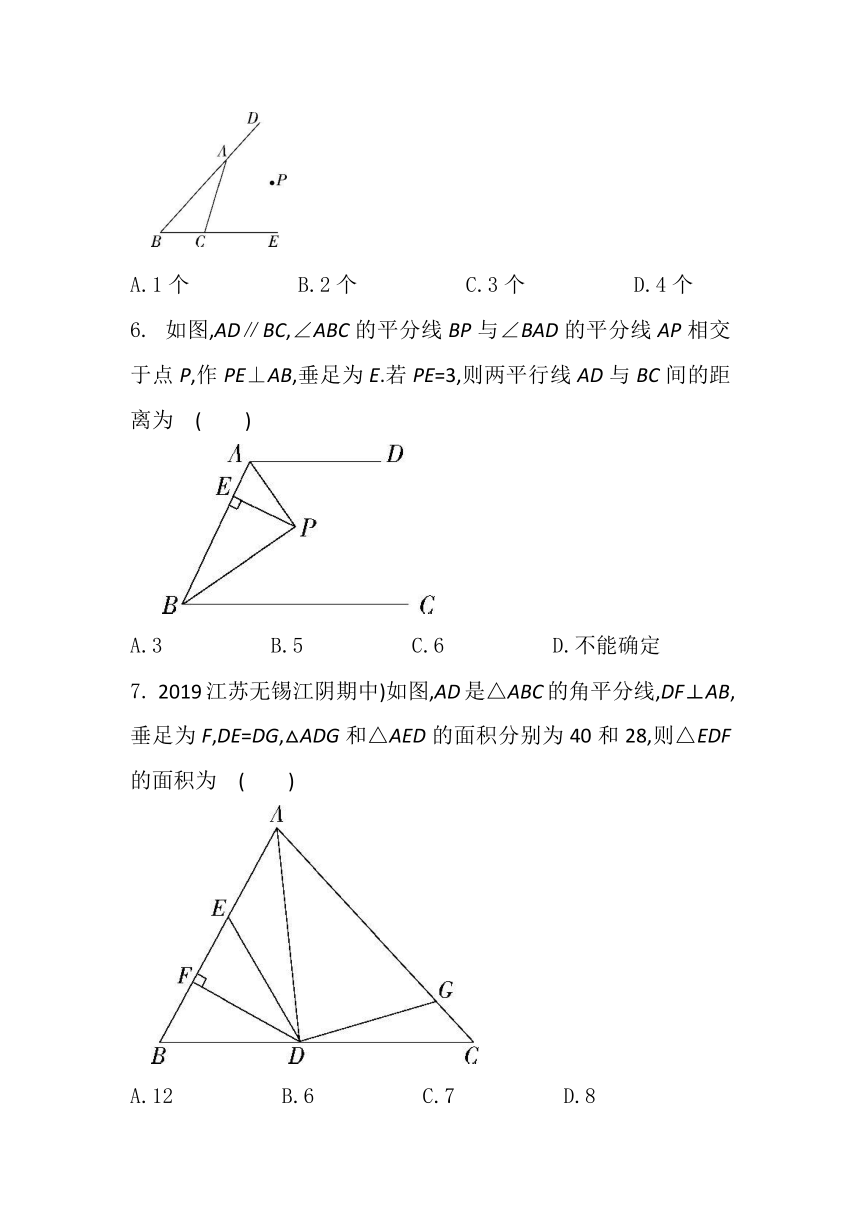
6.
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为?( )
?
A.3 ????B.5 ????C.6 ????D.不能确定
7.
2019江苏无锡江阴期中)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为?( )
?
A.12 ????B.6 ????C.7 ????D.8
8.
(2020湖北襄阳樊城期末)小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB,另一把直尺压住射线OA,并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是?( )
A.角的内部到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
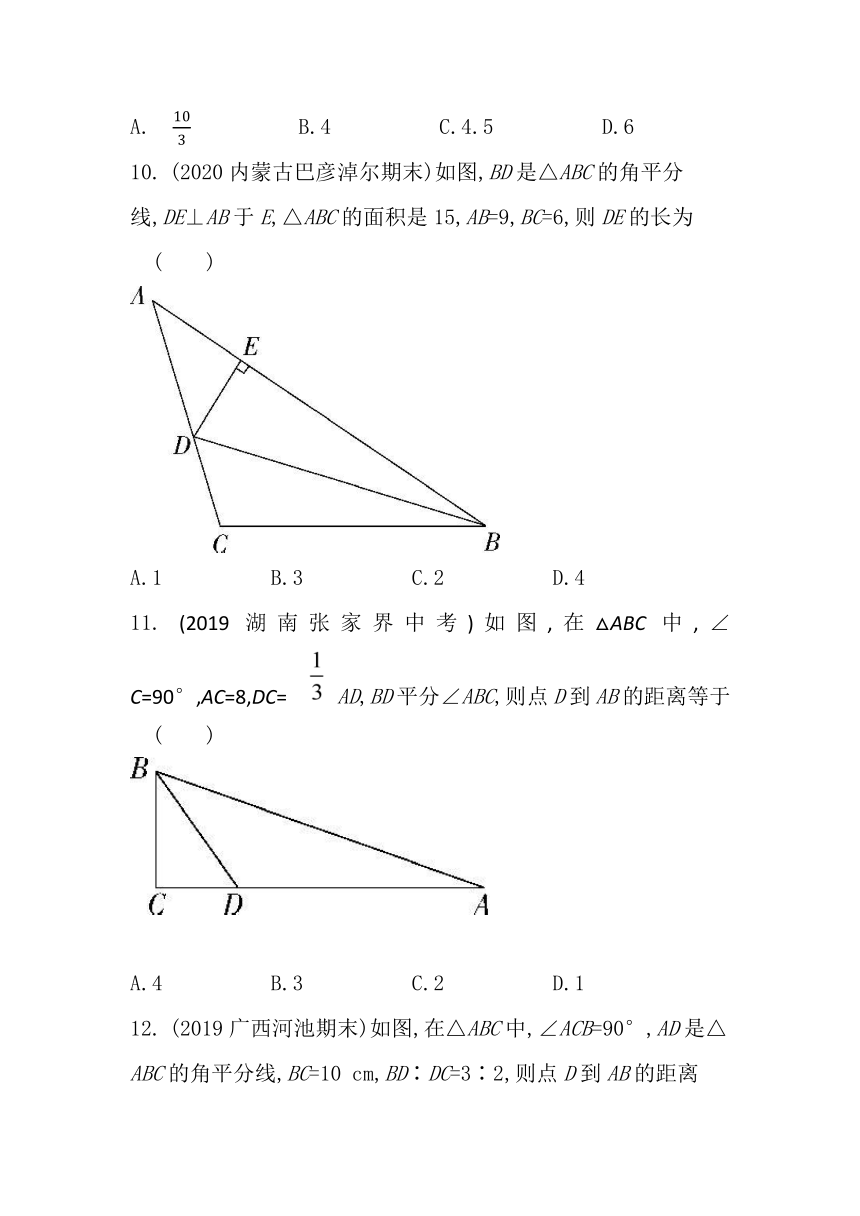
9.
(2020湖北武汉硚口期中)如图,在△ABC中,AD是它的角平分线,AB=9,AC=6,BC=10,则CD的长为?( )
?
A.? ????B.4 ????C.4.5 ????D.6
10.
(2020内蒙古巴彦淖尔期末)如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为?( )
A.1 ????B.3 ????C.2 ????D.4
11.
(2019湖南张家界中考)如图,在△ABC中,∠C=90°,AC=8,DC=?
AD,BD平分∠ABC,则点D到AB的距离等于?( )
A.4 ????B.3 ????C.2 ????D.1
12.
(2019广西河池期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10
cm,BD∶DC=3∶2,则点D到AB的距离为 ????.
13.
如图,PM⊥OA,PN⊥OB,垂足分别为点M,N,PM=PN,∠BOC=30°,则∠AOB= ????.
14.
.如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF= ????.
15.
如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于点E.若BC=5
cm,DC=4
cm,则△DEB的周长为 ????cm.
16.
(2020辽宁葫芦岛连山期中)如图,AD平分∠BAC,BD平分∠ABC,DE⊥AB,E为垂足,△ABC的周长为20
cm,面积为40
cm2,则DE的长为 ????????.
17.
如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE=FC,求证:BD=DF.
18.
如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.求证:AD平分∠BAC.
19.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
20.
如图,在△ABC中,∠B=∠C,D是BC边上的动点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.当点D移动到什么位置时,AD恰好平分∠BAC?请说明理由.
?
21.
本节课我们知道了角平分线有以下性质:角平分线上的点到角的两边的距离相等.从而小芳产生了以下的想法:如图,已知△ABC中,AD平分∠BAC,那么AB∶AC=BD∶CD成立吗?若成立,请尝试证明.
22.
如图所示,在△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.
?
参考答案
1.
答案????A 从角平分线的作法得出,△AFD与△AED的三边对应相等,则△AFD≌△AED(SSS),所以∠CAD=∠DAB.故选A.
2.
答案?D
∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,
∴DF=DE=6,故选D
3.
答案????C 如图,作DF⊥BC交BC的延长线于点F.
?
∵BC=5,△BCD的面积为5,∴?BC·DF=5,
即?×5·DF=5,∴DF=2,∵BD平分∠ABC,
DE⊥AB,DF⊥BC,∴DE=DF=2,故选C.
4.
答案????C????∵O是△ABC三条角平分线的交点,AB,BC,AC的长分别为12,18,24,
∴S△OAB∶S△OBC∶S△OAC=AB∶CB∶AC=12∶18∶24=2∶3∶4.故选C.
5.
答案????D 由点P到BE、BD、AC的距离恰好相等和角平分线的判定可知①②③④都是正确的.
6.
答案????C 如图,作PF⊥AD于点F,反向延长PF,与BC交于点G,∵AD∥BC,PF⊥AD,
∴∠PGC=90°,即PG⊥BC.
∴两平行线AD与BC间的距离为FG的长.
∵AP平分∠BAD,PF⊥AD,PE⊥AB,
∴PF=PE=3,
∵BP平分∠ABC,PE⊥AB,PG⊥BC,
∴PG=PE=3,
∴FG=PF+PG=6.
7.
答案????B 如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH.在Rt△DEF和Rt△DGH中,?
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,同理Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH.
设△EDF的面积为S,则△GDH的面积为S,
则28+S=40-S,
解得S=6.故选B.
8.
答案????A 如图所示,过两把直尺的交点P作PE⊥AO,PF⊥BO,∵两把长方形直尺完全相同,∴PE=PF,又PE⊥AO,PF⊥BO,∴OP平分∠AOB,依据是角的内部到角的两边距离相等的点在角的平分线上,故选A.
9.
答案????B 如图,作DE⊥AB于E,DF⊥AC于F,
∵AD平分∠BAC,
∴DE=DF,
10.
答案????C 如图,作DF⊥BC交BC的延长线于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,∴DE=DF.由题意得?AB·DE+?BC·DF=15,
即?×9DE+?×6DE=15,
解得DE=2,故选C.
11.
答案????C 如图,过点D作DE⊥AB于点E,
∵∠C=90°,BD平分∠ABC,DE⊥AB,
∴DE=CD=2,
即点D到AB的距离为2.故选C.
12.
答案????4
cm
解析????∵BC=10
cm,BD∶DC=3∶2,
∴DC=4
cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC的长,
即点D到AB的距离等于4
cm.
13.
答案 60°
解析 ∵PM⊥OA,PN⊥OB,PM=PN,
∴OC平分∠AOB,即∠AOC=∠BOC=30°,
∴∠AOB=60°.
14.
答案 150°
解析 ∵DB⊥AE,DC⊥AF,且DB=DC,
∴AD平分∠BAC,
∵∠BAC=40°,∴∠CAD=?∠BAC=20°,
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
15.
答案 5
解析 ∵CD平分∠ACB,DE⊥BC,∠A=90°,∴DE=DA.
在Rt△CDE和Rt△CDA中,?
∴Rt△CDE≌Rt△CDA,∴CE=CA,
∴△DEB的周长=BE+BD+DE=BE+BD+DA=BE+BA
=BE+AC=BE+CE=BC=5
cm.
16.
答案????4
cm
解析 如图,连接CD,∵AD平分∠BAC,BD平分∠ABC,∴点D到AC,AB,BC的距离相等,距离都等于DE的长,
∵△ABC的周长为20
cm,面积为40
cm2,
∴S△ABC=S△ADC+S△CDB+S△ADB=?AC·DE+?BC·DE+?AB·DE
=?
(AC+BC+AB)·DE=40,即
40=?×20DE,
∴DE=4
cm.
?
17.
证明????∵AD平分∠CAB,DE⊥AB,∠C=90°,∴DE=DC.
在△BDE和△FDC中,?
∴△BDE≌△FDC,∴BD=DF.
18.
证明????∵DF⊥AC,DE⊥AB,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,?
∴△BDE≌△CDF(AAS),
∴DE=DF.∴AD平分∠BAC.
19.
证明 ∵点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,
∴∠BEO=∠CDO=90°,OE=OD.
在△BEO和△CDO中,
∵?
∴△BEO≌△CDO(ASA),
∴OB=OC.
20.
解析 当点D移动到BC的中点时,AD恰好平分∠BAC.
理由:当D是BC的中点时,BD=CD.
∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°.
又∵∠B=∠C,BD=CD,
∴△DEB≌△DFC(AAS).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
21.
解析 成立.证明:在图1中作DE⊥AB,DF⊥AC,垂足分别为E,F,∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=?AB·DE,S△ACD=?AC·DF,
∴S△ABD∶S△ACD=AB∶AC.
在图2中作AP⊥BC,垂足为P,
∵S△ABD=?BD·AP,S△ACD=?CD·AP,
∴S△ABD∶S△ACD=BD∶CD.
∴AB∶AC=BD∶CD.
22.
证明????如图,过D作DE⊥AB于E,DF⊥AC于F,
则∠BED=∠CFD=90°.
?
在△BED和△CFD中,?
∴△BED≌△CFD(AAS).
∴DE=DF,∴AD平分∠BAC.
初中数学(人教版)八年级上册
第十二章 全等三角形
12.3 角的平分线的性质
1.用直尺和圆规作已知角的平分线的示意图如图所示,则说明∠CAD=∠DAB的依据是?( )
?
A.SSS B.SAS C.ASA D.AAS
2.
如图2,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是?( )
?A.2 ????B.3 ????C.4 ????D.6
3.
(2019江苏南通海门期中)如图,BD是△ABC的角平分线,DE⊥AB于点E,若BC=5,△BCD的面积为5,则DE=?( )
A.? ????B.1 ????C.2 ????D.5
4.
如图,△ABC的三边AB,BC,AC的长分别为12,18,24,O是△ABC三条角平分线的交点,则S△OAB∶S△OBC∶S△OAC=?( )
?A.1∶1∶1 ????B.1∶2∶3 ????
C.2∶3∶4 ????D.3∶4∶5
5.
如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰在∠B,∠DAC,∠ECA的平分线的交点处.上述结论中,正确的有?( )
?
A.1个 ????B.2个 ????C.3个 ????D.4个
6.
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为?( )
?
A.3 ????B.5 ????C.6 ????D.不能确定
7.
2019江苏无锡江阴期中)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为?( )
?
A.12 ????B.6 ????C.7 ????D.8
8.
(2020湖北襄阳樊城期末)小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB,另一把直尺压住射线OA,并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的平分线.”他这样做的依据是?( )
A.角的内部到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
9.
(2020湖北武汉硚口期中)如图,在△ABC中,AD是它的角平分线,AB=9,AC=6,BC=10,则CD的长为?( )
?
A.? ????B.4 ????C.4.5 ????D.6
10.
(2020内蒙古巴彦淖尔期末)如图,BD是△ABC的角平分线,DE⊥AB于E,△ABC的面积是15,AB=9,BC=6,则DE的长为?( )
A.1 ????B.3 ????C.2 ????D.4
11.
(2019湖南张家界中考)如图,在△ABC中,∠C=90°,AC=8,DC=?
AD,BD平分∠ABC,则点D到AB的距离等于?( )
A.4 ????B.3 ????C.2 ????D.1
12.
(2019广西河池期末)如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10
cm,BD∶DC=3∶2,则点D到AB的距离为 ????.
13.
如图,PM⊥OA,PN⊥OB,垂足分别为点M,N,PM=PN,∠BOC=30°,则∠AOB= ????.
14.
.如图,已知DB⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF= ????.
15.
如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于点E.若BC=5
cm,DC=4
cm,则△DEB的周长为 ????cm.
16.
(2020辽宁葫芦岛连山期中)如图,AD平分∠BAC,BD平分∠ABC,DE⊥AB,E为垂足,△ABC的周长为20
cm,面积为40
cm2,则DE的长为 ????????.
17.
如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE=FC,求证:BD=DF.
18.
如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.求证:AD平分∠BAC.
19.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
20.
如图,在△ABC中,∠B=∠C,D是BC边上的动点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.当点D移动到什么位置时,AD恰好平分∠BAC?请说明理由.
?
21.
本节课我们知道了角平分线有以下性质:角平分线上的点到角的两边的距离相等.从而小芳产生了以下的想法:如图,已知△ABC中,AD平分∠BAC,那么AB∶AC=BD∶CD成立吗?若成立,请尝试证明.
22.
如图所示,在△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.
?
参考答案
1.
答案????A 从角平分线的作法得出,△AFD与△AED的三边对应相等,则△AFD≌△AED(SSS),所以∠CAD=∠DAB.故选A.
2.
答案?D
∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,
∴DF=DE=6,故选D
3.
答案????C 如图,作DF⊥BC交BC的延长线于点F.
?
∵BC=5,△BCD的面积为5,∴?BC·DF=5,
即?×5·DF=5,∴DF=2,∵BD平分∠ABC,
DE⊥AB,DF⊥BC,∴DE=DF=2,故选C.
4.
答案????C????∵O是△ABC三条角平分线的交点,AB,BC,AC的长分别为12,18,24,
∴S△OAB∶S△OBC∶S△OAC=AB∶CB∶AC=12∶18∶24=2∶3∶4.故选C.
5.
答案????D 由点P到BE、BD、AC的距离恰好相等和角平分线的判定可知①②③④都是正确的.
6.
答案????C 如图,作PF⊥AD于点F,反向延长PF,与BC交于点G,∵AD∥BC,PF⊥AD,
∴∠PGC=90°,即PG⊥BC.
∴两平行线AD与BC间的距离为FG的长.
∵AP平分∠BAD,PF⊥AD,PE⊥AB,
∴PF=PE=3,
∵BP平分∠ABC,PE⊥AB,PG⊥BC,
∴PG=PE=3,
∴FG=PF+PG=6.
7.
答案????B 如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH.在Rt△DEF和Rt△DGH中,?
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,同理Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH.
设△EDF的面积为S,则△GDH的面积为S,
则28+S=40-S,
解得S=6.故选B.
8.
答案????A 如图所示,过两把直尺的交点P作PE⊥AO,PF⊥BO,∵两把长方形直尺完全相同,∴PE=PF,又PE⊥AO,PF⊥BO,∴OP平分∠AOB,依据是角的内部到角的两边距离相等的点在角的平分线上,故选A.
9.
答案????B 如图,作DE⊥AB于E,DF⊥AC于F,
∵AD平分∠BAC,
∴DE=DF,
10.
答案????C 如图,作DF⊥BC交BC的延长线于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,∴DE=DF.由题意得?AB·DE+?BC·DF=15,
即?×9DE+?×6DE=15,
解得DE=2,故选C.
11.
答案????C 如图,过点D作DE⊥AB于点E,
∵∠C=90°,BD平分∠ABC,DE⊥AB,
∴DE=CD=2,
即点D到AB的距离为2.故选C.
12.
答案????4
cm
解析????∵BC=10
cm,BD∶DC=3∶2,
∴DC=4
cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC的长,
即点D到AB的距离等于4
cm.
13.
答案 60°
解析 ∵PM⊥OA,PN⊥OB,PM=PN,
∴OC平分∠AOB,即∠AOC=∠BOC=30°,
∴∠AOB=60°.
14.
答案 150°
解析 ∵DB⊥AE,DC⊥AF,且DB=DC,
∴AD平分∠BAC,
∵∠BAC=40°,∴∠CAD=?∠BAC=20°,
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
15.
答案 5
解析 ∵CD平分∠ACB,DE⊥BC,∠A=90°,∴DE=DA.
在Rt△CDE和Rt△CDA中,?
∴Rt△CDE≌Rt△CDA,∴CE=CA,
∴△DEB的周长=BE+BD+DE=BE+BD+DA=BE+BA
=BE+AC=BE+CE=BC=5
cm.
16.
答案????4
cm
解析 如图,连接CD,∵AD平分∠BAC,BD平分∠ABC,∴点D到AC,AB,BC的距离相等,距离都等于DE的长,
∵△ABC的周长为20
cm,面积为40
cm2,
∴S△ABC=S△ADC+S△CDB+S△ADB=?AC·DE+?BC·DE+?AB·DE
=?
(AC+BC+AB)·DE=40,即
40=?×20DE,
∴DE=4
cm.
?
17.
证明????∵AD平分∠CAB,DE⊥AB,∠C=90°,∴DE=DC.
在△BDE和△FDC中,?
∴△BDE≌△FDC,∴BD=DF.
18.
证明????∵DF⊥AC,DE⊥AB,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,?
∴△BDE≌△CDF(AAS),
∴DE=DF.∴AD平分∠BAC.
19.
证明 ∵点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,
∴∠BEO=∠CDO=90°,OE=OD.
在△BEO和△CDO中,
∵?
∴△BEO≌△CDO(ASA),
∴OB=OC.
20.
解析 当点D移动到BC的中点时,AD恰好平分∠BAC.
理由:当D是BC的中点时,BD=CD.
∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°.
又∵∠B=∠C,BD=CD,
∴△DEB≌△DFC(AAS).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
21.
解析 成立.证明:在图1中作DE⊥AB,DF⊥AC,垂足分别为E,F,∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=?AB·DE,S△ACD=?AC·DF,
∴S△ABD∶S△ACD=AB∶AC.
在图2中作AP⊥BC,垂足为P,
∵S△ABD=?BD·AP,S△ACD=?CD·AP,
∴S△ABD∶S△ACD=BD∶CD.
∴AB∶AC=BD∶CD.
22.
证明????如图,过D作DE⊥AB于E,DF⊥AC于F,
则∠BED=∠CFD=90°.
?
在△BED和△CFD中,?
∴△BED≌△CFD(AAS).
∴DE=DF,∴AD平分∠BAC.
