人教版初中数学九年级上册22.1.4二次函数y=ax2+bx+c第的图象和性质课后提升训练试卷(含解析)
文档属性
| 名称 | 人教版初中数学九年级上册22.1.4二次函数y=ax2+bx+c第的图象和性质课后提升训练试卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 162.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览

文档简介
2020年秋绵阳南山双语学校
初中数学(人教版)九年级
上册
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c第的图象和性质
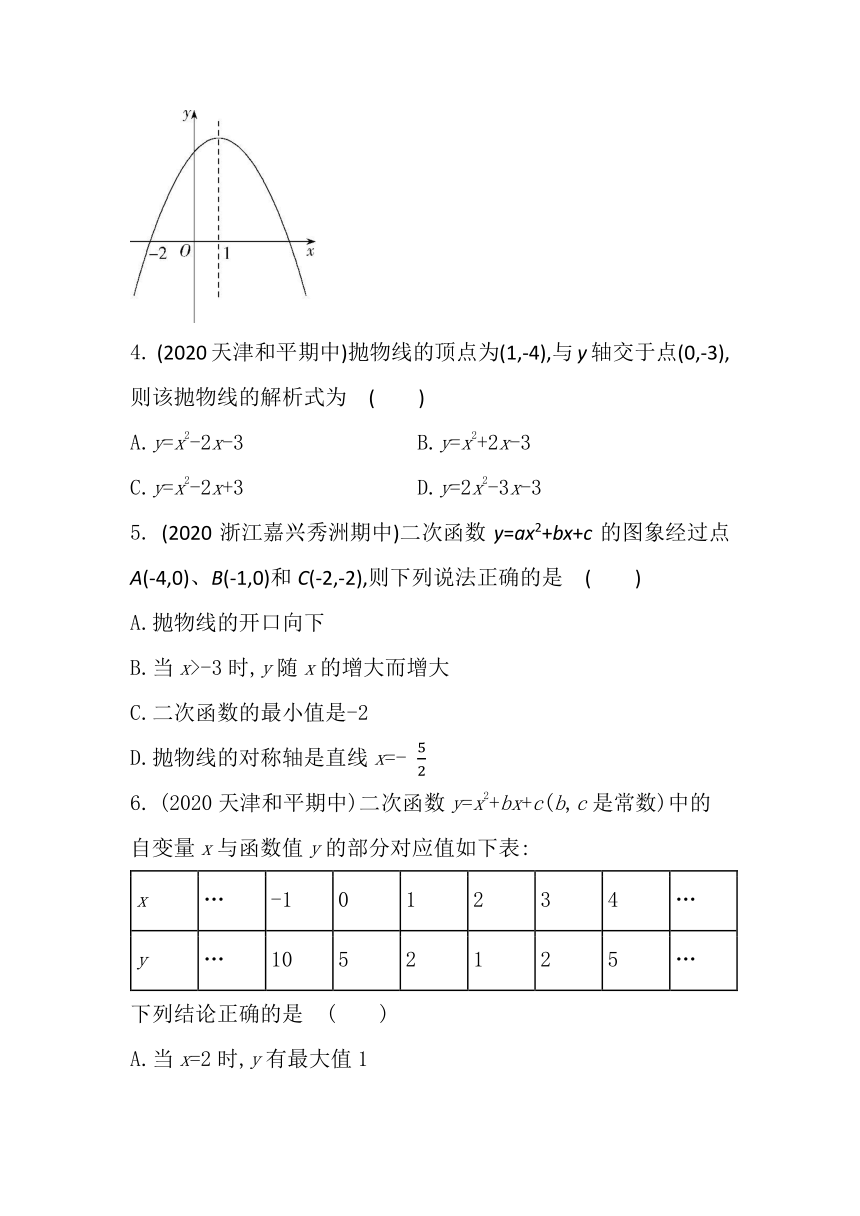
1.(2020湖北十堰丹江口期中)关于抛物线y=x2-2x-1,下列说法中错误的是?( )
A.开口方向向上
B.对称轴是直线x=1
C.当x>1时,y随x的增大而减小
D.顶点坐标为(1,-2)
2.(2019吉林四平铁西期中)二次函数y=-2x2-3x+1的图象大致是?( )
3.
(2020重庆八中月考)如图,已知抛物线y=ax2+bx+c(a≠0)经过点(-2,0),对称轴为直线x=1,下列结论中正确的是?( )
A.abc>0 ????B.b=2a
C.9a+3b+c<0 ????D.8a+c=0
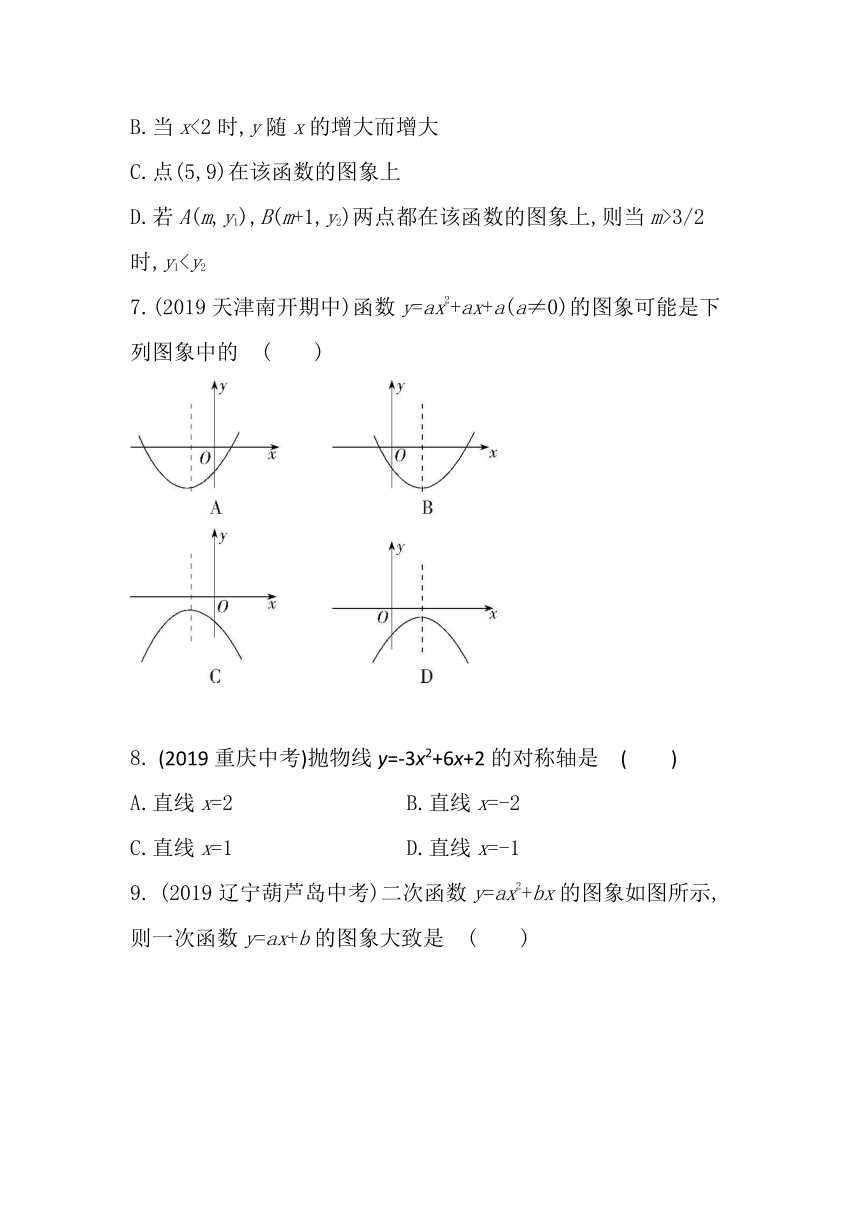
4.
(2020天津和平期中)抛物线的顶点为(1,-4),与y轴交于点(0,-3),则该抛物线的解析式为?( )
A.y=x2-2x-3 ????B.y=x2+2x-3
C.y=x2-2x+3 ????D.y=2x2-3x-3
5.
(2020浙江嘉兴秀洲期中)二次函数y=ax2+bx+c的图象经过点A(-4,0)、B(-1,0)和C(-2,-2),则下列说法正确的是?( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴是直线x=-
?
6.
(2020天津和平期中)二次函数y=x2+bx+c(b,c是常数)中的自变量x与函数值y的部分对应值如下表:
x
…
-1
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
下列结论正确的是?( )
A.当x=2时,y有最大值1
B.当x<2时,y随x的增大而增大
C.点(5,9)在该函数的图象上
D.若A(m,y1),B(m+1,y2)两点都在该函数的图象上,则当m>3/2?时,y17.(2019天津南开期中)函数y=ax2+ax+a(a≠0)的图象可能是下列图象中的?( )
8.
(2019重庆中考)抛物线y=-3x2+6x+2的对称轴是?( )
A.直线x=2 ????B.直线x=-2
C.直线x=1 ????D.直线x=-1
9.
(2019辽宁葫芦岛中考)二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象大致是?( )
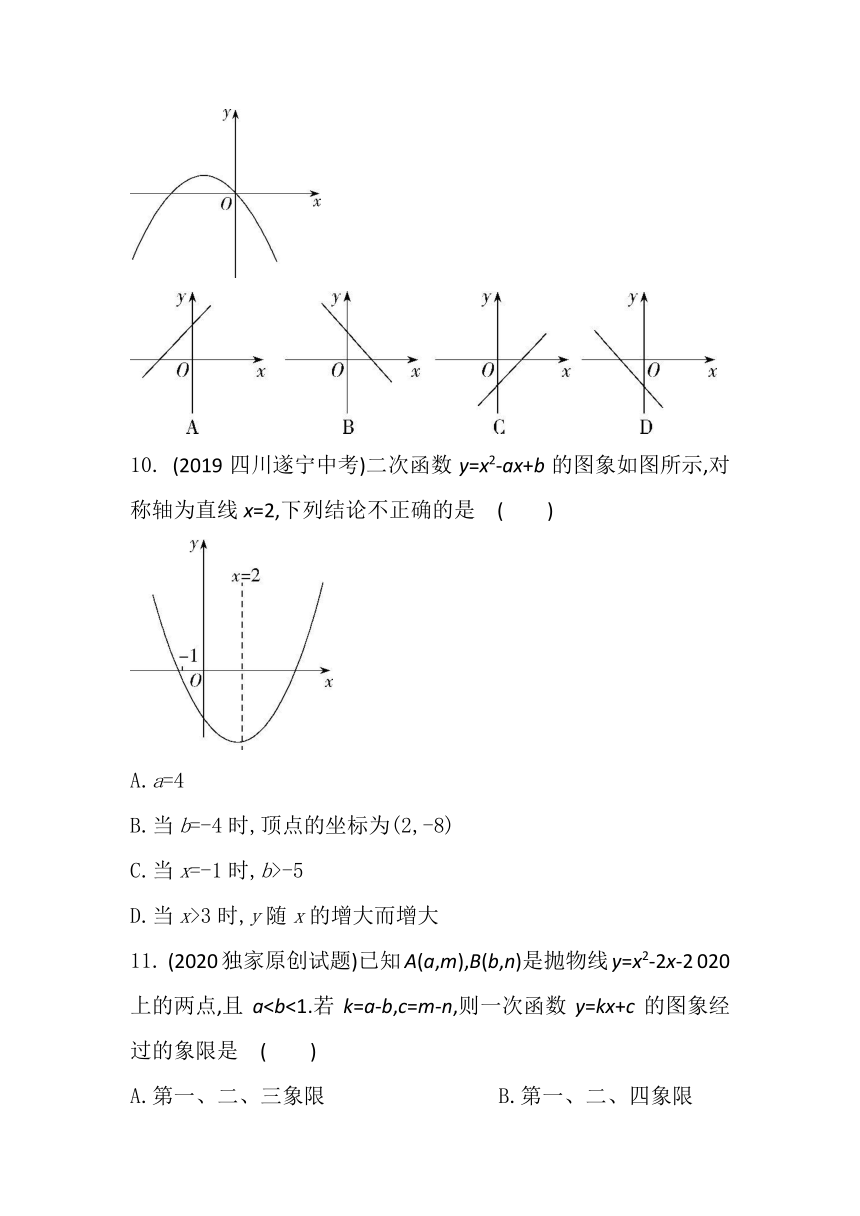
10.
(2019四川遂宁中考)二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是?( )
A.a=4
B.当b=-4时,顶点的坐标为(2,-8)
C.当x=-1时,b>-5
D.当x>3时,y随x的增大而增大
11.
(2020独家原创试题)已知A(a,m),B(b,n)是抛物线y=x2-2x-2
020上的两点,且aA.第一、二、三象限 ????B.第一、二、四象限
C.第二、三、四象限 ????D.第一、三、四象限
12.
(2019江苏徐州铜山二模)二次函数y=x2+2x+2的图象先向上平移2个单位长度,再向右平移3个单位长度,则平移后二次函数图象的顶点坐标是 ????.
13.
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在第 ????象限.
14.
(2020山东青岛莱西期中)顶点为(-6,0),开口向下,形状与函数y=
x2的图象相同的抛物线的表达式是 ????.
15.
(2019北京西城期中)已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中自变量x与函数值y之间满足下面的对应关系:
x
…
3
5
7
…
y
…
2.5
2.5
-1.5
…
则a+b+c= ????.
16.
(2020重庆巴南期中)已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x
0
1
2
y
4
3
4
若一次函数y=bx+ac的图象不经过第m象限,则m= ????
17.
(2020湖北孝感孝南期中)如图,抛物线y=ax2+bx+c的图象经过(-1,0),对称轴为x=1,则下列三个结论:
①abc<0;②10a+3b+c>0;③am2+bm+a≥0,其中正确的结论为 ???? ????(填序号).
18.
(2019福建莆田秀屿月考)若函数y=a(x-h)2+k的图象经过原点,最小值为-8且形状与抛物线y=-2x2-2x+3相同,则此函数关系式为????.
19.
(2020北京三十九中期中)把抛物线y=-x2+4x-3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是 ????.
20.
(2019福建龙岩上杭月考)如图,二次函数图象过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式.
21.
(2019山东淄博临淄期中)已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
x
…
-1
0
1
2
4
…
y
…
10
1
-2
1
25
…
(1)求这个二次函数的解析式;
(2)写出这个二次函数图象的顶点坐标.
参考答案
1.
答案????C
∵a=1>0,∴开口方向向上,故A说法正确;对称轴是
故B说法正确;当x>1时,y随x的增大而增大,故C说法错误;y=x2-2x-1=(x-1)2-2,顶点坐标为(1,-2),故D说法正确.故选C.
2.
答案????B
因为a=-2<0,所以抛物线y=-2x2-3x+1开口向下,故C、D不符合题意;抛物线y=-2x2-3x+1的对称轴是直线
故A不符合题意.故选B.
3.
答案????D ∵抛物线开口向下,∴a<0,∵抛物线对称轴为直线x=1,∴-b/2a?=1,∴b=-2a>0,故B错误;∵抛物线与y轴的正半轴相交,∴c>0,∴abc<0,故A错误;∵对称轴为直线x=1,又点(-2,0)关于直线x=1的对称点的坐标为(4,0),∴当x=3时,y=9a+3b+c>0,故C错误;∵抛物线y=ax2+bx+c经过点(-2,0),∴4a-2b+c=0,∵b=-2a,∴4a+4a+c=0,即8a+c=0,故D正确.故选D.
4.
答案????A 设抛物线的解析式为y=a(x-1)2-4,将(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4,解得a=1,∴抛物线的解析式为y=(x-1)2-4=x2-2x-3.故选A.
5.
答案????D ∵二次函数y=ax2+bx+c的图象经过点A(-4,0)、B(-1,0)和C(-2,-2),∴a>0,∴抛物线开口向上,故A错误;对称轴为直线
y随x的增大而增大,故B错误,D正确;
∴函数的最小值小于-2,故C错误.故选D.
6.
答案????D 观察表格知,函数的图象经过点(1,2)和(3,2),∴对称轴为x=2.∵函数图象开口向上且经过点(2,1),∴x=2时,y有最小值1,故A错误.易知当x<2时,y随x的增大而减小,故B错误.∵对称轴是直线x=2,点(-1,10)关于x=2的对称点是(5,10),∴点(5,10)在该函数的图象上,点(5,9)不在该函数的图象上,故C错误.∵当m>3/2?时,|2-m|<|m+1-2|,∴y17.
答案????C 在函数y=ax2+ax+a(a≠0)中,当a<0时,该函数图象开口向下,顶点在y轴左侧,抛物线与y轴的负半轴相交,故C正确、D错误;当a>0时,该函数图象开口向上,顶点在y轴左侧,抛物线与y轴的正半轴相交,故A、B错误.故选C.
8.
答案????C
9.
答案????D
10.
答案????C 由题意得,对称轴为直线x=2,∴a=4,故A正确;当b=-4时,y=x2-4x-4=(x-2)2-8,∴顶点的坐标为(2,-8),故B正确;当x=-1时,由图象知此时y<0,即1+4+b<0,∴b<-5,故C不正确;∵对称轴为直线x=2且图象开口向上,∴当x>3时,y随x的增大而增大,故D正确.故选C.
11.
答案????B????y=x2-2x-2
020=(x-1)2-2
021,∴抛物线开口向上,对称轴为x=1,当x<1时,y随x的增大而减小.∵A(a,m),B(b,n)是抛物线y=x2-2x-2
020上的两点,且an.∵k=a-b<0,c=m-n>0,∴一次函数y=kx+c的图象经过的象限是第一、二、四象限.故选B.
12.
答案 (2,3)
∵y=x2+2x+2=(x+1)2+1,顶点为(-1,1),
∴将图象向上平移2个单位长度,
再向右平移3个单位长度,平移后的二次函数图象的顶点坐标为(2,3).
13.
答案 一
14.
解析????设所求的抛物线的表达式为y=a(x-h)2+k,∵顶点为(-6,0),∴h=-6,k=0,又∵开口向下,形状与函数y=?x2的图象相同,∴a=-?,∴抛物线的表达式为
15.
答案 -1.5
?∵x=3时,y=2.5;x=5时,y=2.5,∴抛物线的对称轴为直线x=4,∴x=1和x=7的函数值相等,而x=7时,y=-1.5,∴x=1时,y=a+b+c=-1.5.
16.
答案 3
解析????由表中的数据可知抛物线开口向上,顶点为(1,3),与y轴的交点为(0,4),
∴b<0,∴ac>0,
∴函数y=bx+ac的图象经过第一、二、四象限,不经过第三象限,∴m=3.
17.
答案 ②③
解析????①观察图象可知,a>0,b<0,c<0,∴abc>0.∴①错误.②观察图象可知,当x=3时,y=0,即9a+3b+c=0,∵a>0,∴10a+3b+c>0.∴②正确.③∵对称轴为x=1,∴b=-2a,∴am2+bm+a=am2-2am+a=a(m-1)2≥0,
∴am2+bm+a≥0.∴③正确.
18.
答案????y=2x2+8x或y=2x2-8x
函数y=a(x-h)2+k的图象经过原点,把(0,0)代入解析式,得ah2+k=0,∵最小值为-8,∴函数图象的开口向上,a>0,顶点的纵坐标k=-8,又∵形状与抛物线y=-2x2-2x+3相同,∴二次项系数a=2,把a=2,k=-8代入ah2+k=0中,得h=±2,∴函数解析式是y=2(x+2)2-8或y=2(x-2)2-8,即y=2x2+8x或y=2x2-8x.
19.
答案????y=-x2-2x-2
∵抛物线y=-x2+4x-3=-(x-2)2+1,∴顶点坐标为(2,1),将顶点向左平移3个单位,再向下平移2个单位得到的点是(-1,-1),则变换后的抛物线解析式为y=-(x+1)2-1=-x2-2x-2.
20.
解析????(1)∵点A的坐标为(-1,0),点B的坐标为(4,0),∴AB=4-(-1)=5,
∵AB=OC,∴OC=5,∴点C的坐标为(0,5).
(2)解法一:设过点A,B,C的抛物线的解析式为y=ax2+bx+c,
把A(-1,0),B(4,0),C(0,5)分别代入y=ax2+bx+c中,得?
解得?
所以二次函数的解析式为
解法二:设过点A,B的抛物线的解析式为y=a(x+1)(x-4),
把点C(0,5)代入,得5=a(0+1)(0-4),
所以二次函数的解析式为
21.
解??(1)把(0,1),(1,-2),(2,1)代入y=ax2+bx+c中,得?
解得?
所以二次函数解析式为y=3x2-6x+1.
(2)由(1)知抛物线解析式为y=3x2-6x+1,
即y=3(x2-2x)+1=3(x2-2x+1-1)+1=3(x-1)2-2,
所以抛物线的顶点坐标为(1,-2).
初中数学(人教版)九年级
上册
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c第的图象和性质
1.(2020湖北十堰丹江口期中)关于抛物线y=x2-2x-1,下列说法中错误的是?( )
A.开口方向向上
B.对称轴是直线x=1
C.当x>1时,y随x的增大而减小
D.顶点坐标为(1,-2)
2.(2019吉林四平铁西期中)二次函数y=-2x2-3x+1的图象大致是?( )
3.
(2020重庆八中月考)如图,已知抛物线y=ax2+bx+c(a≠0)经过点(-2,0),对称轴为直线x=1,下列结论中正确的是?( )
A.abc>0 ????B.b=2a
C.9a+3b+c<0 ????D.8a+c=0
4.
(2020天津和平期中)抛物线的顶点为(1,-4),与y轴交于点(0,-3),则该抛物线的解析式为?( )
A.y=x2-2x-3 ????B.y=x2+2x-3
C.y=x2-2x+3 ????D.y=2x2-3x-3
5.
(2020浙江嘉兴秀洲期中)二次函数y=ax2+bx+c的图象经过点A(-4,0)、B(-1,0)和C(-2,-2),则下列说法正确的是?( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴是直线x=-
?
6.
(2020天津和平期中)二次函数y=x2+bx+c(b,c是常数)中的自变量x与函数值y的部分对应值如下表:
x
…
-1
0
1
2
3
4
…
y
…
10
5
2
1
2
5
…
下列结论正确的是?( )
A.当x=2时,y有最大值1
B.当x<2时,y随x的增大而增大
C.点(5,9)在该函数的图象上
D.若A(m,y1),B(m+1,y2)两点都在该函数的图象上,则当m>3/2?时,y1
8.
(2019重庆中考)抛物线y=-3x2+6x+2的对称轴是?( )
A.直线x=2 ????B.直线x=-2
C.直线x=1 ????D.直线x=-1
9.
(2019辽宁葫芦岛中考)二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象大致是?( )
10.
(2019四川遂宁中考)二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是?( )
A.a=4
B.当b=-4时,顶点的坐标为(2,-8)
C.当x=-1时,b>-5
D.当x>3时,y随x的增大而增大
11.
(2020独家原创试题)已知A(a,m),B(b,n)是抛物线y=x2-2x-2
020上的两点,且a
C.第二、三、四象限 ????D.第一、三、四象限
12.
(2019江苏徐州铜山二模)二次函数y=x2+2x+2的图象先向上平移2个单位长度,再向右平移3个单位长度,则平移后二次函数图象的顶点坐标是 ????.
13.
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在第 ????象限.
14.
(2020山东青岛莱西期中)顶点为(-6,0),开口向下,形状与函数y=
x2的图象相同的抛物线的表达式是 ????.
15.
(2019北京西城期中)已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中自变量x与函数值y之间满足下面的对应关系:
x
…
3
5
7
…
y
…
2.5
2.5
-1.5
…
则a+b+c= ????.
16.
(2020重庆巴南期中)已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x
0
1
2
y
4
3
4
若一次函数y=bx+ac的图象不经过第m象限,则m= ????
17.
(2020湖北孝感孝南期中)如图,抛物线y=ax2+bx+c的图象经过(-1,0),对称轴为x=1,则下列三个结论:
①abc<0;②10a+3b+c>0;③am2+bm+a≥0,其中正确的结论为 ???? ????(填序号).
18.
(2019福建莆田秀屿月考)若函数y=a(x-h)2+k的图象经过原点,最小值为-8且形状与抛物线y=-2x2-2x+3相同,则此函数关系式为????.
19.
(2020北京三十九中期中)把抛物线y=-x2+4x-3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是 ????.
20.
(2019福建龙岩上杭月考)如图,二次函数图象过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求二次函数的解析式.
21.
(2019山东淄博临淄期中)已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
x
…
-1
0
1
2
4
…
y
…
10
1
-2
1
25
…
(1)求这个二次函数的解析式;
(2)写出这个二次函数图象的顶点坐标.
参考答案
1.
答案????C
∵a=1>0,∴开口方向向上,故A说法正确;对称轴是
故B说法正确;当x>1时,y随x的增大而增大,故C说法错误;y=x2-2x-1=(x-1)2-2,顶点坐标为(1,-2),故D说法正确.故选C.
2.
答案????B
因为a=-2<0,所以抛物线y=-2x2-3x+1开口向下,故C、D不符合题意;抛物线y=-2x2-3x+1的对称轴是直线
故A不符合题意.故选B.
3.
答案????D ∵抛物线开口向下,∴a<0,∵抛物线对称轴为直线x=1,∴-b/2a?=1,∴b=-2a>0,故B错误;∵抛物线与y轴的正半轴相交,∴c>0,∴abc<0,故A错误;∵对称轴为直线x=1,又点(-2,0)关于直线x=1的对称点的坐标为(4,0),∴当x=3时,y=9a+3b+c>0,故C错误;∵抛物线y=ax2+bx+c经过点(-2,0),∴4a-2b+c=0,∵b=-2a,∴4a+4a+c=0,即8a+c=0,故D正确.故选D.
4.
答案????A 设抛物线的解析式为y=a(x-1)2-4,将(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4,解得a=1,∴抛物线的解析式为y=(x-1)2-4=x2-2x-3.故选A.
5.
答案????D ∵二次函数y=ax2+bx+c的图象经过点A(-4,0)、B(-1,0)和C(-2,-2),∴a>0,∴抛物线开口向上,故A错误;对称轴为直线
y随x的增大而增大,故B错误,D正确;
∴函数的最小值小于-2,故C错误.故选D.
6.
答案????D 观察表格知,函数的图象经过点(1,2)和(3,2),∴对称轴为x=2.∵函数图象开口向上且经过点(2,1),∴x=2时,y有最小值1,故A错误.易知当x<2时,y随x的增大而减小,故B错误.∵对称轴是直线x=2,点(-1,10)关于x=2的对称点是(5,10),∴点(5,10)在该函数的图象上,点(5,9)不在该函数的图象上,故C错误.∵当m>3/2?时,|2-m|<|m+1-2|,∴y1
答案????C 在函数y=ax2+ax+a(a≠0)中,当a<0时,该函数图象开口向下,顶点在y轴左侧,抛物线与y轴的负半轴相交,故C正确、D错误;当a>0时,该函数图象开口向上,顶点在y轴左侧,抛物线与y轴的正半轴相交,故A、B错误.故选C.
8.
答案????C
9.
答案????D
10.
答案????C 由题意得,对称轴为直线x=2,∴a=4,故A正确;当b=-4时,y=x2-4x-4=(x-2)2-8,∴顶点的坐标为(2,-8),故B正确;当x=-1时,由图象知此时y<0,即1+4+b<0,∴b<-5,故C不正确;∵对称轴为直线x=2且图象开口向上,∴当x>3时,y随x的增大而增大,故D正确.故选C.
11.
答案????B????y=x2-2x-2
020=(x-1)2-2
021,∴抛物线开口向上,对称轴为x=1,当x<1时,y随x的增大而减小.∵A(a,m),B(b,n)是抛物线y=x2-2x-2
020上的两点,且a
12.
答案 (2,3)
∵y=x2+2x+2=(x+1)2+1,顶点为(-1,1),
∴将图象向上平移2个单位长度,
再向右平移3个单位长度,平移后的二次函数图象的顶点坐标为(2,3).
13.
答案 一
14.
解析????设所求的抛物线的表达式为y=a(x-h)2+k,∵顶点为(-6,0),∴h=-6,k=0,又∵开口向下,形状与函数y=?x2的图象相同,∴a=-?,∴抛物线的表达式为
15.
答案 -1.5
?∵x=3时,y=2.5;x=5时,y=2.5,∴抛物线的对称轴为直线x=4,∴x=1和x=7的函数值相等,而x=7时,y=-1.5,∴x=1时,y=a+b+c=-1.5.
16.
答案 3
解析????由表中的数据可知抛物线开口向上,顶点为(1,3),与y轴的交点为(0,4),
∴b<0,∴ac>0,
∴函数y=bx+ac的图象经过第一、二、四象限,不经过第三象限,∴m=3.
17.
答案 ②③
解析????①观察图象可知,a>0,b<0,c<0,∴abc>0.∴①错误.②观察图象可知,当x=3时,y=0,即9a+3b+c=0,∵a>0,∴10a+3b+c>0.∴②正确.③∵对称轴为x=1,∴b=-2a,∴am2+bm+a=am2-2am+a=a(m-1)2≥0,
∴am2+bm+a≥0.∴③正确.
18.
答案????y=2x2+8x或y=2x2-8x
函数y=a(x-h)2+k的图象经过原点,把(0,0)代入解析式,得ah2+k=0,∵最小值为-8,∴函数图象的开口向上,a>0,顶点的纵坐标k=-8,又∵形状与抛物线y=-2x2-2x+3相同,∴二次项系数a=2,把a=2,k=-8代入ah2+k=0中,得h=±2,∴函数解析式是y=2(x+2)2-8或y=2(x-2)2-8,即y=2x2+8x或y=2x2-8x.
19.
答案????y=-x2-2x-2
∵抛物线y=-x2+4x-3=-(x-2)2+1,∴顶点坐标为(2,1),将顶点向左平移3个单位,再向下平移2个单位得到的点是(-1,-1),则变换后的抛物线解析式为y=-(x+1)2-1=-x2-2x-2.
20.
解析????(1)∵点A的坐标为(-1,0),点B的坐标为(4,0),∴AB=4-(-1)=5,
∵AB=OC,∴OC=5,∴点C的坐标为(0,5).
(2)解法一:设过点A,B,C的抛物线的解析式为y=ax2+bx+c,
把A(-1,0),B(4,0),C(0,5)分别代入y=ax2+bx+c中,得?
解得?
所以二次函数的解析式为
解法二:设过点A,B的抛物线的解析式为y=a(x+1)(x-4),
把点C(0,5)代入,得5=a(0+1)(0-4),
所以二次函数的解析式为
21.
解??(1)把(0,1),(1,-2),(2,1)代入y=ax2+bx+c中,得?
解得?
所以二次函数解析式为y=3x2-6x+1.
(2)由(1)知抛物线解析式为y=3x2-6x+1,
即y=3(x2-2x)+1=3(x2-2x+1-1)+1=3(x-1)2-2,
所以抛物线的顶点坐标为(1,-2).
同课章节目录
