人教版初中数学九年级上册22.2二次函数与一元二次方程课后提升训练试卷(含解析)
文档属性
| 名称 | 人教版初中数学九年级上册22.2二次函数与一元二次方程课后提升训练试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览


文档简介
2020年秋绵阳南山双语学校
初中数学(人教版)九年级
上册
第二十二章 二次函数
22.2 二次函数与一元二次方程
1.(2019北京通州期中)在平面直角坐标系xOy中,二次函数y=x2-4x的图象与x轴的交点坐标是?( )
A.(0,0) ????B.(4,0)
C.(4,0)、(0,0) ???D.(2,0)、(-2,0)
2.(2020吉林长春南关月考)若抛物线y=x2-6x+m与x轴只有一个交点,则m的值为?( )
A.-6 ????B.6 ????
C.3 ????D.9
3.(2020浙江绍兴诸暨期中)抛物线y=x2-6x+9与坐标轴的交点个数是?( )
A.0 ????B.1 ????
C.2 ????D.3
4.
(2019浙江湖州南浔期末)二次函数y=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
y
-12
-5
0
3
4
3
利用二次函数的图象可知,当函数值y>0时,x的取值范围是?( )
A.02
C.-13
5.
(2020河南洛阳期中)已知二次函数y=x2+bx+c的部分图象如图所示,若-1A.-3≤y<0 ????B.-4≤x<-3
C.-46.
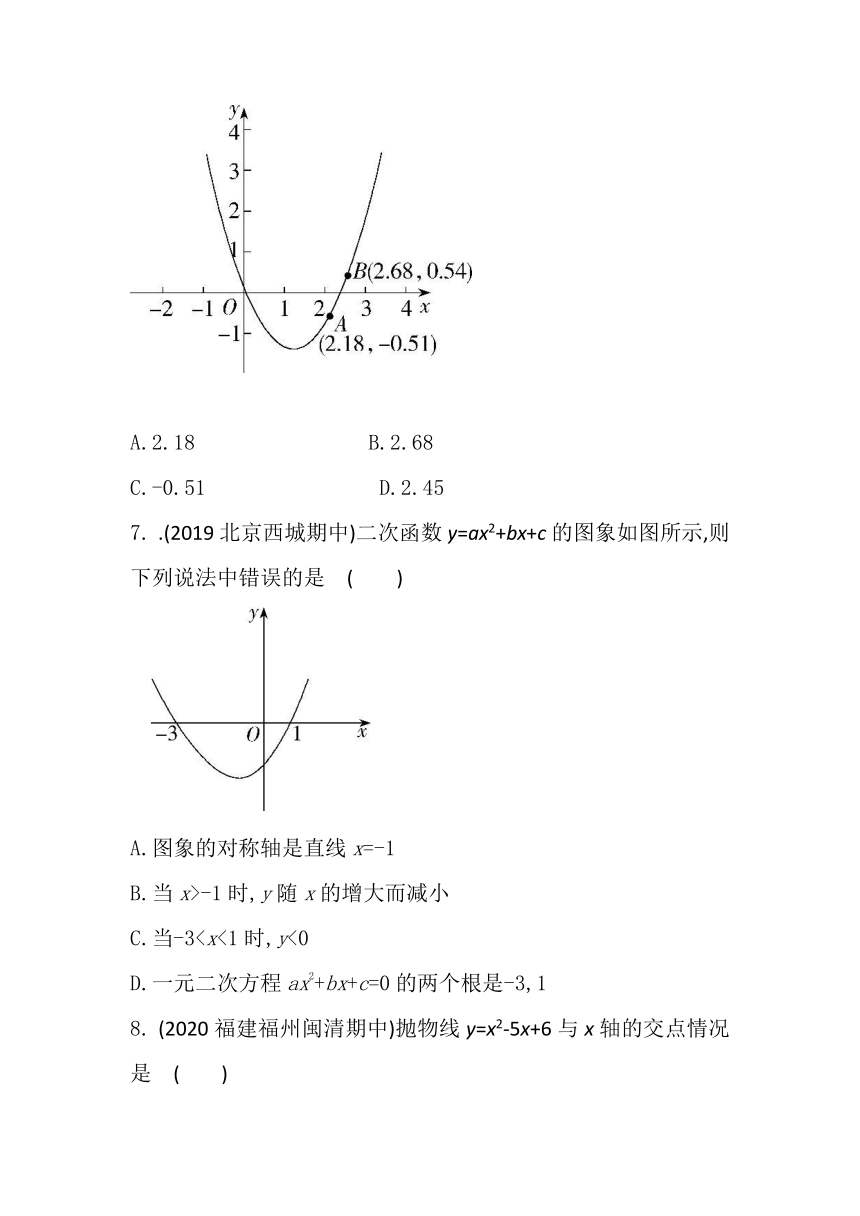
(2019福建漳州期中)如图,点A(2.18,-0.51)和B(2.68,0.54)在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似值可能是?( )
A.2.18 ????B.2.68 ????
C.-0.51 ????D.2.45
7.
.(2019北京西城期中)二次函数y=ax2+bx+c的图象如图所示,则下列说法中错误的是?( )
?
A.图象的对称轴是直线x=-1
B.当x>-1时,y随x的增大而减小
C.当-3D.一元二次方程ax2+bx+c=0的两个根是-3,1
8.
(2020福建福州闽清期中)抛物线y=x2-5x+6与x轴的交点情况是?(???? )
A.有两个交点 ????B.只有一个交点
C.没有交点 ????D.无法判断
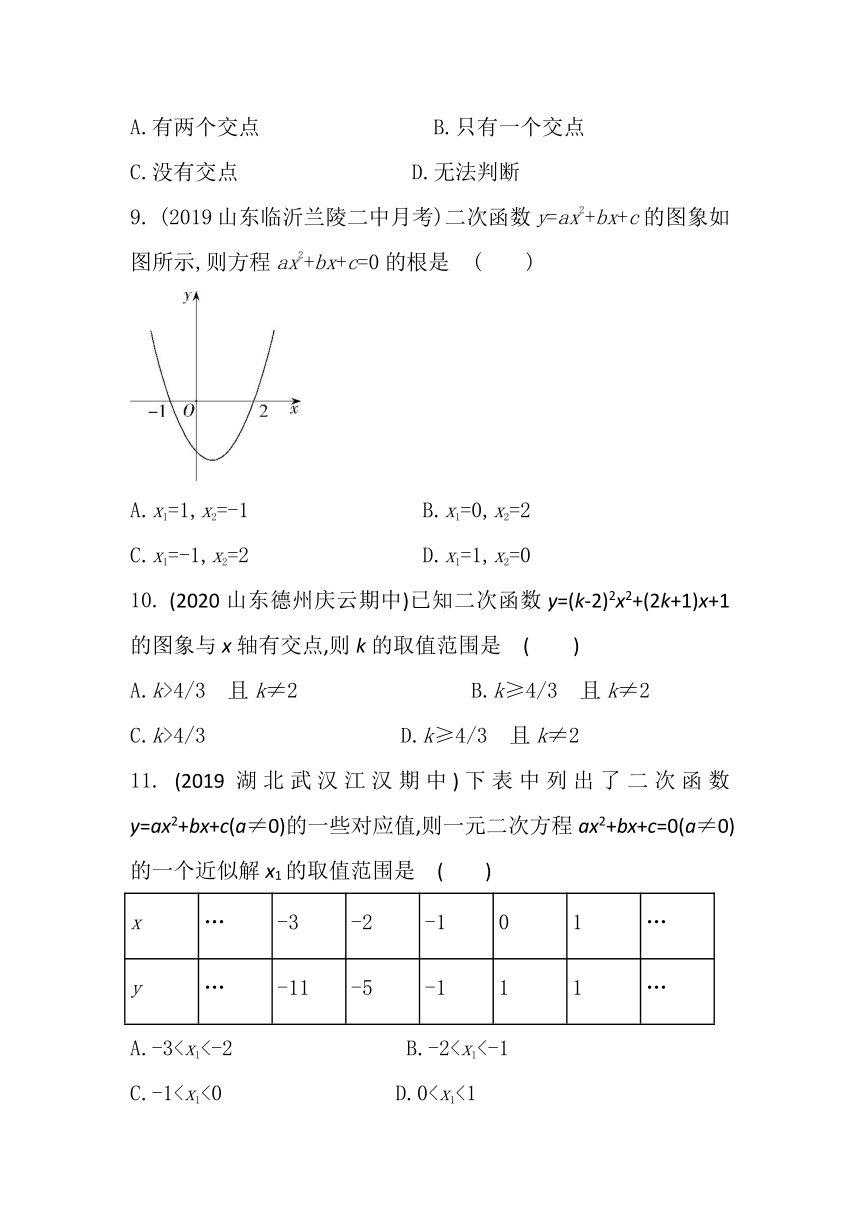
9.
(2019山东临沂兰陵二中月考)二次函数y=ax2+bx+c的图象如图所示,则方程ax2+bx+c=0的根是?( )
A.x1=1,x2=-1 ????B.x1=0,x2=2
C.x1=-1,x2=2 ????D.x1=1,x2=0
10.
(2020山东德州庆云期中)已知二次函数y=(k-2)2x2+(2k+1)x+1的图象与x轴有交点,则k的取值范围是?( )
A.k>4/3?且k≠2 ????B.k≥4/3?且k≠2
C.k>4/3? ????D.k≥4/3?且k≠2
11.
(2019湖北武汉江汉期中)下表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的取值范围是?(???? )
x
…
-3
-2
-1
0
1
…
y
…
-11
-5
-1
1
1
…
A.-3C.-112.
(2019四川达州渠县月考)二次函数y=x2-6x-7的图象与x轴的交点坐标是 ???? ????,与y轴的交点坐标是 ????.
13.
(2019广西梧州蒙山二中月考)已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(5,0),则一元二次方程ax2+bx+c=0(a≠0)的根是 ????.
14.
(2020江苏徐州睢宁期中)二次函数y=2(x-1)(x+5)的图象与x轴的两个交点之间的距离是 ????.
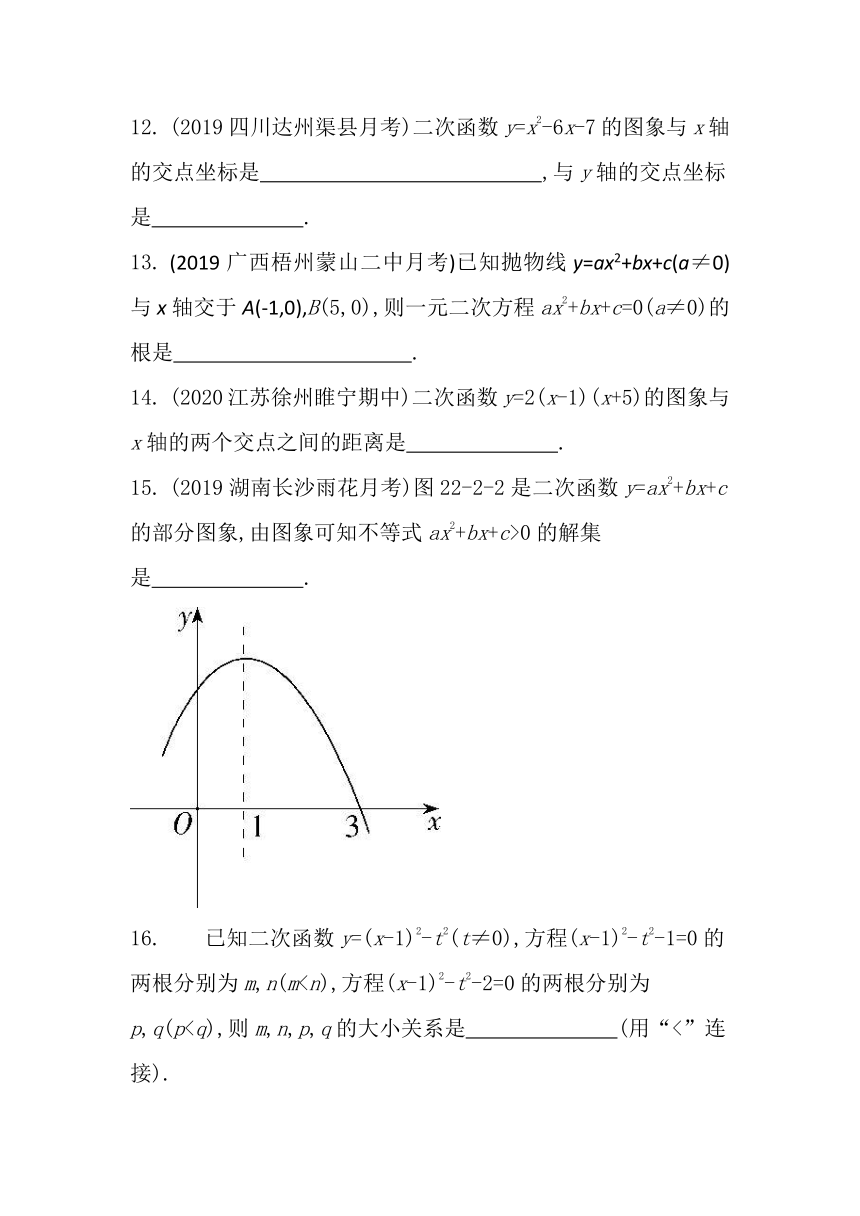
15.
(2019湖南长沙雨花月考)图22-2-2是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是 ????.
16.
已知二次函数y=(x-1)2-t2(t≠0),方程(x-1)2-t2-1=0的两根分别为m,n(m17.
(2019湖南长沙雨花二模)如图,抛物线y=ax2+bx+c的对称轴是x=-1,与x轴的一个交点为(-5,0),则不等式ax2+bx+c>0的解集为 ????.
18.
(2018四川自贡中考)若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为 ????.
19.
(2020独家原创试题)如图,有一段抛物线C1:y=-x2+4x(0≤x≤4),它与x轴交于两点O,A;将C1沿x轴向右平移OA的长度得到C2,与x轴的另一个交点为A1;按照上面的操作,得到C3,C4,…,与x轴的另一个交点分别是A2,A3,…,如此进行下去,直至得到C2
020,若点P(m,3)在第2
020段抛物线上,则m的值为 ????.
?
20.
已知抛物线y=2(k+1)x2+4kx+2k-3,求:
(1)k为何值时,抛物线与x轴有两个交点;
(2)k为何值时,抛物线与x轴有唯一交点;
(3)k为何值时,抛物线与x轴没有交点.
21.
(2020安徽合肥包河月考)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(-1,-3),与x轴交于A(-3,0),B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小时自变量x的取值范围;
(4)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
22.
(2019云南中考)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
23.
(2019山东威海中考)在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
x
…
-1
0
1
2
3
…
y甲
…
6
3
2
3
6
…
乙写错了常数项,列表如下:
x
…
-1
0
1
2
3
…
y乙
…
-2
-1
2
7
14
…
通过上述信息,解决以下问题:
求原二次函数y=ax2+bx+c(a≠0)的表达式
(2)对于二次函数y=ax2+bx+c(a≠0),当x ????时,y的值随x的值增大而增大;
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
参考答案
1.
答案????C 令y=0,得x2-4x=0,即x(x-4)=0,解得x=0或x=4,∴二次函数y=x2-4x的图象与x轴的交点坐标是(0,0)、(4,0),故选C.
2.
答案????D????根据题意得Δ=(-6)2-4m=0,解得m=9.故选D
3.
答案????C ∵b2-4ac=(-6)2-4×1×9=0,∴二次函数y=x2-6x+9的图象与x轴有1个交点.∵抛物线y=x2-6x+9与y轴有1个交点,∴抛物线y=x2-6x+9与坐标轴的交点的个数是2.故选C.
4.
答案????C 从表格可以看出,二次函数的图象的对称轴为直线x=1,故当x=-1或3时,y=0,∴当-10.故选C.
5.
答案????D ∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),结合题意知抛物线的解析式为y=(x+1)(x-3).∵y=(x+1)(x-3)=(x-1)2-4,∴x=1时,y有最小值-4.∵x=2时,y=(x+1)(x-3)=-3,
∴当-16.
答案????D ∵图象上有两点,分别为A(2.18,-0.51),B(2.68,0.54),∴当x=2.18时,y=-0.51<0;当x=2.68时,y=0.54>0,∴在2.18与2.68之间,必存在一个x值使y=0(此时对应二次函数图象与x轴的一个交点),又∵2.18<2.45<2.68,故选项D符合.由图象可知,二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点在0和1之间,无选项符合.故选D.
7.
答案????B 因为抛物线与x轴的交点坐标为(-3,0),(1,0),所以抛物线的对称轴为直线x=-1,所以A选项的说法正确;因为对称轴为x=-1,且抛物线开口向上,所以当x>-1时,y随x的增大而增大,所以B选项的说法错误;由题图知当-38.
答案????A 解法一:∵y=x2-5x+6=(x-2)(x-3),∴当y=0时,x=2或x=3,即抛物线y=x2-5x+6与x轴的交点坐标为(2,0),(3,0),故抛物线y=x2-5x+6与x轴有两个交点.故选A.
解法二:∵Δ=(-5)2-4×1×6=1>0,∴抛物线与x轴有两个交点.故选A.
9.
答案????C????由题图得抛物线与x轴的交点坐标为(-1,0),(2,0),所以方程ax2+bx+c=0的根为x1=-1,x2=2.故选C.
10.
答案????D 根据题意得k-2≠0且Δ=(2k+1)2-4(k-2)2≥0,解得k≥4/3?且k≠2.故选D.
11.
答案????C 当x=-1时,y=-1,x=0时,y=1,同时在-3≤x≤0范围内,y随x的增大而增大,∴方程ax2+bx+c=0(a≠0)的一个近似解x1的取值范围为-112.
答案 (7,0),(-1,0);(0,-7)
当y=0时,0=x2-6x-7,解得x1=7,x2=-1,∴二次函数y=x2-6x-7的图象与x轴的交点坐标是(7,0),(-1,0).当x=0时,y=-7,∴二次函数y=x2-6x-7的图象与y轴的交点坐标是(0,-7).
13.
答案????x1=-1,x2=5
?∵抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(5,0),∴方程ax2+bx+c=0(a≠0)的两根为x1=-1,x2=5.
14.
答案??6
当y=0时,2(x-1)(x+5)=0,解得x1=1,x2=-5,∴二次函数y=2(x-1)(x+5)的图象与x轴的交点坐标是(1,0),(-5,0),∴两个交点之间的距离是1-(-5)=6.
15.
答案 -1∵抛物线的对称轴为直线x=1,而抛物线与x轴的一个交点坐标为(3,0),∴抛物线与x轴的另一个交点坐标为(-1,0),∴当-10.
16.
答案????p二次函数y=(x-1)2-t2(t≠0)的图象如图:
?
根据图象易知p17.
答案 -5抛物线的对称轴是x=-1,与x轴的一个交点坐标为(-5,0),∴抛物线与x轴的另一个交点的坐标为(3,0),由图象可知,当-50的解集是-518.
答案 -1
∵函数y=x2+2x-m的图象与x轴有且只有一个交点,
∴Δ=22-4×1×(-m)=0,解得m=-1.
19.
答案 8
077或8
079
当y=0时,-x2+4x=0,解得x1=0,x2=4,则A(4,0),∴OA=4,∴抛物线C2
020与x轴的两个交点到原点的距离分别为2
019×4=8
076,2
020×4=8
080.把y=3代入y=-x2+4x得-x2+4x=3,解得x=1或x=3.把C1上的纵坐标为3的点按照抛物线平移的规律进行平移就得到第2
020段抛物线上的点P(m,3),∴m=8
076+1=8
077或m=8
080-1=8
079,即m=8
077或m=8
079.
20.
解
??Δ=(4k)2-4×2(k+1)(2k-3)=16k2-8(2k2-k-3)=8k+24.
(1)当8k+24>0,且2(k+1)≠0,即k>-3且k≠-1时,抛物线与x轴有两个交点.
(2)当8k+24=0,且2(k+1)≠0,即k=-3时,抛物线与x轴有唯一交点.
(3)当8k+24<0,且2(k+1)≠0,即k<-3时,抛物线与x轴没有交点.
21.
解????(1)∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0),B(1,0),
∴ax2+bx+c=0的根为x1=-3,x2=1.
(2)观察图象可知,当x<-3或x>1时,图象总在x轴的上方,∴不等式ax2+bx+c>0的解集为x<-3或x>1.
(3)由题意知,该图象的对称轴为直线x=-1,
又∵图象开口向上,
∴当x<-1时,y随x的增大而减小,
即y随x的增大而减小时x<-1.
(4)∵方程ax2+bx+c=k有实数根,∴抛物线y=ax2+bx+c与直线y=k有交点,由函数图象知k≥-3.
22.
解??(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,
∴k2+k-6=0,解得k1=-3,k2=2.
又∵抛物线y=x2+(k2+k-6)x+3k与x轴有两个交点,
∴Δ=02-4×3k>0(或3k<0),∴k<0,∴k=-3.
此时抛物线的关系式为y=x2-9.
(2)∵点P在抛物线y=x2-9上,且P到y轴的距离是2,
∴点P的横坐标为2或-2,
当x=2时,y=-5,当x=-2时,y=-5.
∴P(2,-5)或P(-2,-5),
因此点P的坐标为(2,-5)或(-2,-5)
23.
解????
(1)根据甲同学提供的数据,把x=0,y=3;x=-1,y=6;x=1,y=2代入二次函数解析式可得?
解得?
根据乙同学提供的数据,把x=0,y=-1;x=-1,y=-2;x=1,y=2代入二次函数解析式可得
?解得?
根据题意得,y=x2+2x+3.
初中数学(人教版)九年级
上册
第二十二章 二次函数
22.2 二次函数与一元二次方程
1.(2019北京通州期中)在平面直角坐标系xOy中,二次函数y=x2-4x的图象与x轴的交点坐标是?( )
A.(0,0) ????B.(4,0)
C.(4,0)、(0,0) ???D.(2,0)、(-2,0)
2.(2020吉林长春南关月考)若抛物线y=x2-6x+m与x轴只有一个交点,则m的值为?( )
A.-6 ????B.6 ????
C.3 ????D.9
3.(2020浙江绍兴诸暨期中)抛物线y=x2-6x+9与坐标轴的交点个数是?( )
A.0 ????B.1 ????
C.2 ????D.3
4.
(2019浙江湖州南浔期末)二次函数y=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
y
-12
-5
0
3
4
3
利用二次函数的图象可知,当函数值y>0时,x的取值范围是?( )
A.0
C.-1
5.
(2020河南洛阳期中)已知二次函数y=x2+bx+c的部分图象如图所示,若-1
C.-4
(2019福建漳州期中)如图,点A(2.18,-0.51)和B(2.68,0.54)在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似值可能是?( )
A.2.18 ????B.2.68 ????
C.-0.51 ????D.2.45
7.
.(2019北京西城期中)二次函数y=ax2+bx+c的图象如图所示,则下列说法中错误的是?( )
?
A.图象的对称轴是直线x=-1
B.当x>-1时,y随x的增大而减小
C.当-3
8.
(2020福建福州闽清期中)抛物线y=x2-5x+6与x轴的交点情况是?(???? )
A.有两个交点 ????B.只有一个交点
C.没有交点 ????D.无法判断
9.
(2019山东临沂兰陵二中月考)二次函数y=ax2+bx+c的图象如图所示,则方程ax2+bx+c=0的根是?( )
A.x1=1,x2=-1 ????B.x1=0,x2=2
C.x1=-1,x2=2 ????D.x1=1,x2=0
10.
(2020山东德州庆云期中)已知二次函数y=(k-2)2x2+(2k+1)x+1的图象与x轴有交点,则k的取值范围是?( )
A.k>4/3?且k≠2 ????B.k≥4/3?且k≠2
C.k>4/3? ????D.k≥4/3?且k≠2
11.
(2019湖北武汉江汉期中)下表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的取值范围是?(???? )
x
…
-3
-2
-1
0
1
…
y
…
-11
-5
-1
1
1
…
A.-3
(2019四川达州渠县月考)二次函数y=x2-6x-7的图象与x轴的交点坐标是 ???? ????,与y轴的交点坐标是 ????.
13.
(2019广西梧州蒙山二中月考)已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(5,0),则一元二次方程ax2+bx+c=0(a≠0)的根是 ????.
14.
(2020江苏徐州睢宁期中)二次函数y=2(x-1)(x+5)的图象与x轴的两个交点之间的距离是 ????.
15.
(2019湖南长沙雨花月考)图22-2-2是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是 ????.
16.
已知二次函数y=(x-1)2-t2(t≠0),方程(x-1)2-t2-1=0的两根分别为m,n(m
(2019湖南长沙雨花二模)如图,抛物线y=ax2+bx+c的对称轴是x=-1,与x轴的一个交点为(-5,0),则不等式ax2+bx+c>0的解集为 ????.
18.
(2018四川自贡中考)若函数y=x2+2x-m的图象与x轴有且只有一个交点,则m的值为 ????.
19.
(2020独家原创试题)如图,有一段抛物线C1:y=-x2+4x(0≤x≤4),它与x轴交于两点O,A;将C1沿x轴向右平移OA的长度得到C2,与x轴的另一个交点为A1;按照上面的操作,得到C3,C4,…,与x轴的另一个交点分别是A2,A3,…,如此进行下去,直至得到C2
020,若点P(m,3)在第2
020段抛物线上,则m的值为 ????.
?
20.
已知抛物线y=2(k+1)x2+4kx+2k-3,求:
(1)k为何值时,抛物线与x轴有两个交点;
(2)k为何值时,抛物线与x轴有唯一交点;
(3)k为何值时,抛物线与x轴没有交点.
21.
(2020安徽合肥包河月考)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(-1,-3),与x轴交于A(-3,0),B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小时自变量x的取值范围;
(4)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
22.
(2019云南中考)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
23.
(2019山东威海中考)在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下:
x
…
-1
0
1
2
3
…
y甲
…
6
3
2
3
6
…
乙写错了常数项,列表如下:
x
…
-1
0
1
2
3
…
y乙
…
-2
-1
2
7
14
…
通过上述信息,解决以下问题:
求原二次函数y=ax2+bx+c(a≠0)的表达式
(2)对于二次函数y=ax2+bx+c(a≠0),当x ????时,y的值随x的值增大而增大;
(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根,求k的取值范围.
参考答案
1.
答案????C 令y=0,得x2-4x=0,即x(x-4)=0,解得x=0或x=4,∴二次函数y=x2-4x的图象与x轴的交点坐标是(0,0)、(4,0),故选C.
2.
答案????D????根据题意得Δ=(-6)2-4m=0,解得m=9.故选D
3.
答案????C ∵b2-4ac=(-6)2-4×1×9=0,∴二次函数y=x2-6x+9的图象与x轴有1个交点.∵抛物线y=x2-6x+9与y轴有1个交点,∴抛物线y=x2-6x+9与坐标轴的交点的个数是2.故选C.
4.
答案????C 从表格可以看出,二次函数的图象的对称轴为直线x=1,故当x=-1或3时,y=0,∴当-1
5.
答案????D ∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),结合题意知抛物线的解析式为y=(x+1)(x-3).∵y=(x+1)(x-3)=(x-1)2-4,∴x=1时,y有最小值-4.∵x=2时,y=(x+1)(x-3)=-3,
∴当-1
答案????D ∵图象上有两点,分别为A(2.18,-0.51),B(2.68,0.54),∴当x=2.18时,y=-0.51<0;当x=2.68时,y=0.54>0,∴在2.18与2.68之间,必存在一个x值使y=0(此时对应二次函数图象与x轴的一个交点),又∵2.18<2.45<2.68,故选项D符合.由图象可知,二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点在0和1之间,无选项符合.故选D.
7.
答案????B 因为抛物线与x轴的交点坐标为(-3,0),(1,0),所以抛物线的对称轴为直线x=-1,所以A选项的说法正确;因为对称轴为x=-1,且抛物线开口向上,所以当x>-1时,y随x的增大而增大,所以B选项的说法错误;由题图知当-3
答案????A 解法一:∵y=x2-5x+6=(x-2)(x-3),∴当y=0时,x=2或x=3,即抛物线y=x2-5x+6与x轴的交点坐标为(2,0),(3,0),故抛物线y=x2-5x+6与x轴有两个交点.故选A.
解法二:∵Δ=(-5)2-4×1×6=1>0,∴抛物线与x轴有两个交点.故选A.
9.
答案????C????由题图得抛物线与x轴的交点坐标为(-1,0),(2,0),所以方程ax2+bx+c=0的根为x1=-1,x2=2.故选C.
10.
答案????D 根据题意得k-2≠0且Δ=(2k+1)2-4(k-2)2≥0,解得k≥4/3?且k≠2.故选D.
11.
答案????C 当x=-1时,y=-1,x=0时,y=1,同时在-3≤x≤0范围内,y随x的增大而增大,∴方程ax2+bx+c=0(a≠0)的一个近似解x1的取值范围为-1
答案 (7,0),(-1,0);(0,-7)
当y=0时,0=x2-6x-7,解得x1=7,x2=-1,∴二次函数y=x2-6x-7的图象与x轴的交点坐标是(7,0),(-1,0).当x=0时,y=-7,∴二次函数y=x2-6x-7的图象与y轴的交点坐标是(0,-7).
13.
答案????x1=-1,x2=5
?∵抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(5,0),∴方程ax2+bx+c=0(a≠0)的两根为x1=-1,x2=5.
14.
答案??6
当y=0时,2(x-1)(x+5)=0,解得x1=1,x2=-5,∴二次函数y=2(x-1)(x+5)的图象与x轴的交点坐标是(1,0),(-5,0),∴两个交点之间的距离是1-(-5)=6.
15.
答案 -1
16.
答案????p
?
根据图象易知p
答案 -5
答案 -1
∵函数y=x2+2x-m的图象与x轴有且只有一个交点,
∴Δ=22-4×1×(-m)=0,解得m=-1.
19.
答案 8
077或8
079
当y=0时,-x2+4x=0,解得x1=0,x2=4,则A(4,0),∴OA=4,∴抛物线C2
020与x轴的两个交点到原点的距离分别为2
019×4=8
076,2
020×4=8
080.把y=3代入y=-x2+4x得-x2+4x=3,解得x=1或x=3.把C1上的纵坐标为3的点按照抛物线平移的规律进行平移就得到第2
020段抛物线上的点P(m,3),∴m=8
076+1=8
077或m=8
080-1=8
079,即m=8
077或m=8
079.
20.
解
??Δ=(4k)2-4×2(k+1)(2k-3)=16k2-8(2k2-k-3)=8k+24.
(1)当8k+24>0,且2(k+1)≠0,即k>-3且k≠-1时,抛物线与x轴有两个交点.
(2)当8k+24=0,且2(k+1)≠0,即k=-3时,抛物线与x轴有唯一交点.
(3)当8k+24<0,且2(k+1)≠0,即k<-3时,抛物线与x轴没有交点.
21.
解????(1)∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0),B(1,0),
∴ax2+bx+c=0的根为x1=-3,x2=1.
(2)观察图象可知,当x<-3或x>1时,图象总在x轴的上方,∴不等式ax2+bx+c>0的解集为x<-3或x>1.
(3)由题意知,该图象的对称轴为直线x=-1,
又∵图象开口向上,
∴当x<-1时,y随x的增大而减小,
即y随x的增大而减小时x<-1.
(4)∵方程ax2+bx+c=k有实数根,∴抛物线y=ax2+bx+c与直线y=k有交点,由函数图象知k≥-3.
22.
解??(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,
∴k2+k-6=0,解得k1=-3,k2=2.
又∵抛物线y=x2+(k2+k-6)x+3k与x轴有两个交点,
∴Δ=02-4×3k>0(或3k<0),∴k<0,∴k=-3.
此时抛物线的关系式为y=x2-9.
(2)∵点P在抛物线y=x2-9上,且P到y轴的距离是2,
∴点P的横坐标为2或-2,
当x=2时,y=-5,当x=-2时,y=-5.
∴P(2,-5)或P(-2,-5),
因此点P的坐标为(2,-5)或(-2,-5)
23.
解????
(1)根据甲同学提供的数据,把x=0,y=3;x=-1,y=6;x=1,y=2代入二次函数解析式可得?
解得?
根据乙同学提供的数据,把x=0,y=-1;x=-1,y=-2;x=1,y=2代入二次函数解析式可得
?解得?
根据题意得,y=x2+2x+3.
同课章节目录
