人教版九年级上册 数学 23.2.1 中心对称 教案
文档属性
| 名称 | 人教版九年级上册 数学 23.2.1 中心对称 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 79.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 20:17:52 | ||
图片预览



文档简介
23.2.1中心对称教学设计
一、教学内容:?
新人教版九年级数学上册第二十三章第二节中心对称第1课时
二、学情分析:?
1、学生是乡镇普通初中九年级的学生,班级学生学习方面存在一定的差异;但学生对数学抱有浓厚的兴趣。?
2、学生在前面已学习了图形的旋转变换,基本上掌握了旋转变换的性质;运用知识解决实际问题的能力和数学建模的能力还不强。?
3、对中心对称概念不易理解;归纳和运用性质也存在困难。?
三、教材分析:?
1、本节课选自人教社九年级数学上册23.2.1中心对称。?
2、中心对称是在学生已掌握旋转变换的基础上,由一般到特殊的方法归纳引出中心对称是特殊的旋转变换。在探索中心对称的概念、性质及应用上,让学生经历动手操作、观察、猜想、归纳等方法,进一步培养学生的自主学习能力以及合作、探究的精神,并在这个过程中增加一定的审美体验。?
3、中心对称承接平移、轴对称等知识,同时是下节学习中心对称图形的基础,又是后续学习几何的桥梁纽带。??
四、教学目标:?
(一)、知识技能:?
1、通过62页思考中图形旋转的演示理解中心对称、对称中心、关于中心的对称点的概念。?
2、结合探究掌握中心对称的性质,会依据中心对称的性质画出与已知图形成中心对称的图形。?
(二)、过程与方法:?
1、通过思考的观察培养学生的观察能力,经历探究性质的过程使学生获得基本的数学活动经验。?
2、通过画出与已知图形成中心对称的图形,进一步培养学生的尺规作图能力。?
(三)、情感、态度与价值观:?
让学生经历观察、操作等过程,理解中心对称的概念,从中心对称基本性质的探索活动,进一步发展学生空间观察能力.让学生通过独立思考,自主探究和合作交流,进一步体会中心对称的数学内涵,获得知识,体验成功。?
五、教学重点:?
中心对称的概念与性质及应用。
六、教学难点:?
中心对称的概念的导入与性质的探究。?
七、教学过程:?
教师引语,创设情境:?
我们生活在多姿多彩的图形世界中,小时候我们就对多姿多彩的图形充满兴趣与好奇,尤其是对运动变换的图形越加的好奇,我邻居家的乐乐对图形也充满着浓厚的兴趣,他画了一幅中心对称的图形,但是不小心被顽皮的弟弟用橡皮擦去了一部分,现在只剩下了这样的图形,于是他跪求!!!帮忙把他画的图形修复,我想让你们帮帮他。今天我们就带着帮助乐乐的爱心走进今天的数学课堂,23.2.1中心对称,学完本节课你将对图形的变换有一个全面深入的了解,也可以帮助乐乐修复他的图形了。下面让我们走进图形世界,走进中心对称。
我们这节课的学习目标
1.理解中心对称的定义.
2.探究中心对称的性质,感受中心对称美.
3.掌握中心对称的性质并利用中心对称的性质作图.
活动一:复习引入
观察图形变换。多媒体演示:旋转。?
幻灯片1是图形变换旋转,那么什么是图形的旋转?图形的旋转有哪些性质呢?学生根据幻灯片的演示回答这些问题。
1、图形的旋转定义:在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换叫做图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角。
2、图形的旋转有哪些性质?
(1)、旋转前后的图形全等;?
????(2)、对应点到旋转中心的距离相等;??
(3)、对应点与旋转中心所连线段的夹角等于旋转角。
生活中有没有旋转角是180度的旋转图形呢?本节课我们就来探究旋转角是180度的旋转图形。?
活动二:创设情景,探索新知.
1.问题:观察实例,回答问题:
①把其中一个图案绕点O旋转180°,你有什么发现?
②线段AC与BD相交于点O,OA=OC,OB=OD,把△AOB绕点O旋转
180?,你有什么发现?
2.引导学生归纳出中心对称的定义:把一个图形绕
旋转
,如果它能够
,那么就说这两个图形
或
;点O叫做
;这两个图形中的对应点叫做关于中心的
.如问题②中的点
与点
、点
与点
、点
与点
。
中心对称的定义要点:(两个图形,一个中心,旋转180度,重合?)
活动三、动手操作,理解性质.
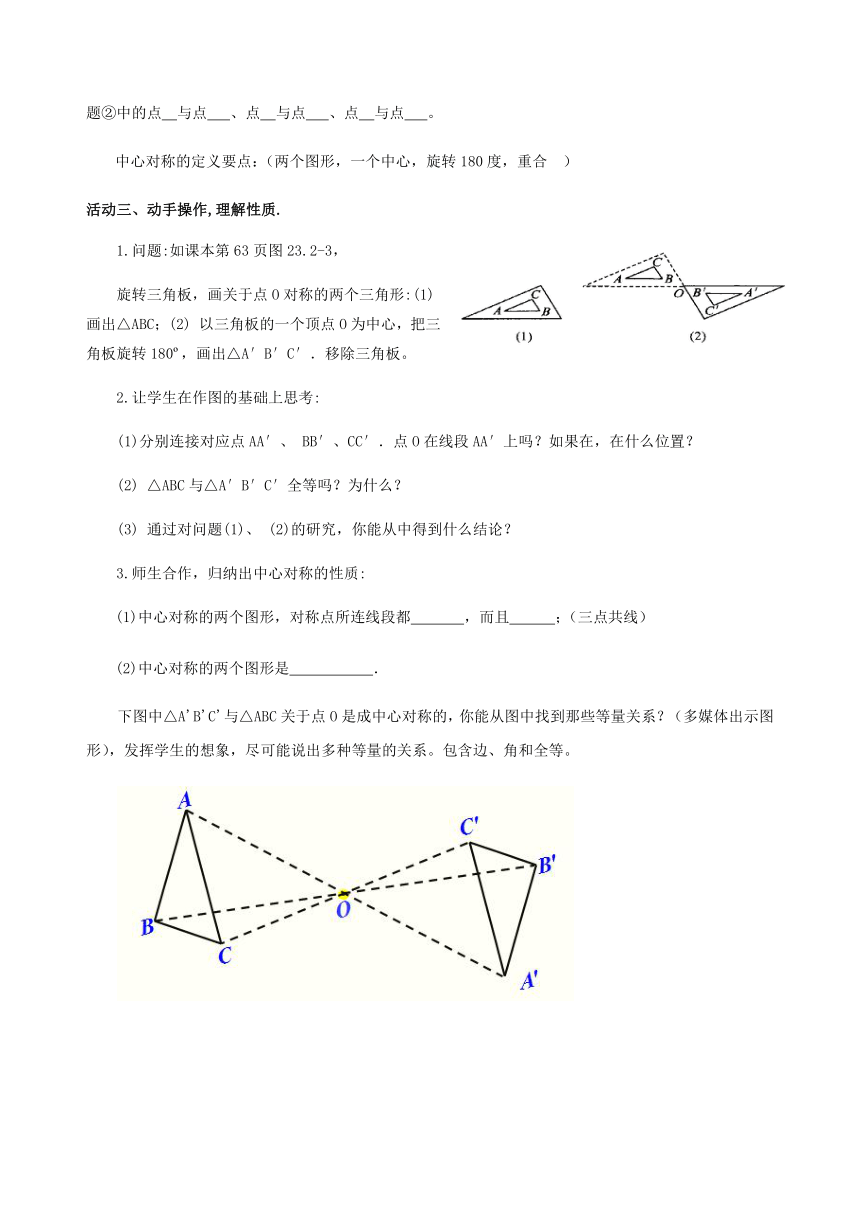
1.问题:如课本第63页图23.2-3,
旋转三角板,画关于点O对称的两个三角形:(1)
画出△ABC;(2)
以三角板的一个顶点O为中心,把三角板旋转180?,画出△A′B′C′.移除三角板。
2.让学生在作图的基础上思考:
(1)分别连接对应点AA′、
BB′、CC′.点O在线段AA′上吗?如果在,在什么位置?
(2)
△ABC与△A′B′C′全等吗?为什么?
(3)
通过对问题(1)、
(2)的研究,你能从中得到什么结论?
3.师生合作,归纳出中心对称的性质:
(1)中心对称的两个图形,对称点所连线段都
,而且
;(三点共线)
(2)中心对称的两个图形是
.
下图中△A'B'C'与△ABC关于点O是成中心对称的,你能从图中找到那些等量关系?(多媒体出示图形),发挥学生的想象,尽可能说出多种等量的关系。包含边、角和全等。
活动四、知识应用,学生动手操作。
1、例题:
如图,选择点O为对称中心,画出点A关于点O的对称点A′;
A.
O.
2、如图,选择点O为对称中心,画出线段AB关于点O的对称线段A′B′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
(分析)
(1)假设点A的对称点A′已经作出,那么连接
A
A′,则这条线段一定经过点
,且
=
。你找到作图方法了吗
?
(2)确定一条线段需要几个点?作一条线段关于某点成中心对称的线段,需要作几个点的
对称点呢?
(3)确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
例2.如图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如多媒体演示)
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如多媒体演示).
活动五、知识运用,中考链接
1.下所英文单词中,是中心对称的有
(
)
A.CEO
B.MBA
C.SOS
D.SAR
如图,已知△AOB与△DOC成中心对称,△AOB的面积
是6,
AB=3,则△DOC中CD边上的高是( )
A.2
B.4
C.6
D.8
活动六、帮乐乐解决问题
乐乐做好了两个关于O点成中心对称的三角形,(△ABC,△DEF),却被顽皮的弟弟擦去了一部分,现在只剩下图中的图形,你能为他补出来吗?
活动七、课堂小结:??
1、本节课所学的内容有哪些?
中心对称的概念:要点是两个图形,一个中心,旋转180°,重合。
中心对称性质:(1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分(三点共线),(2).中心对称的两个图形是全等形
中心对称的应用:应用1、作中心对称图形;应用2、找出对称中心.
2、学完本节课后你还有哪些困惑??
活动八、布置作业
1、导学案完成23.2.1
教
学
设
计
新人教版九年级数学上册
第二十三章第二节中心对称
第1课时
任
志
辉
宁晋县高庄窠中学
一、教学内容:?
新人教版九年级数学上册第二十三章第二节中心对称第1课时
二、学情分析:?
1、学生是乡镇普通初中九年级的学生,班级学生学习方面存在一定的差异;但学生对数学抱有浓厚的兴趣。?
2、学生在前面已学习了图形的旋转变换,基本上掌握了旋转变换的性质;运用知识解决实际问题的能力和数学建模的能力还不强。?
3、对中心对称概念不易理解;归纳和运用性质也存在困难。?
三、教材分析:?
1、本节课选自人教社九年级数学上册23.2.1中心对称。?
2、中心对称是在学生已掌握旋转变换的基础上,由一般到特殊的方法归纳引出中心对称是特殊的旋转变换。在探索中心对称的概念、性质及应用上,让学生经历动手操作、观察、猜想、归纳等方法,进一步培养学生的自主学习能力以及合作、探究的精神,并在这个过程中增加一定的审美体验。?
3、中心对称承接平移、轴对称等知识,同时是下节学习中心对称图形的基础,又是后续学习几何的桥梁纽带。??
四、教学目标:?
(一)、知识技能:?
1、通过62页思考中图形旋转的演示理解中心对称、对称中心、关于中心的对称点的概念。?
2、结合探究掌握中心对称的性质,会依据中心对称的性质画出与已知图形成中心对称的图形。?
(二)、过程与方法:?
1、通过思考的观察培养学生的观察能力,经历探究性质的过程使学生获得基本的数学活动经验。?
2、通过画出与已知图形成中心对称的图形,进一步培养学生的尺规作图能力。?
(三)、情感、态度与价值观:?
让学生经历观察、操作等过程,理解中心对称的概念,从中心对称基本性质的探索活动,进一步发展学生空间观察能力.让学生通过独立思考,自主探究和合作交流,进一步体会中心对称的数学内涵,获得知识,体验成功。?
五、教学重点:?
中心对称的概念与性质及应用。
六、教学难点:?
中心对称的概念的导入与性质的探究。?
七、教学过程:?
教师引语,创设情境:?
我们生活在多姿多彩的图形世界中,小时候我们就对多姿多彩的图形充满兴趣与好奇,尤其是对运动变换的图形越加的好奇,我邻居家的乐乐对图形也充满着浓厚的兴趣,他画了一幅中心对称的图形,但是不小心被顽皮的弟弟用橡皮擦去了一部分,现在只剩下了这样的图形,于是他跪求!!!帮忙把他画的图形修复,我想让你们帮帮他。今天我们就带着帮助乐乐的爱心走进今天的数学课堂,23.2.1中心对称,学完本节课你将对图形的变换有一个全面深入的了解,也可以帮助乐乐修复他的图形了。下面让我们走进图形世界,走进中心对称。
我们这节课的学习目标
1.理解中心对称的定义.
2.探究中心对称的性质,感受中心对称美.
3.掌握中心对称的性质并利用中心对称的性质作图.
活动一:复习引入
观察图形变换。多媒体演示:旋转。?
幻灯片1是图形变换旋转,那么什么是图形的旋转?图形的旋转有哪些性质呢?学生根据幻灯片的演示回答这些问题。
1、图形的旋转定义:在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形变换叫做图形的旋转,这个定点称为旋转中心,旋转的角度称为旋转角。
2、图形的旋转有哪些性质?
(1)、旋转前后的图形全等;?
????(2)、对应点到旋转中心的距离相等;??
(3)、对应点与旋转中心所连线段的夹角等于旋转角。
生活中有没有旋转角是180度的旋转图形呢?本节课我们就来探究旋转角是180度的旋转图形。?
活动二:创设情景,探索新知.
1.问题:观察实例,回答问题:
①把其中一个图案绕点O旋转180°,你有什么发现?
②线段AC与BD相交于点O,OA=OC,OB=OD,把△AOB绕点O旋转
180?,你有什么发现?
2.引导学生归纳出中心对称的定义:把一个图形绕
旋转
,如果它能够
,那么就说这两个图形
或
;点O叫做
;这两个图形中的对应点叫做关于中心的
.如问题②中的点
与点
、点
与点
、点
与点
。
中心对称的定义要点:(两个图形,一个中心,旋转180度,重合?)
活动三、动手操作,理解性质.
1.问题:如课本第63页图23.2-3,
旋转三角板,画关于点O对称的两个三角形:(1)
画出△ABC;(2)
以三角板的一个顶点O为中心,把三角板旋转180?,画出△A′B′C′.移除三角板。
2.让学生在作图的基础上思考:
(1)分别连接对应点AA′、
BB′、CC′.点O在线段AA′上吗?如果在,在什么位置?
(2)
△ABC与△A′B′C′全等吗?为什么?
(3)
通过对问题(1)、
(2)的研究,你能从中得到什么结论?
3.师生合作,归纳出中心对称的性质:
(1)中心对称的两个图形,对称点所连线段都
,而且
;(三点共线)
(2)中心对称的两个图形是
.
下图中△A'B'C'与△ABC关于点O是成中心对称的,你能从图中找到那些等量关系?(多媒体出示图形),发挥学生的想象,尽可能说出多种等量的关系。包含边、角和全等。
活动四、知识应用,学生动手操作。
1、例题:
如图,选择点O为对称中心,画出点A关于点O的对称点A′;
A.
O.
2、如图,选择点O为对称中心,画出线段AB关于点O的对称线段A′B′;
(2)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
(分析)
(1)假设点A的对称点A′已经作出,那么连接
A
A′,则这条线段一定经过点
,且
=
。你找到作图方法了吗
?
(2)确定一条线段需要几个点?作一条线段关于某点成中心对称的线段,需要作几个点的
对称点呢?
(3)确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
例2.如图,已知△ABC与△A′B′C′中心对称,求出它们的对称中心O.
解法1:根据观察,B、B′应是对应点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如多媒体演示)
解法2:根据观察,B、B′及C、C′应是两组对应点,连接BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如多媒体演示).
活动五、知识运用,中考链接
1.下所英文单词中,是中心对称的有
(
)
A.CEO
B.MBA
C.SOS
D.SAR
如图,已知△AOB与△DOC成中心对称,△AOB的面积
是6,
AB=3,则△DOC中CD边上的高是( )
A.2
B.4
C.6
D.8
活动六、帮乐乐解决问题
乐乐做好了两个关于O点成中心对称的三角形,(△ABC,△DEF),却被顽皮的弟弟擦去了一部分,现在只剩下图中的图形,你能为他补出来吗?
活动七、课堂小结:??
1、本节课所学的内容有哪些?
中心对称的概念:要点是两个图形,一个中心,旋转180°,重合。
中心对称性质:(1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分(三点共线),(2).中心对称的两个图形是全等形
中心对称的应用:应用1、作中心对称图形;应用2、找出对称中心.
2、学完本节课后你还有哪些困惑??
活动八、布置作业
1、导学案完成23.2.1
教
学
设
计
新人教版九年级数学上册
第二十三章第二节中心对称
第1课时
任
志
辉
宁晋县高庄窠中学
同课章节目录
