苏科版八年级上册 第三章 勾股定理 提优微专题复习二(word版,无答案)
文档属性
| 名称 | 苏科版八年级上册 第三章 勾股定理 提优微专题复习二(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 552.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 06:38:34 | ||
图片预览


文档简介
微专题:勾股定理有关的路径、展开图问题
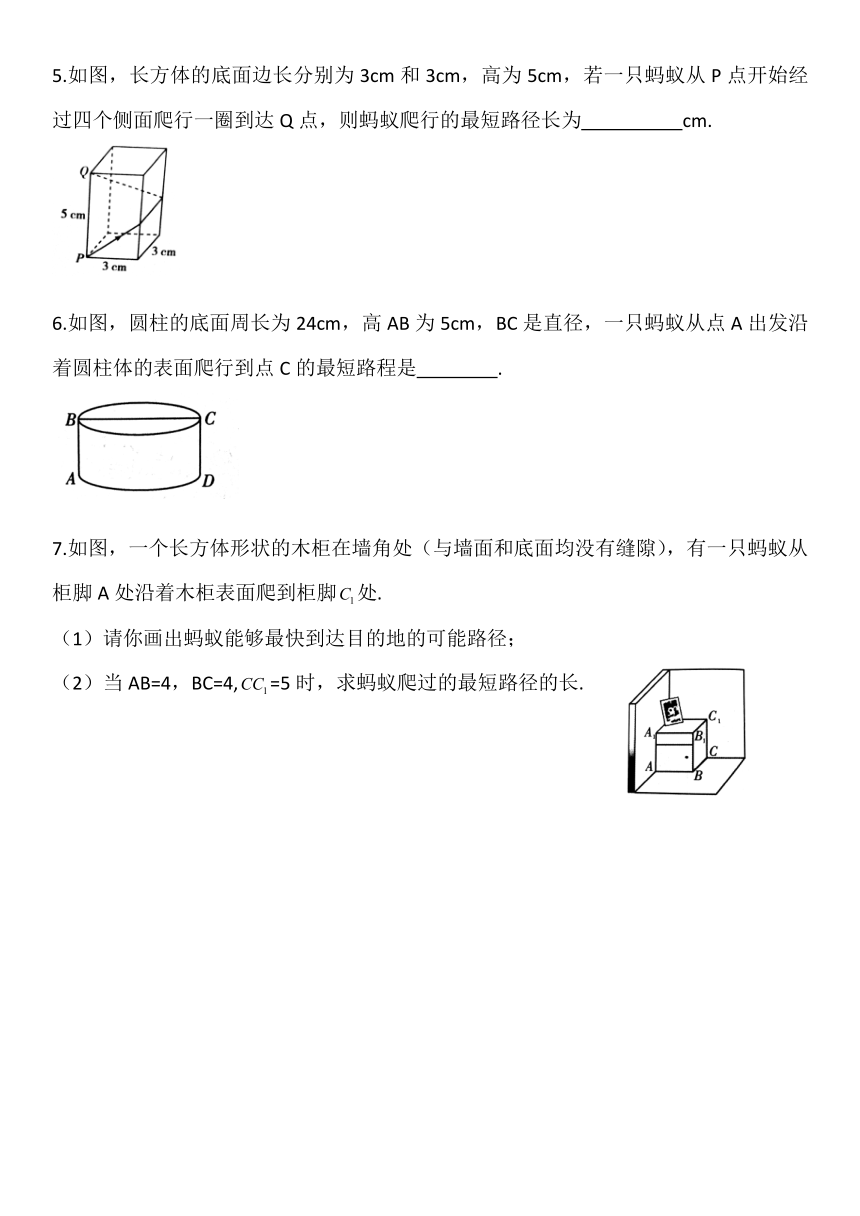
1.如图①中的一块砖的宽AN=5cm,长ND=10cm,CD上的点B距地面的高度BD=8cm.地面上A处的一只蚂蚁要到B处吃食,需爬行的最短路径是
.
2.如图所示,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=BC.一直蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是
.
3.我国古代有这样一道数学问题:“枯木一根直立地方,高二丈,周三尺,问葛藤自跟缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看做一个圆柱体,因一丈是十尺,则该圆柱的高是20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
尺.
4.如图,圆柱形玻璃杯高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为
cm.
5.如图,长方体的底面边长分别为3cm和3cm,高为5cm,若一只蚂蚁从P点开始经过四个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为
cm.
6.如图,圆柱的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是
.
7.如图,一个长方体形状的木柜在墙角处(与墙面和底面均没有缝隙),有一只蚂蚁从柜脚A处沿着木柜表面爬到柜脚处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,=5时,求蚂蚁爬过的最短路径的长.
微专题:勾股定理有关的噪声、龙卷风影响问题
1.台风是一种自然灾害,它以台风中心为圆心,在周围的数十千米范围内形成气旋风暴,有极强的破坏力.如图,据气象观测,在距沿海城市A的正南方向240km处的B处有台风中心,其中心最大风力为12级,每远离台风中心25km,风力就会削弱一级,该台风中心正以25km/h的速度沿北偏东30°方向向C移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到台风影响,请说明理由;
(2)若受到台风影响,则台风影响该市的持续时间有多长?
2.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=240m,当火车在铁路MN上沿ON方向行驶时,周围200m以内会受到噪音的影响,如果行驶的速度为72km/h,求居民楼受噪音影响的时间.
3.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路PON方向行驶一次给学校A带来的噪声影响.
4.如图,A城气象台测得台风中心在A城正西方向600km处的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受到台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭到这次台风影响的时间有多长?
微专题:勾股定理有关翻折问题
1.
如图所示,有一块直角纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边直角边AC的延长线上的点E处,折痕为AD,则CE的长为
.
2.如图,在长方形纸片ABCD中,已知AD=8,折叠纸片,使对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为
.
3.如图,正方形纸片ABCD的边长为3,点
E、F分别在边BC,CD上,将AB,AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为
.
4.已知,已知Rt△ABC中,∠C=90°,AC=6,BC=8将它的锐角A翻折,使点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的值为
.
5.如图,长方形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是
.
6.如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP=
.
7.如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
8.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
9.如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.
(1)求∠AEC+∠AGC的度数;
(2)求证:BG=GC.
10.如图①,在一张长方形纸片ABCD上任意画一条线段GF,将纸片沿线段GF折叠,
(1)重叠部分的△EFG是等腰三角形吗?请说明理由.
(2)若使点C与点A重合,折痕为GF,如图②,△AFG的面积为,图③中沿BD折叠,△EBD的面积为,试问和相等吗?请说明理由.
11.如图,折叠长方形纸片ABCD,使点D落在BC上的点F处,折痕为AE,已知该纸片宽AB=6cm,长BC=10cm.
(1)求EC的长;
(2)若在折痕AE上存在一点P到边BC的距离与到点D的距离相等,则此相等的距离为
cm.
1.如图①中的一块砖的宽AN=5cm,长ND=10cm,CD上的点B距地面的高度BD=8cm.地面上A处的一只蚂蚁要到B处吃食,需爬行的最短路径是
.
2.如图所示,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=BC.一直蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是
.
3.我国古代有这样一道数学问题:“枯木一根直立地方,高二丈,周三尺,问葛藤自跟缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看做一个圆柱体,因一丈是十尺,则该圆柱的高是20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
尺.
4.如图,圆柱形玻璃杯高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为
cm.
5.如图,长方体的底面边长分别为3cm和3cm,高为5cm,若一只蚂蚁从P点开始经过四个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为
cm.
6.如图,圆柱的底面周长为24cm,高AB为5cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是
.
7.如图,一个长方体形状的木柜在墙角处(与墙面和底面均没有缝隙),有一只蚂蚁从柜脚A处沿着木柜表面爬到柜脚处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,=5时,求蚂蚁爬过的最短路径的长.
微专题:勾股定理有关的噪声、龙卷风影响问题
1.台风是一种自然灾害,它以台风中心为圆心,在周围的数十千米范围内形成气旋风暴,有极强的破坏力.如图,据气象观测,在距沿海城市A的正南方向240km处的B处有台风中心,其中心最大风力为12级,每远离台风中心25km,风力就会削弱一级,该台风中心正以25km/h的速度沿北偏东30°方向向C移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到台风影响,请说明理由;
(2)若受到台风影响,则台风影响该市的持续时间有多长?
2.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=240m,当火车在铁路MN上沿ON方向行驶时,周围200m以内会受到噪音的影响,如果行驶的速度为72km/h,求居民楼受噪音影响的时间.
3.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路PON方向行驶一次给学校A带来的噪声影响.
4.如图,A城气象台测得台风中心在A城正西方向600km处的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受到台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭到这次台风影响的时间有多长?
微专题:勾股定理有关翻折问题
1.
如图所示,有一块直角纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边直角边AC的延长线上的点E处,折痕为AD,则CE的长为
.
2.如图,在长方形纸片ABCD中,已知AD=8,折叠纸片,使对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为
.
3.如图,正方形纸片ABCD的边长为3,点
E、F分别在边BC,CD上,将AB,AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为
.
4.已知,已知Rt△ABC中,∠C=90°,AC=6,BC=8将它的锐角A翻折,使点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的值为
.
5.如图,长方形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是
.
6.如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP=
.
7.如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
8.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
9.如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,G为BC上的一点,将△ADE沿AE对折至△AFE,同时将△ABG沿AG对折至△AFG,连接CF.
(1)求∠AEC+∠AGC的度数;
(2)求证:BG=GC.
10.如图①,在一张长方形纸片ABCD上任意画一条线段GF,将纸片沿线段GF折叠,
(1)重叠部分的△EFG是等腰三角形吗?请说明理由.
(2)若使点C与点A重合,折痕为GF,如图②,△AFG的面积为,图③中沿BD折叠,△EBD的面积为,试问和相等吗?请说明理由.
11.如图,折叠长方形纸片ABCD,使点D落在BC上的点F处,折痕为AE,已知该纸片宽AB=6cm,长BC=10cm.
(1)求EC的长;
(2)若在折痕AE上存在一点P到边BC的距离与到点D的距离相等,则此相等的距离为
cm.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
