题型分类学案:利用导数求函数单调性(含答案)
文档属性
| 名称 | 题型分类学案:利用导数求函数单调性(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
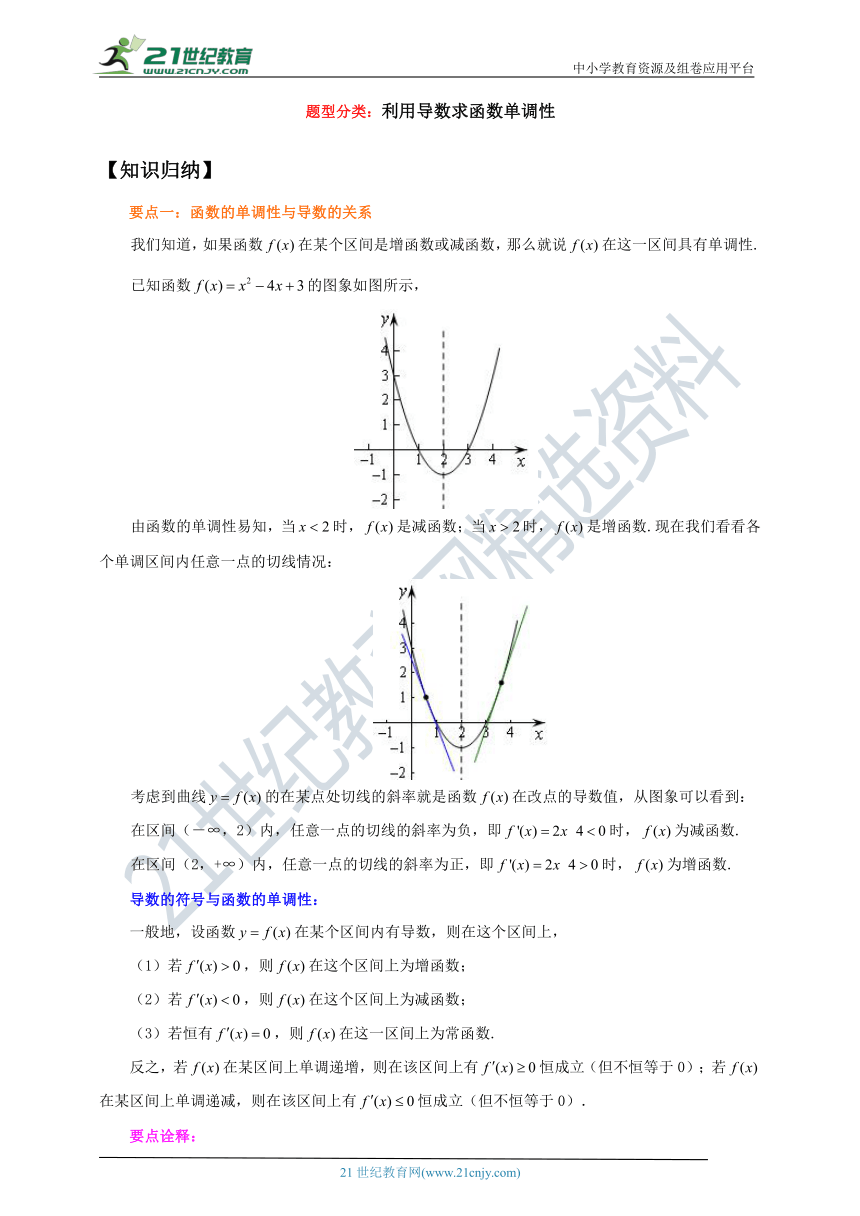
题型分类:利用导数求函数单调性
【知识归纳】
要点一:函数的单调性与导数的关系
我们知道,如果函数在某个区间是增函数或减函数,那么就说在这一区间具有单调性.
已知函数的图象如图所示,
由函数的单调性易知,当时,是减函数;当时,是增函数.现在我们看看各个单调区间内任意一点的切线情况:
考虑到曲线的在某点处切线的斜率就是函数在改点的导数值,从图象可以看到:
在区间(-∞,2)内,任意一点的切线的斜率为负,即时,为减函数.
在区间(2,+∞)内,任意一点的切线的斜率为正,即时,为增函数.
导数的符号与函数的单调性:
一般地,设函数在某个区间内有导数,则在这个区间上,
(1)若,则在这个区间上为增函数;
(2)若,则在这个区间上为减函数;
(3)若恒有,则在这一区间上为常函数.
反之,若在某区间上单调递增,则在该区间上有恒成立(但不恒等于0);若在某区间上单调递减,则在该区间上有恒成立(但不恒等于0).
要点诠释:
①因为导数的几何意义是曲线切线的斜率,故当在某区间上,即切线斜率为正时,函数在这个区间上为增函数;当在某区间上,即切线斜率为负时,函数在这个区间上为减函数;即导函数的正负决定了原函数的增减;
②若在某区间上有有限个点使,在其余点恒有,则仍为增函数(减函数的情形完全类似.
即在某区间上,在这个区间上为增函数;
在这个区间上为减函数,但反之不成立.
③在某区间上为增函数在该区间;
在某区间上为减函数在该区间.
在区间(,b)内,(或)是在区间(,b)内单调递增(或减)的充分不必要条件.
例如:而f()在R上递增.
④只有在某区间内恒有,这个函数在这个区间上才为常数函数.
⑤注意导函数图象与原函数图象之间的关系.
要点二:利用导数研究函数的单调性
利用导数判断函数单调性的基本方法:
设函数在区间(,b)内可导,
(1)如果恒有,则函数在(,b)内为增函数;
(2)如果恒有,则函数在(,b)内为减函数;
(3)如果恒有,则函数在(,b)内为常数函数.
要点诠释:
①若函数在区间(,b)内单调递增,则,若函数在(,b)内单调递减,则;
②或恒成立,求参数值的范围的方法——分离参数法:或.
要点三:利用导数求函数单调区间的基本步骤
(1)确定函数的定义域;
(2)求导数;
(3)在函数的定义域内解不等式或;
(4)确定的单调区间.
或者:令,求出它在定义域内的一切实数根。把这些实数根和函数的间断点(即的无定义点)的横坐标按从小到大的顺序排列起来,然后用这些点把函数的定义区间分成若干个小区间,判断在各个小区间内的符号.
要点诠释:
①求函数单调区间时,要注意单调区间一定是函数定义域的子集;
②求单调区间常常通过列表的方法进行求解,使解题思路步骤更加清晰、明确.
【典型剖析】
类型一:求普通函数的最值
例1. 函数在区间上的最小值为( )
A. B. C. D.
答案:D;
得而端点的函数值,得
【变式1】已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大的年利润的年产量为( )
A.13万件 B.11万件 C.9万件 D.7万件
答案:C;
[解析] 本题考查了导数的应用及求导运算.
∵x>0,y′=-x2+81=(9-x)(9+x),
令y′=0,解得x=9,所以x∈(0,9)时,y′>0,
x∈(9,+∞)时,y′<0,y先增后减.
∴x=9时函数取最大值,选C,属导数法求最值问题.
【变式2】若函数f(x)=(a>0)在[1,+∞)上的最大值为,则a的值为________.
[答案] -1
[解析] f′(x)==
令f′(x)=0,解得x=或x=-(舍去)
当x>时,f′(x)<0;当00;
当x=时,f(x)==,=<1,不合题意.
∴f(x)max=f(1)==,解得a=-1.
【变式3】求函数的最值
思路:首先判定定义域为,对函数进行求导,根据单调区间求出函数的最值
解:,令,解得:
的单调区间为:
,无最小值
【变式4】已知函数,是否存在实数,使得在上取得最大值,最小值若存在,求出的值,若不存在,请说明理由
思路:利用求出函数的单调区间,在根据单调区间判断最大最小值点的可能位置,进而根据最大最小值解出
解:,
(1)当时,
在单调递减
(2)当时,
在单调递增
或
类型二、导数图像与函数图像的应用
例2.已知二次函数的图象如图1所示 , 则其导函数的图象大致形状是( )
答案:B;
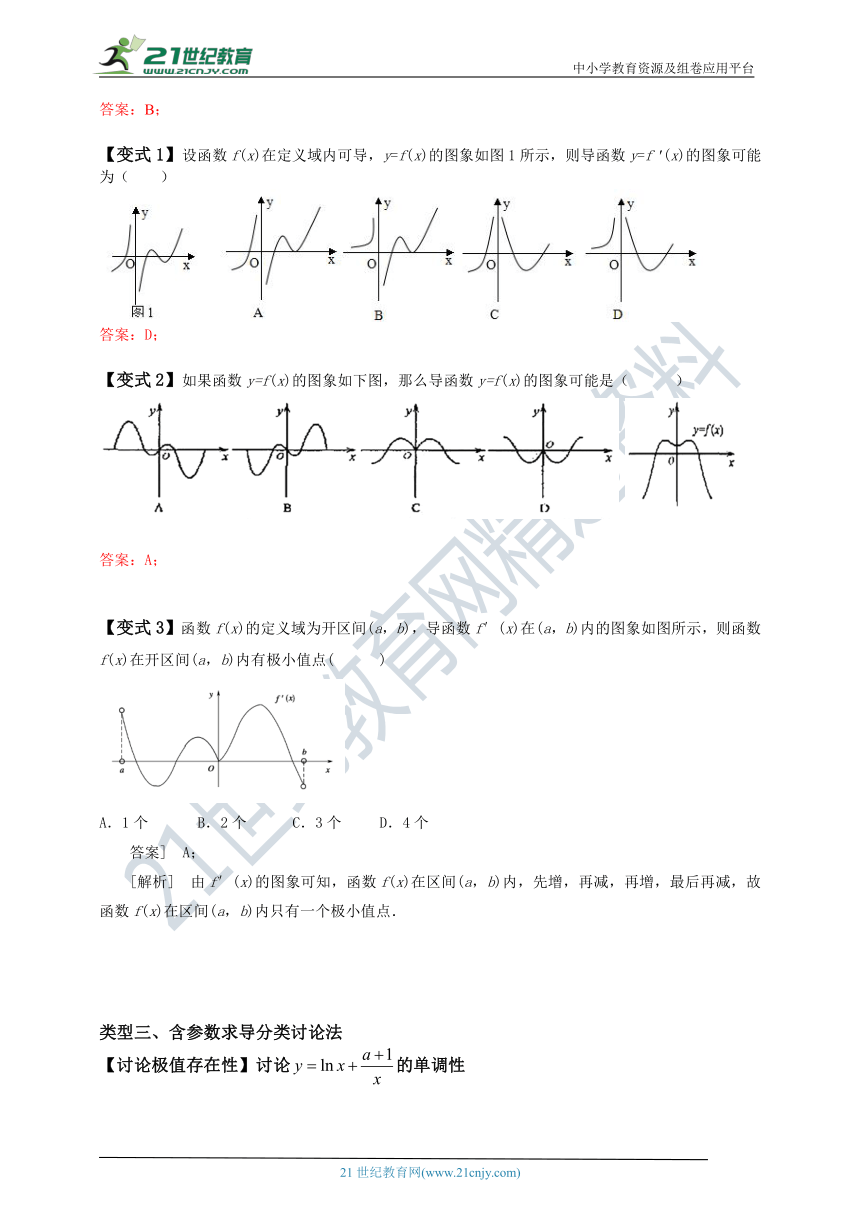
【变式1】设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,则导函数y=f (x)的图象可能为( )
答案:D;
【变式2】如果函数y=f(x)的图象如下图,那么导函数y=f(x)的图象可能是( )
答案:A;
【变式3】函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
A.1个 B.2个 C.3个 D.4个
答案] A;
[解析] 由f′(x)的图象可知,函数f(x)在区间(a,b)内,先增,再减,再增,最后再减,故函数f(x)在区间(a,b)内只有一个极小值点.
类型三、含参数求导分类讨论法
【讨论极值存在性】讨论的单调性
【讨论极值大小关系】讨论的单调性
【变式1】已知函数,求的单调区间
解:定义域
令,所解不等式为
当时,即解不等式
的单调区间为:
当时, 恒成立
为增函数:
【变式2】讨论函数的单调区间
解: 令
即 (注意定义域为,所以导函数分母恒正,去掉后简化所解不等式)
① 时 (求解需要除以后开方,进而两个地方均需要分类讨论,先从的符号入手)
恒成立,在单调递增
② 函数 为增函数
③ 时 (下一步为开方出解集,按的符号进行再分类)
当即时,恒成立,在单调递减
当即时,解得:
的单调区间为:
【变式3】已知函数,讨论的单调性
解:定义域为
令即
考虑 (左边无法直接因式分解,考虑二次函数是否与轴有交点)
① 时 恒成立,故在单调递增
② 时 的解
的解集为
的单调区间为:
③ 时
在单调递增
【变式4】已知函数.求函数的单调区间.
解:
令,即,
(参数角色:① 的大小,② 是否在定义域内,以①为目标分类)
① 即 (此时一定在定义域中,故不再分类)
不等式的解集为或 的单调区间为:
↗ ↘ ↗
② 在单调递增
③ ,要根据是否在进行进一步分类
当时, 不等式的解集为或
的单调区间为:
↗ ↘ ↗
当时,则,不等式的解集为 ,的单调区间为:
↘ ↗
类型四、单调性逆应用
孤立系数法求系数范围:
知道单调性反求系数,多数用孤立系数法。具体操作步骤如下:
1、求导;
2、若要求单调递增,则令导数大于等于“0”;若要求单调递减,则令导数小于等于“0”;
3、整理式子,把所要求的系数放在左边,其他放在右边;
4、若,则求最大值;若,则求最小值;
5、该系数大于(或小于)该最值;
例4.若函数在区间上是减函数,则实数的范围是( )
A. B、 C、 D、
答案:A
【变式1】函数f(x)=x3+ax-2在区间[1,+∞)上是增函数,则实数a的取值范围是( )
A.[3,+∞) B.[-3,+∞) C.(-3,+∞) D.(-∞,-3)
[答案] B
[解析] ∵f(x)=x3+ax-2在[1,+∞)上是增函数,∴f′(x)=3x2+a≥0在[1,+∞)上恒成立
即a≥-3x2在[1,+∞)上恒成立
又∵在[1,+∞)上(-3x2)max=-3
∴a≥-3,故应选B.
【变式2】若上是减函数,则的取值范围是( )
A. B. C. D.
答案: C
【变式3】已知函数在区间上是增函数,则实数的取值范围为( )
A. B. C. D.
【答案】D
【解析】 因为函数在区间上是增函数,所以在上恒成立,即在上恒成立,易知在上单调递减,所以,所以,解得.
【变式4】若函数y=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围是_________.
[答案] [3,+∞)
[解析] y′=3x2-2ax,由题意知3x2-2ax<0在区间(0,2)内恒成立,
即a>x在区间(0,2)上恒成立,∴a≥3.
【变式5】函数在上单调递增,则实数的取值范围是 .
答案:4 ;
【变式6】函数在上单调递增,则实数的取值范围是 .
答案:;
.
_21?????????è?????(www.21cnjy.com)_
题型分类:利用导数求函数单调性
【知识归纳】
要点一:函数的单调性与导数的关系
我们知道,如果函数在某个区间是增函数或减函数,那么就说在这一区间具有单调性.
已知函数的图象如图所示,
由函数的单调性易知,当时,是减函数;当时,是增函数.现在我们看看各个单调区间内任意一点的切线情况:
考虑到曲线的在某点处切线的斜率就是函数在改点的导数值,从图象可以看到:
在区间(-∞,2)内,任意一点的切线的斜率为负,即时,为减函数.
在区间(2,+∞)内,任意一点的切线的斜率为正,即时,为增函数.
导数的符号与函数的单调性:
一般地,设函数在某个区间内有导数,则在这个区间上,
(1)若,则在这个区间上为增函数;
(2)若,则在这个区间上为减函数;
(3)若恒有,则在这一区间上为常函数.
反之,若在某区间上单调递增,则在该区间上有恒成立(但不恒等于0);若在某区间上单调递减,则在该区间上有恒成立(但不恒等于0).
要点诠释:
①因为导数的几何意义是曲线切线的斜率,故当在某区间上,即切线斜率为正时,函数在这个区间上为增函数;当在某区间上,即切线斜率为负时,函数在这个区间上为减函数;即导函数的正负决定了原函数的增减;
②若在某区间上有有限个点使,在其余点恒有,则仍为增函数(减函数的情形完全类似.
即在某区间上,在这个区间上为增函数;
在这个区间上为减函数,但反之不成立.
③在某区间上为增函数在该区间;
在某区间上为减函数在该区间.
在区间(,b)内,(或)是在区间(,b)内单调递增(或减)的充分不必要条件.
例如:而f()在R上递增.
④只有在某区间内恒有,这个函数在这个区间上才为常数函数.
⑤注意导函数图象与原函数图象之间的关系.
要点二:利用导数研究函数的单调性
利用导数判断函数单调性的基本方法:
设函数在区间(,b)内可导,
(1)如果恒有,则函数在(,b)内为增函数;
(2)如果恒有,则函数在(,b)内为减函数;
(3)如果恒有,则函数在(,b)内为常数函数.
要点诠释:
①若函数在区间(,b)内单调递增,则,若函数在(,b)内单调递减,则;
②或恒成立,求参数值的范围的方法——分离参数法:或.
要点三:利用导数求函数单调区间的基本步骤
(1)确定函数的定义域;
(2)求导数;
(3)在函数的定义域内解不等式或;
(4)确定的单调区间.
或者:令,求出它在定义域内的一切实数根。把这些实数根和函数的间断点(即的无定义点)的横坐标按从小到大的顺序排列起来,然后用这些点把函数的定义区间分成若干个小区间,判断在各个小区间内的符号.
要点诠释:
①求函数单调区间时,要注意单调区间一定是函数定义域的子集;
②求单调区间常常通过列表的方法进行求解,使解题思路步骤更加清晰、明确.
【典型剖析】
类型一:求普通函数的最值
例1. 函数在区间上的最小值为( )
A. B. C. D.
答案:D;
得而端点的函数值,得
【变式1】已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大的年利润的年产量为( )
A.13万件 B.11万件 C.9万件 D.7万件
答案:C;
[解析] 本题考查了导数的应用及求导运算.
∵x>0,y′=-x2+81=(9-x)(9+x),
令y′=0,解得x=9,所以x∈(0,9)时,y′>0,
x∈(9,+∞)时,y′<0,y先增后减.
∴x=9时函数取最大值,选C,属导数法求最值问题.
【变式2】若函数f(x)=(a>0)在[1,+∞)上的最大值为,则a的值为________.
[答案] -1
[解析] f′(x)==
令f′(x)=0,解得x=或x=-(舍去)
当x>时,f′(x)<0;当0
当x=时,f(x)==,=<1,不合题意.
∴f(x)max=f(1)==,解得a=-1.
【变式3】求函数的最值
思路:首先判定定义域为,对函数进行求导,根据单调区间求出函数的最值
解:,令,解得:
的单调区间为:
,无最小值
【变式4】已知函数,是否存在实数,使得在上取得最大值,最小值若存在,求出的值,若不存在,请说明理由
思路:利用求出函数的单调区间,在根据单调区间判断最大最小值点的可能位置,进而根据最大最小值解出
解:,
(1)当时,
在单调递减
(2)当时,
在单调递增
或
类型二、导数图像与函数图像的应用
例2.已知二次函数的图象如图1所示 , 则其导函数的图象大致形状是( )
答案:B;
【变式1】设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,则导函数y=f (x)的图象可能为( )
答案:D;
【变式2】如果函数y=f(x)的图象如下图,那么导函数y=f(x)的图象可能是( )
答案:A;
【变式3】函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
A.1个 B.2个 C.3个 D.4个
答案] A;
[解析] 由f′(x)的图象可知,函数f(x)在区间(a,b)内,先增,再减,再增,最后再减,故函数f(x)在区间(a,b)内只有一个极小值点.
类型三、含参数求导分类讨论法
【讨论极值存在性】讨论的单调性
【讨论极值大小关系】讨论的单调性
【变式1】已知函数,求的单调区间
解:定义域
令,所解不等式为
当时,即解不等式
的单调区间为:
当时, 恒成立
为增函数:
【变式2】讨论函数的单调区间
解: 令
即 (注意定义域为,所以导函数分母恒正,去掉后简化所解不等式)
① 时 (求解需要除以后开方,进而两个地方均需要分类讨论,先从的符号入手)
恒成立,在单调递增
② 函数 为增函数
③ 时 (下一步为开方出解集,按的符号进行再分类)
当即时,恒成立,在单调递减
当即时,解得:
的单调区间为:
【变式3】已知函数,讨论的单调性
解:定义域为
令即
考虑 (左边无法直接因式分解,考虑二次函数是否与轴有交点)
① 时 恒成立,故在单调递增
② 时 的解
的解集为
的单调区间为:
③ 时
在单调递增
【变式4】已知函数.求函数的单调区间.
解:
令,即,
(参数角色:① 的大小,② 是否在定义域内,以①为目标分类)
① 即 (此时一定在定义域中,故不再分类)
不等式的解集为或 的单调区间为:
↗ ↘ ↗
② 在单调递增
③ ,要根据是否在进行进一步分类
当时, 不等式的解集为或
的单调区间为:
↗ ↘ ↗
当时,则,不等式的解集为 ,的单调区间为:
↘ ↗
类型四、单调性逆应用
孤立系数法求系数范围:
知道单调性反求系数,多数用孤立系数法。具体操作步骤如下:
1、求导;
2、若要求单调递增,则令导数大于等于“0”;若要求单调递减,则令导数小于等于“0”;
3、整理式子,把所要求的系数放在左边,其他放在右边;
4、若,则求最大值;若,则求最小值;
5、该系数大于(或小于)该最值;
例4.若函数在区间上是减函数,则实数的范围是( )
A. B、 C、 D、
答案:A
【变式1】函数f(x)=x3+ax-2在区间[1,+∞)上是增函数,则实数a的取值范围是( )
A.[3,+∞) B.[-3,+∞) C.(-3,+∞) D.(-∞,-3)
[答案] B
[解析] ∵f(x)=x3+ax-2在[1,+∞)上是增函数,∴f′(x)=3x2+a≥0在[1,+∞)上恒成立
即a≥-3x2在[1,+∞)上恒成立
又∵在[1,+∞)上(-3x2)max=-3
∴a≥-3,故应选B.
【变式2】若上是减函数,则的取值范围是( )
A. B. C. D.
答案: C
【变式3】已知函数在区间上是增函数,则实数的取值范围为( )
A. B. C. D.
【答案】D
【解析】 因为函数在区间上是增函数,所以在上恒成立,即在上恒成立,易知在上单调递减,所以,所以,解得.
【变式4】若函数y=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围是_________.
[答案] [3,+∞)
[解析] y′=3x2-2ax,由题意知3x2-2ax<0在区间(0,2)内恒成立,
即a>x在区间(0,2)上恒成立,∴a≥3.
【变式5】函数在上单调递增,则实数的取值范围是 .
答案:4 ;
【变式6】函数在上单调递增,则实数的取值范围是 .
答案:;
.
_21?????????è?????(www.21cnjy.com)_
