三角形全等判定(HL)公开课
文档属性
| 名称 | 三角形全等判定(HL)公开课 |

|
|
| 格式 | rar | ||
| 文件大小 | 149.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-21 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
学习目标:
1、掌握“斜边、直角边”的判定方法。
2、会运用“斜边、直角边”的判定方法证明直角三角形全等的简单问题。
重难点:
会运用“斜边、直角边”的判定方法证明直角三角形全等的简单问题。
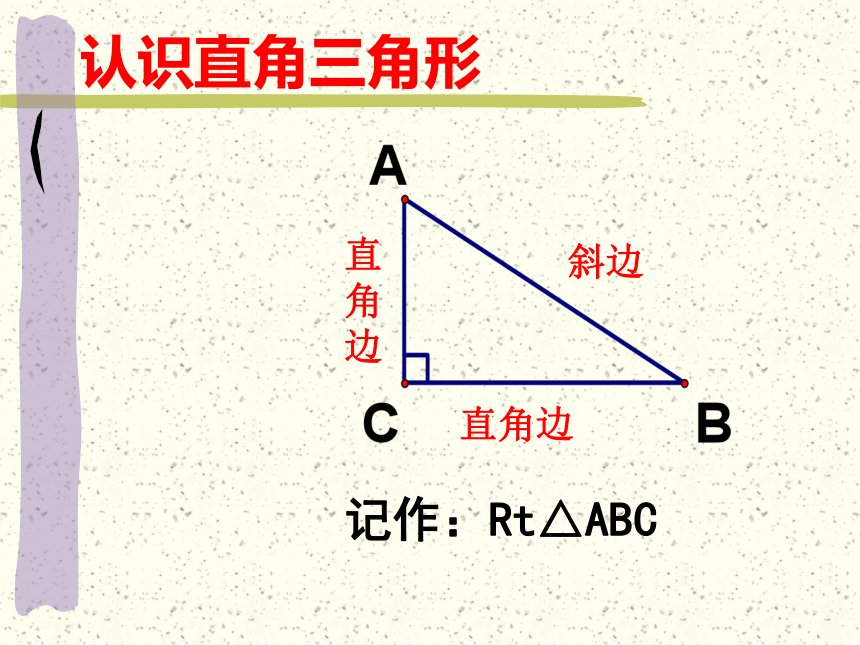
认识直角三角形
直角边
直角边
斜边
记作:Rt△ABC
A
C
B
D
F
E
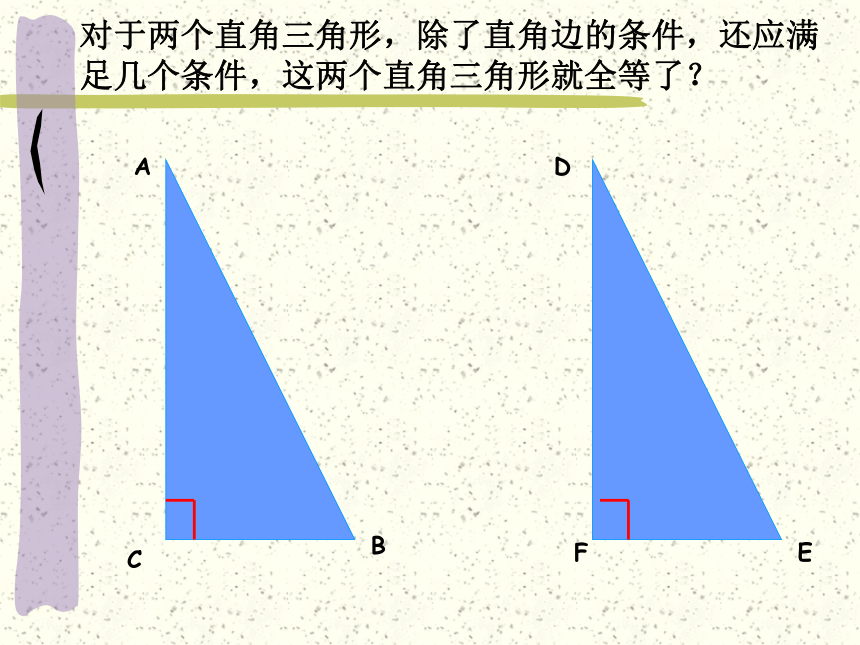
对于两个直角三角形,除了直角边的条件,还应满足几个条件,这两个直角三角形就全等了?
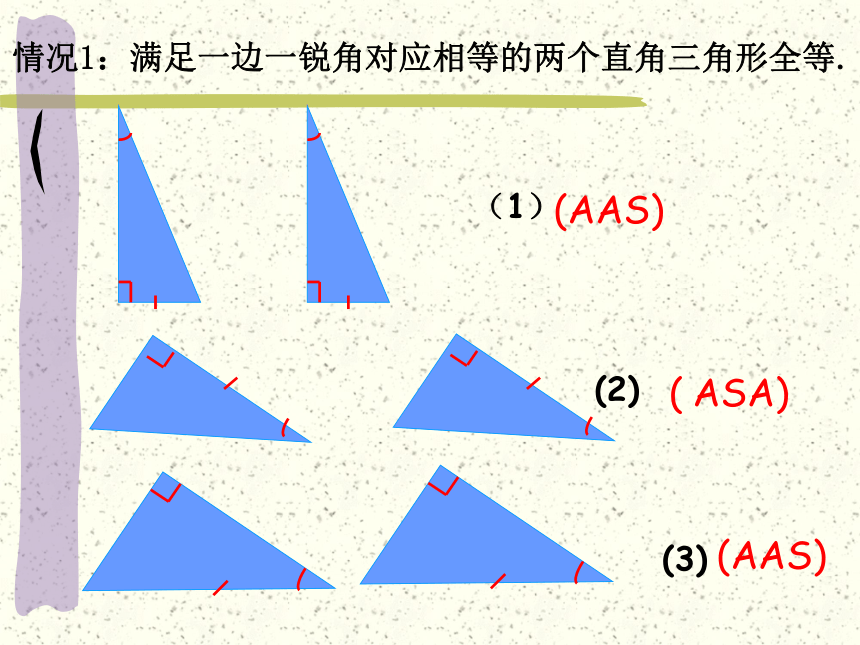
情况1:满足一边一锐角对应相等的两个直角三角形全等.
(1)
(2)
(3)
(AAS)
( ASA)
(AAS)
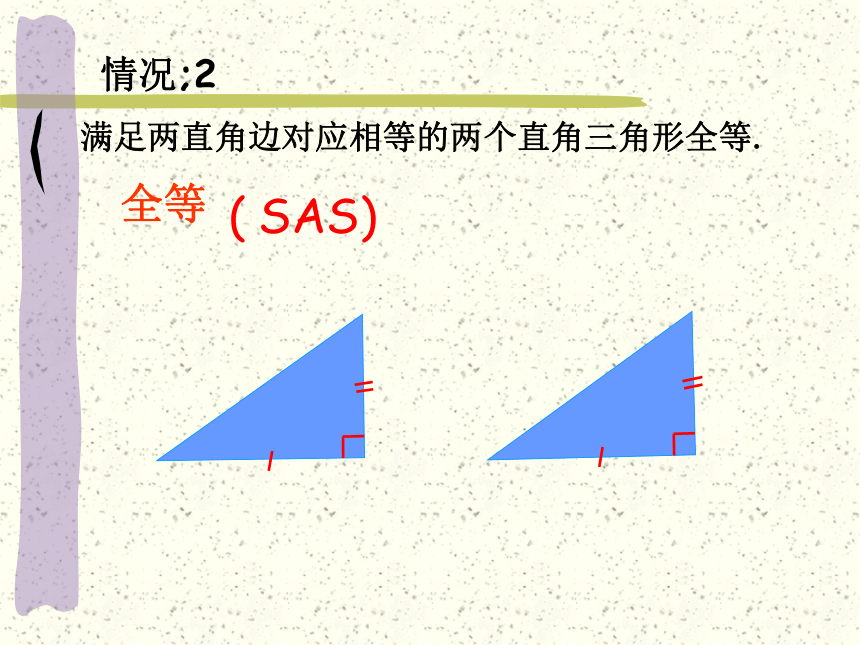
满足两直角边对应相等的两个直角三角形全等.
全等
( SAS)
情况;2
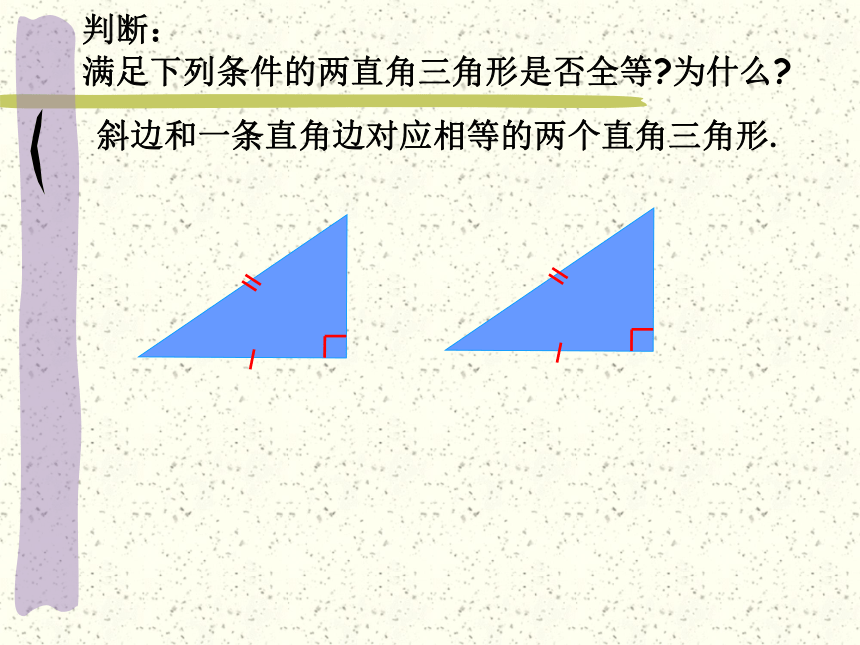
斜边和一条直角边对应相等的两个直角三角形.
判断:
满足下列条件的两直角三角形是否全等 为什么
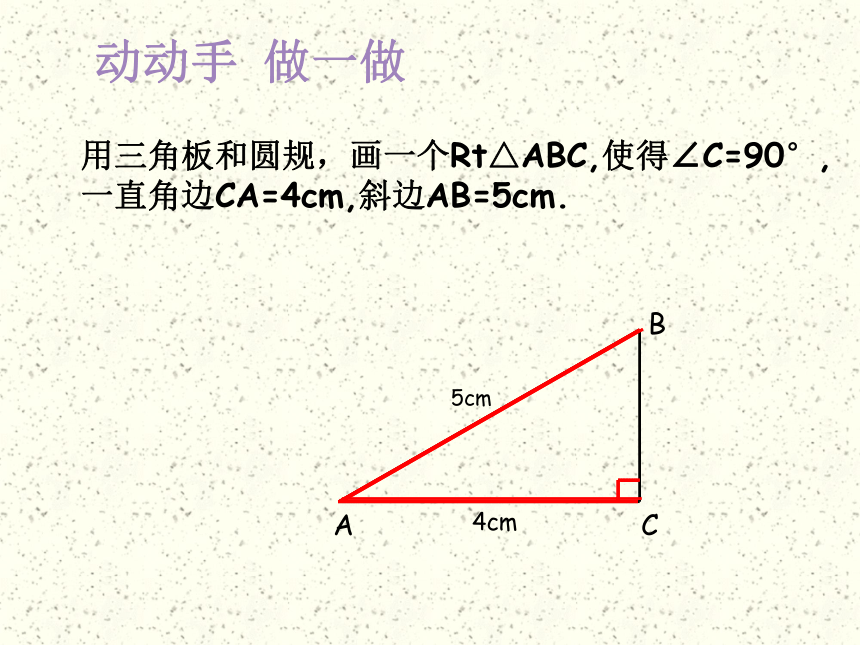
动动手 做一做
用三角板和圆规,画一个Rt△ABC,使得∠C=90°,一直角边CA=4cm,斜边AB=5cm.
A
B
C
5cm
4cm
动动手 做一做
Step1:画∠MCN=90°;
C
N
M
动动手 做一做
Step1:画∠MCN=90°;
C
N
M
Step2:在射线CM上截取CA=4cm;
A
Step1:画∠MCN=90°;
Step2:在射线CM上截取CA=4cm;
动动手 做一做
Step3:以A为圆心,5cm为半径画弧,交射线CN于B;
C
N
M
A
B
Step1:画∠MCN=90°;
C
N
M
Step2:在射线CM上截取CA=4cm;
B
动动手 做一做
Step3:以A为圆心,5cm为半径画弧,交射线CN于B;
A
Step4:连结AB;
△ABC即为所要画的三角形
动动手 做一做 比比看
把我们刚画好的直角三角形剪下来,和同桌的比比看,
这些直角三角形有怎样的关系呢?
Rt△ABC≌
A
B
C
5cm
4cm
A′
B ′
C ′
5cm
4cm
斜边和一条直角边对应相等的两个直角三角形全等.
(简写成“斜边、直角边”
或“HL”)
说明:
1、只能用于证明直角三角形的全等。
hypotenuse 斜边 leg 直角边
2、SSS、SAS、ASA、AAS适用于任何三角形,
包括直角三角形。
例1
已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.
A
B
D
C
证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)
A
已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: BC=AD.
A
B
D
C
证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)
A
变式延伸
∴BC=AD.
小试牛刀
已知:AB=CD,AE⊥BC,DF⊥BC ,CE=BF,
求证:AE=DF
C
D
A
B
F
E
课堂小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
应用
“ SSS ”
已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形.
D
B
C
A
F
E
学以致用
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
学以致用
先把它转化为一个纯数学问题:
已知:如图,AC=DF,AC⊥AB,DE⊥DF.
求证:∠ABC=∠DFE.
课后作业
作业本:
课本14页 练习:1
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
学习目标:
1、掌握“斜边、直角边”的判定方法。
2、会运用“斜边、直角边”的判定方法证明直角三角形全等的简单问题。
重难点:
会运用“斜边、直角边”的判定方法证明直角三角形全等的简单问题。
认识直角三角形
直角边
直角边
斜边
记作:Rt△ABC
A
C
B
D
F
E
对于两个直角三角形,除了直角边的条件,还应满足几个条件,这两个直角三角形就全等了?
情况1:满足一边一锐角对应相等的两个直角三角形全等.
(1)
(2)
(3)
(AAS)
( ASA)
(AAS)
满足两直角边对应相等的两个直角三角形全等.
全等
( SAS)
情况;2
斜边和一条直角边对应相等的两个直角三角形.
判断:
满足下列条件的两直角三角形是否全等 为什么
动动手 做一做
用三角板和圆规,画一个Rt△ABC,使得∠C=90°,一直角边CA=4cm,斜边AB=5cm.
A
B
C
5cm
4cm
动动手 做一做
Step1:画∠MCN=90°;
C
N
M
动动手 做一做
Step1:画∠MCN=90°;
C
N
M
Step2:在射线CM上截取CA=4cm;
A
Step1:画∠MCN=90°;
Step2:在射线CM上截取CA=4cm;
动动手 做一做
Step3:以A为圆心,5cm为半径画弧,交射线CN于B;
C
N
M
A
B
Step1:画∠MCN=90°;
C
N
M
Step2:在射线CM上截取CA=4cm;
B
动动手 做一做
Step3:以A为圆心,5cm为半径画弧,交射线CN于B;
A
Step4:连结AB;
△ABC即为所要画的三角形
动动手 做一做 比比看
把我们刚画好的直角三角形剪下来,和同桌的比比看,
这些直角三角形有怎样的关系呢?
Rt△ABC≌
A
B
C
5cm
4cm
A′
B ′
C ′
5cm
4cm
斜边和一条直角边对应相等的两个直角三角形全等.
(简写成“斜边、直角边”
或“HL”)
说明:
1、只能用于证明直角三角形的全等。
hypotenuse 斜边 leg 直角边
2、SSS、SAS、ASA、AAS适用于任何三角形,
包括直角三角形。
例1
已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.
A
B
D
C
证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)
A
已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: BC=AD.
A
B
D
C
证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)
A
变式延伸
∴BC=AD.
小试牛刀
已知:AB=CD,AE⊥BC,DF⊥BC ,CE=BF,
求证:AE=DF
C
D
A
B
F
E
课堂小结
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
应用
“ SSS ”
已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形.
D
B
C
A
F
E
学以致用
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?
学以致用
先把它转化为一个纯数学问题:
已知:如图,AC=DF,AC⊥AB,DE⊥DF.
求证:∠ABC=∠DFE.
课后作业
作业本:
课本14页 练习:1
