1.1.3集合的基本运算示范教学课件(2)(16张PPT)
文档属性
| 名称 | 1.1.3集合的基本运算示范教学课件(2)(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 09:22:55 | ||
图片预览






文档简介
1.1.3 集合的基本运算
第2课时
新课导入
如果学校里所有同学组成的集合记为S,所有男同学组成的集合记为M,所有女同学组成的集合记为F,那么:
(1)?SF=M,?SM=F;(2)若x∈S且x?M,则x∈F.
(1)这三个集合之间有什么联系?
(2)如果x∈S且x?M,你能得到什么结论?
新知探究
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用U表示.如果集合A是全集U的一个子集,则由U中不属于A的所有元素组成的集合,称为A在U中的补集,记作?UA,读作“A在U中的补集”.由全集U及其子集A得到?UA,通常称为补集运算.
新知探究
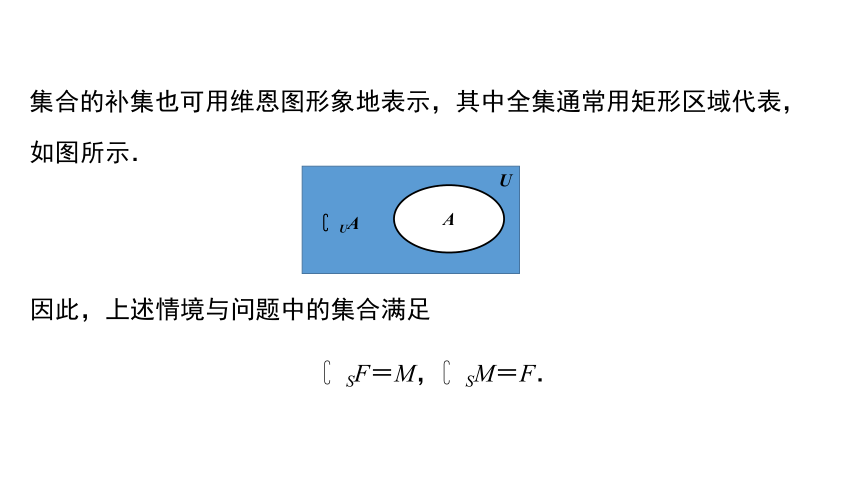
集合的补集也可用维恩图形象地表示,其中全集通常用矩形区域代表,
如图所示.
因此,上述情境与问题中的集合满足
?SF=M,?SM=F.
A
?UA
U
【练一练】(1)U={1,2,3,4,5,6},A={1,3,5},则?UA=________________
新知探究
(2)A=(-5,2],则?RA=_________________________
{2,4,6}
(-∞,-5]∪(2,+∞)
【想一想】在补集的定义中一共涉及几个集合?可以从哪些角度去研究这些集合?如何证明你的结论?
(1)A∪(?UA)=__________(2)A∩(?UA)=_________
(3)?U(?UA)=_______
新知探究
【做一做】(1)已知U={1,2,3},A={1},求?UA;
(2)已知U={1,2,3},?UA={1},求A;
(3)已知A={1},?UA={2,3},求U.
(1)?UA={2,3};
(2)A={2,3};
(3)U{1,2,3).
新知探究
【想一想】我们学习了交集、并集以及补集运算,那它们之间有什么关系呢?
如(?UA)∩(?UB),?U(A∪B),?U(A∩B),(?UA)∪(?UB)这几个集合之间有关系吗?
集合运算的德摩根恒等式?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
新知探究
例1 已知U={x∈N|x≤7},A={x∈U|x?≤7},B={x∈U|0<2x≤7},求?UA,?UB,(?UA)∪(?UB),?U(A∩B).
解:不难看出
U={0,1,2,3,4,5,6,7},A={0,1,2},B=(1,2,3}.
因此
?UA={3,4,5,6,7},
?UB={0,4,5,6,7},
(?UA)∪(?UB)={0,3,4,5,6,7},
?U(A∩B)={0,3,4,5,6,7}.
强调:注意U中的元素都是自然数,而且A,B都是U的子集.
新知探究
例2 已知A=(-1,+∞),B=(-∞,2],求?RA,?RB.
解:在数轴上表示出A和B,如图所示.
由图可知
?RA=(-∞,-1],?RB=(2,+∞).
新知探究
例3 已知全集U={1,3,x3+3x2+2x},A={1,|2x-1|},若?UA={0},求x的值.
解:∵?UA={0},∴0∈U,但0?A.
∴x3+3x2+2x=0,x(x+1)(x+2)=0,
∴x=0或-1或-2.
当x=0时,|2x-1|=1,A中已有元素1,不符合元素的互异性;
当x=-1时,|2x-1|=3,3∈U;
当x=-2时,|2x-1|=5,但5?U.
综上,x=-1.
归纳小结
回顾本节课,你有什么收获?
1.补集及其运算性质;
2.交集、并集与补集之间的关系.
作业:教科书第19页练习B 3,4题.
作业布置
第20页习题1-1A10题;
习题1-1 B 2题.
目标检测
设U为全集,对集合X,Y,定义运算“⊕”,满足X⊕Y=(?UX)∪Y,则对于任意集合X,Y,Z,则X⊕(Y⊕Z)=( )
1
D
根据运算“⊕”的定义可得,X⊕(Y⊕Z)=(?UX)∪[(?UY)]∪Z.
A.(X∪Y)∪(?UZ) B.(X∩Y)∪(?UZ)
C.[(?UX)∪(?UY)]∩Z D.(?UX)∪(?UY)]∪Z
目标检测
已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}且A??UB,求实数a的取值范围.
2
若B=?,则a+1>2a-1,∴a<2.
此时?UB=R,∴A??UB;
若B≠?,则a+1≤2a-1,即a≥2,
此时?UB={x|x<a+1,或x>2a-1},
由于A??UB,如图,
则a+1>5,∴a>4,
∴实数a的取值范围为a<2或a>4.
目标检测
已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}且A??UB,求实数a的取值范围.
2
易错点评:解决此类问题应注意以下几点:(1)空集作为特殊情况,不能忽略;(2)数形结合方法更加直观易懂,尽量使用;(3)端点值能否取到,应注意分析.
再见
第2课时
新课导入
如果学校里所有同学组成的集合记为S,所有男同学组成的集合记为M,所有女同学组成的集合记为F,那么:
(1)?SF=M,?SM=F;(2)若x∈S且x?M,则x∈F.
(1)这三个集合之间有什么联系?
(2)如果x∈S且x?M,你能得到什么结论?
新知探究
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用U表示.如果集合A是全集U的一个子集,则由U中不属于A的所有元素组成的集合,称为A在U中的补集,记作?UA,读作“A在U中的补集”.由全集U及其子集A得到?UA,通常称为补集运算.
新知探究
集合的补集也可用维恩图形象地表示,其中全集通常用矩形区域代表,
如图所示.
因此,上述情境与问题中的集合满足
?SF=M,?SM=F.
A
?UA
U
【练一练】(1)U={1,2,3,4,5,6},A={1,3,5},则?UA=________________
新知探究
(2)A=(-5,2],则?RA=_________________________
{2,4,6}
(-∞,-5]∪(2,+∞)
【想一想】在补集的定义中一共涉及几个集合?可以从哪些角度去研究这些集合?如何证明你的结论?
(1)A∪(?UA)=__________(2)A∩(?UA)=_________
(3)?U(?UA)=_______
新知探究
【做一做】(1)已知U={1,2,3},A={1},求?UA;
(2)已知U={1,2,3},?UA={1},求A;
(3)已知A={1},?UA={2,3},求U.
(1)?UA={2,3};
(2)A={2,3};
(3)U{1,2,3).
新知探究
【想一想】我们学习了交集、并集以及补集运算,那它们之间有什么关系呢?
如(?UA)∩(?UB),?U(A∪B),?U(A∩B),(?UA)∪(?UB)这几个集合之间有关系吗?
集合运算的德摩根恒等式?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
新知探究
例1 已知U={x∈N|x≤7},A={x∈U|x?≤7},B={x∈U|0<2x≤7},求?UA,?UB,(?UA)∪(?UB),?U(A∩B).
解:不难看出
U={0,1,2,3,4,5,6,7},A={0,1,2},B=(1,2,3}.
因此
?UA={3,4,5,6,7},
?UB={0,4,5,6,7},
(?UA)∪(?UB)={0,3,4,5,6,7},
?U(A∩B)={0,3,4,5,6,7}.
强调:注意U中的元素都是自然数,而且A,B都是U的子集.
新知探究
例2 已知A=(-1,+∞),B=(-∞,2],求?RA,?RB.
解:在数轴上表示出A和B,如图所示.
由图可知
?RA=(-∞,-1],?RB=(2,+∞).
新知探究
例3 已知全集U={1,3,x3+3x2+2x},A={1,|2x-1|},若?UA={0},求x的值.
解:∵?UA={0},∴0∈U,但0?A.
∴x3+3x2+2x=0,x(x+1)(x+2)=0,
∴x=0或-1或-2.
当x=0时,|2x-1|=1,A中已有元素1,不符合元素的互异性;
当x=-1时,|2x-1|=3,3∈U;
当x=-2时,|2x-1|=5,但5?U.
综上,x=-1.
归纳小结
回顾本节课,你有什么收获?
1.补集及其运算性质;
2.交集、并集与补集之间的关系.
作业:教科书第19页练习B 3,4题.
作业布置
第20页习题1-1A10题;
习题1-1 B 2题.
目标检测
设U为全集,对集合X,Y,定义运算“⊕”,满足X⊕Y=(?UX)∪Y,则对于任意集合X,Y,Z,则X⊕(Y⊕Z)=( )
1
D
根据运算“⊕”的定义可得,X⊕(Y⊕Z)=(?UX)∪[(?UY)]∪Z.
A.(X∪Y)∪(?UZ) B.(X∩Y)∪(?UZ)
C.[(?UX)∪(?UY)]∩Z D.(?UX)∪(?UY)]∪Z
目标检测
已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}且A??UB,求实数a的取值范围.
2
若B=?,则a+1>2a-1,∴a<2.
此时?UB=R,∴A??UB;
若B≠?,则a+1≤2a-1,即a≥2,
此时?UB={x|x<a+1,或x>2a-1},
由于A??UB,如图,
则a+1>5,∴a>4,
∴实数a的取值范围为a<2或a>4.
目标检测
已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}且A??UB,求实数a的取值范围.
2
易错点评:解决此类问题应注意以下几点:(1)空集作为特殊情况,不能忽略;(2)数形结合方法更加直观易懂,尽量使用;(3)端点值能否取到,应注意分析.
再见
