4.2 共点力平衡条件的应用课件20张PPT
文档属性
| 名称 | 4.2 共点力平衡条件的应用课件20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 601.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-04 13:22:11 | ||
图片预览







文档简介
共点力平衡条件的应用
知识与能力
1.知道什么是共点力作用下物体的平衡状态
2.掌握共点力的平衡条件
过程与方法
2.培养全面分析问题的能力和推理能力
1.培养应用力的矢量合成法则平行四边形定则进行力的合成、力的分解的能力
教学目标
3.会用共点力的平衡条件解决有关平衡问题
通过处理平衡问题培养学生养成具体问题具体分析的科学思维方式。
态度情感与价值观
1、共点力作用下物体的平衡状态。
2、共点力的平衡条件。
共点力的平衡条件
教学重难点
重点
难点
共点力作用下物体的平衡
一、平衡状态:
定义:一个物体在共点力的作用下,若保持静
止或匀速直线运动,则该物体处于平衡状态。
(1)静止:物体的______和_______都等
于零的状态.
速度
加速度
(2)匀速直线运动:物体的______不为零,
其________为零的状态.
速度
加速度
复习旧知
即:物体处于平衡状态,则加速度a一定等于0,所受合外力一定为零。
① 若处于平衡状态的物体仅受两个力作用,则这两个力一定大小相等、方向相反、作用在同一条直线上,即二力平衡.
② 若处于平衡状态的物体受三个力作用,则这三个力中的任意两个力的合力一定与第三个力大小相等、方向相反、作用在同一条直线上.
(力的合成)
③思考:若物体在三个以上的力的作用下而处于平衡状态呢?有什么特点?
答:物体受多个力作用处于平衡状态,其中任何一个力与其余力的合力大小相等方向相反.
二、平衡条件:
对物体受力分析,则物体所受合力为零,即F合=0
平衡问题的解题思路
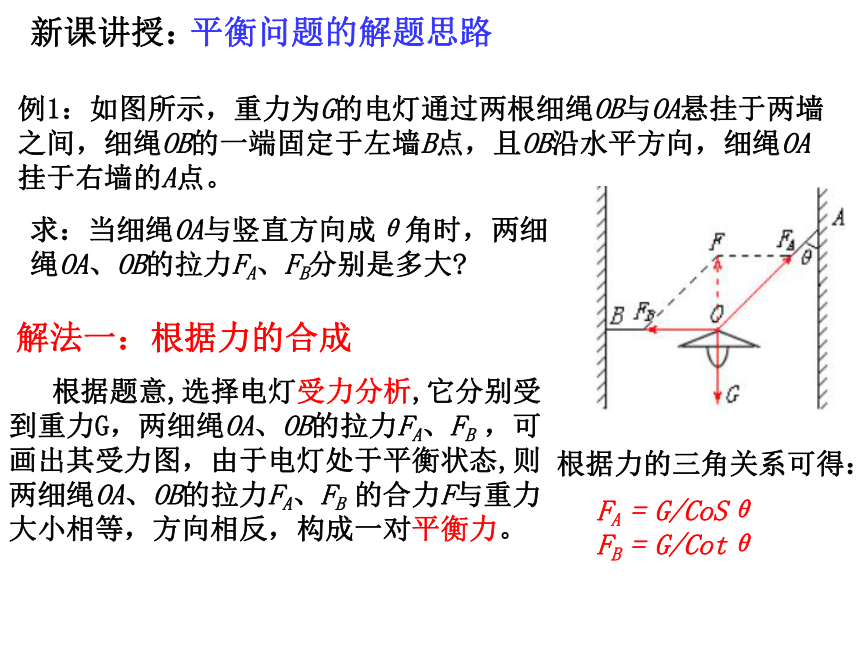
例1:如图所示,重力为G的电灯通过两根细绳OB与OA悬挂于两墙之间,细绳OB的一端固定于左墙B点,且OB沿水平方向,细绳OA挂于右墙的A点。
求:当细绳OA与竖直方向成θ角时,两细绳OA、OB的拉力FA、FB分别是多大?
解法一:根据力的合成
根据题意,选择电灯受力分析,它分别受到重力G,两细绳OA、OB的拉力FA、FB ,可画出其受力图,由于电灯处于平衡状态,则两细绳OA、OB的拉力FA、FB 的合力F与重力大小相等,方向相反,构成一对平衡力。
FA = G/CoSθ
FB = G/Cotθ
根据力的三角关系可得:
新课讲授:
解法二:根据力效果的分解
根据题意, 结点处受到电灯向下的拉力大小等于G,这个拉力产生了两个作用效果,方向如图所示,大小分别为F1,F2
T=G
F1
F2
F1=FA;F2=FB
FA
FB
由几何关系可得
F1=FA = G/CoSθ
F2=FB = G/Cotθ
解法三:正交分解
1、定义:把力按照两个选定的相互垂直的方向分解叫力的分解
2、步骤:
①选定研究对象,对研究对象进行受力分析
②建系
原点: (通常以力的作用点作为坐标原点)
坐标轴:(X、Y双轴------尽可能多的力落在坐标轴上)
③分解不在坐标轴上的力
④列方程
FX合=0
FY合=0
条件??
平衡!!!
三、正交分解
X
y
0
y
x
o
G
F1
F2
F1X
F1Y
F2Y
F2X
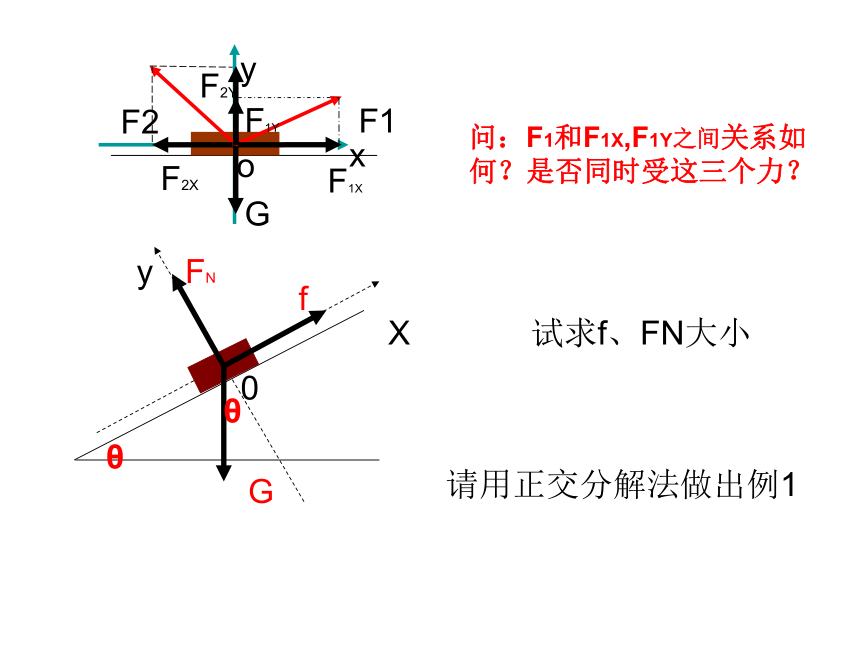
问:F1和F1X,F1Y之间关系如何?是否同时受这三个力?
θ
G
f
FN
θ
试求f、FN大小
请用正交分解法做出例1
平衡问题的解题思路
例2:如图所示,重力为G的电灯通过两根细绳OB与OA悬挂于两墙之间,细绳OB的一端固定于左墙B点,且OB沿水平方向,细绳OA挂于右墙的A点。
求:①当细绳OA与竖直方向成θ角时,两细绳OA、OB的拉力FA、FB分别是多大?
FA = G/CoSθ
FB = G/Cotθ
动态平衡的解题思路
何谓动态平衡?
物体在多个力作用下处于平衡状态,其中部分力发生变化,但物体始终处于受力平衡的状态。
例3:如图所示.挡板AB和竖直墙之间夹有小球,球的质量为m,则挡板与竖直墙壁之间的夹角θ缓慢增加至θ=90°时,AB板及墙对球压力如何变化?
关键字眼:缓慢、逐渐变化
思路一:试一下解析法是否可行
点评:可以通过正交分解写出各个力的表达式,借助表达式中θ的变化分析各个力变化的情况。
思路二:图解法
物体受三个力作用:重力G,垂直于墙的弹力N1和垂直于挡板的弹力N2的作用,当挡板与竖直墙壁之间的夹角θ缓慢增加时物体可以看做处于一系列的动态平衡状态.即任意两个力的合力一定始终与第三个力等大反向,且构成矢量三角形。
N1’’
重力大小方向均未发生变化(将其反向可看作另外两个力的合力),在整个变化过程中,可看作两个拉力的合力大小始终为G,方向始终竖直向上,且其中一个分力(N1)方向也始终不变,大小随着F2的变化而变化,则构成的动态的矢量三角形如图。
N1’
N2’
N2,,
整个变化过程中,由平衡条件知,两个弹力的合力N大小方向都不变(等于G),与向下的重力等大反向.据此可知作出几组平行四边形,反映出N1、N2的变化情况,如上图所示.当θ逐渐增大时,N2与竖直方向的夹角逐渐减小,N2→N′2→N″2;当θ=90°时,N2=N=G=mg,所以N2逐渐减小,N1逐渐减小.
(1)解析法:进行受力分析后建立平衡方程,求出应变参量与自变参量的一般函数式,然后根据自变量的变化确定应变参量的变化.
(2)图解法:进行受力分析后,再根据平行四边形定则或三角形定则画出不同状态下的力的矢量图(画在同一个图中),然后根据有向线段(表示力)的长度变化判断各个力的变化情况.
图解法适用条件:
质点在三个力作用下处于平衡状态,其中一个力恒定,一个力的方向不变,第三个力的大小和方向都变化的情况.具体做法是:合成两个变力,其合力与恒力等值反向.
动态平衡问题的分析方法:
思考题:
如图示半径为r,表面光滑的半球体被固定在水平地面上,跨过无摩擦的定滑轮,用一根轻绳下挂一个质量为m的小球,将小球置于半球体光滑的表面上,并使定滑轮位于半球体的正上方,现用力F斜左向下拉绳的自由端,使小球沿光滑半球面缓慢向上滑动。在此过程中,半球体对小球的支持力FN 和绳子的拉力F的变此情况。
则小球沿光滑半球面缓慢向上滑动过程中,半球体对小球的支持力FN 不变,绳子的拉力F不断减小。
分析与解:
根据平衡的特点,由力的几何结构可知:
即
补充:三角形相似法
小结:
解这种题型首先对动态平衡的物体受力分析,确定三个力的特点;找出不变力,则另两个变力的合力就与该不变力构成一对平衡力,用力的合成分解法、图解法或力的矢量三角形与结构三角形相似法解决。
求解共点力体用下平衡问题的解题一般步骤:
1)确定研究对象(物体或结点);
2)对研究对象进行受力分析,并画受力图;
3)分析判断研究对象是否处于平衡状态;
4)根据物体的受力和己知条件,运用共点力平衡条
件,选用适当方法计算求解。
当堂巩固
1. 如图所示,物体B的上表面水平,B上面载着物体A,当它们一起沿固定斜面C匀速下滑的过程中物体A受力是( )
A、只受重力
B、只受重力和支持力
C、有重力、支持力和摩擦力
D、有重力、支持力、摩擦力和斜面对它的弹力
A
B
C
B
2. 在力的合成中,下列关于两个分力(大小为定值)与它们的合力的关系的说法中,正确的是( )
A、合力一定大于每一个分力;
B、合力一定小于分力;
C、合力的方向一定与分力的方向相同;
D、两个分力的夹角在0°~180°变化时,夹角越大合力越小
D
3. 物体A、B、C叠放在水平桌面上,用水平力F拉B,使三者一起匀速向右运动,则( )
A、物体A对物体B有向左的摩擦力作用;
B、物体B对物体C有向右的摩擦力作用;
C、桌面对物体A有向左的摩擦力作用;
D、桌面和物体A之间没有摩擦力的作用
A
B
C
F
AC
谢谢
知识与能力
1.知道什么是共点力作用下物体的平衡状态
2.掌握共点力的平衡条件
过程与方法
2.培养全面分析问题的能力和推理能力
1.培养应用力的矢量合成法则平行四边形定则进行力的合成、力的分解的能力
教学目标
3.会用共点力的平衡条件解决有关平衡问题
通过处理平衡问题培养学生养成具体问题具体分析的科学思维方式。
态度情感与价值观
1、共点力作用下物体的平衡状态。
2、共点力的平衡条件。
共点力的平衡条件
教学重难点
重点
难点
共点力作用下物体的平衡
一、平衡状态:
定义:一个物体在共点力的作用下,若保持静
止或匀速直线运动,则该物体处于平衡状态。
(1)静止:物体的______和_______都等
于零的状态.
速度
加速度
(2)匀速直线运动:物体的______不为零,
其________为零的状态.
速度
加速度
复习旧知
即:物体处于平衡状态,则加速度a一定等于0,所受合外力一定为零。
① 若处于平衡状态的物体仅受两个力作用,则这两个力一定大小相等、方向相反、作用在同一条直线上,即二力平衡.
② 若处于平衡状态的物体受三个力作用,则这三个力中的任意两个力的合力一定与第三个力大小相等、方向相反、作用在同一条直线上.
(力的合成)
③思考:若物体在三个以上的力的作用下而处于平衡状态呢?有什么特点?
答:物体受多个力作用处于平衡状态,其中任何一个力与其余力的合力大小相等方向相反.
二、平衡条件:
对物体受力分析,则物体所受合力为零,即F合=0
平衡问题的解题思路
例1:如图所示,重力为G的电灯通过两根细绳OB与OA悬挂于两墙之间,细绳OB的一端固定于左墙B点,且OB沿水平方向,细绳OA挂于右墙的A点。
求:当细绳OA与竖直方向成θ角时,两细绳OA、OB的拉力FA、FB分别是多大?
解法一:根据力的合成
根据题意,选择电灯受力分析,它分别受到重力G,两细绳OA、OB的拉力FA、FB ,可画出其受力图,由于电灯处于平衡状态,则两细绳OA、OB的拉力FA、FB 的合力F与重力大小相等,方向相反,构成一对平衡力。
FA = G/CoSθ
FB = G/Cotθ
根据力的三角关系可得:
新课讲授:
解法二:根据力效果的分解
根据题意, 结点处受到电灯向下的拉力大小等于G,这个拉力产生了两个作用效果,方向如图所示,大小分别为F1,F2
T=G
F1
F2
F1=FA;F2=FB
FA
FB
由几何关系可得
F1=FA = G/CoSθ
F2=FB = G/Cotθ
解法三:正交分解
1、定义:把力按照两个选定的相互垂直的方向分解叫力的分解
2、步骤:
①选定研究对象,对研究对象进行受力分析
②建系
原点: (通常以力的作用点作为坐标原点)
坐标轴:(X、Y双轴------尽可能多的力落在坐标轴上)
③分解不在坐标轴上的力
④列方程
FX合=0
FY合=0
条件??
平衡!!!
三、正交分解
X
y
0
y
x
o
G
F1
F2
F1X
F1Y
F2Y
F2X
问:F1和F1X,F1Y之间关系如何?是否同时受这三个力?
θ
G
f
FN
θ
试求f、FN大小
请用正交分解法做出例1
平衡问题的解题思路
例2:如图所示,重力为G的电灯通过两根细绳OB与OA悬挂于两墙之间,细绳OB的一端固定于左墙B点,且OB沿水平方向,细绳OA挂于右墙的A点。
求:①当细绳OA与竖直方向成θ角时,两细绳OA、OB的拉力FA、FB分别是多大?
FA = G/CoSθ
FB = G/Cotθ
动态平衡的解题思路
何谓动态平衡?
物体在多个力作用下处于平衡状态,其中部分力发生变化,但物体始终处于受力平衡的状态。
例3:如图所示.挡板AB和竖直墙之间夹有小球,球的质量为m,则挡板与竖直墙壁之间的夹角θ缓慢增加至θ=90°时,AB板及墙对球压力如何变化?
关键字眼:缓慢、逐渐变化
思路一:试一下解析法是否可行
点评:可以通过正交分解写出各个力的表达式,借助表达式中θ的变化分析各个力变化的情况。
思路二:图解法
物体受三个力作用:重力G,垂直于墙的弹力N1和垂直于挡板的弹力N2的作用,当挡板与竖直墙壁之间的夹角θ缓慢增加时物体可以看做处于一系列的动态平衡状态.即任意两个力的合力一定始终与第三个力等大反向,且构成矢量三角形。
N1’’
重力大小方向均未发生变化(将其反向可看作另外两个力的合力),在整个变化过程中,可看作两个拉力的合力大小始终为G,方向始终竖直向上,且其中一个分力(N1)方向也始终不变,大小随着F2的变化而变化,则构成的动态的矢量三角形如图。
N1’
N2’
N2,,
整个变化过程中,由平衡条件知,两个弹力的合力N大小方向都不变(等于G),与向下的重力等大反向.据此可知作出几组平行四边形,反映出N1、N2的变化情况,如上图所示.当θ逐渐增大时,N2与竖直方向的夹角逐渐减小,N2→N′2→N″2;当θ=90°时,N2=N=G=mg,所以N2逐渐减小,N1逐渐减小.
(1)解析法:进行受力分析后建立平衡方程,求出应变参量与自变参量的一般函数式,然后根据自变量的变化确定应变参量的变化.
(2)图解法:进行受力分析后,再根据平行四边形定则或三角形定则画出不同状态下的力的矢量图(画在同一个图中),然后根据有向线段(表示力)的长度变化判断各个力的变化情况.
图解法适用条件:
质点在三个力作用下处于平衡状态,其中一个力恒定,一个力的方向不变,第三个力的大小和方向都变化的情况.具体做法是:合成两个变力,其合力与恒力等值反向.
动态平衡问题的分析方法:
思考题:
如图示半径为r,表面光滑的半球体被固定在水平地面上,跨过无摩擦的定滑轮,用一根轻绳下挂一个质量为m的小球,将小球置于半球体光滑的表面上,并使定滑轮位于半球体的正上方,现用力F斜左向下拉绳的自由端,使小球沿光滑半球面缓慢向上滑动。在此过程中,半球体对小球的支持力FN 和绳子的拉力F的变此情况。
则小球沿光滑半球面缓慢向上滑动过程中,半球体对小球的支持力FN 不变,绳子的拉力F不断减小。
分析与解:
根据平衡的特点,由力的几何结构可知:
即
补充:三角形相似法
小结:
解这种题型首先对动态平衡的物体受力分析,确定三个力的特点;找出不变力,则另两个变力的合力就与该不变力构成一对平衡力,用力的合成分解法、图解法或力的矢量三角形与结构三角形相似法解决。
求解共点力体用下平衡问题的解题一般步骤:
1)确定研究对象(物体或结点);
2)对研究对象进行受力分析,并画受力图;
3)分析判断研究对象是否处于平衡状态;
4)根据物体的受力和己知条件,运用共点力平衡条
件,选用适当方法计算求解。
当堂巩固
1. 如图所示,物体B的上表面水平,B上面载着物体A,当它们一起沿固定斜面C匀速下滑的过程中物体A受力是( )
A、只受重力
B、只受重力和支持力
C、有重力、支持力和摩擦力
D、有重力、支持力、摩擦力和斜面对它的弹力
A
B
C
B
2. 在力的合成中,下列关于两个分力(大小为定值)与它们的合力的关系的说法中,正确的是( )
A、合力一定大于每一个分力;
B、合力一定小于分力;
C、合力的方向一定与分力的方向相同;
D、两个分力的夹角在0°~180°变化时,夹角越大合力越小
D
3. 物体A、B、C叠放在水平桌面上,用水平力F拉B,使三者一起匀速向右运动,则( )
A、物体A对物体B有向左的摩擦力作用;
B、物体B对物体C有向右的摩擦力作用;
C、桌面对物体A有向左的摩擦力作用;
D、桌面和物体A之间没有摩擦力的作用
A
B
C
F
AC
谢谢
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
