三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大)沪教版
文档属性
| 名称 | 三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大)沪教版 |  | |
| 格式 | docx | ||
| 文件大小 | 32.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 13:08:52 | ||
图片预览


文档简介
《谁围出的面积最大》教学设计
教学内容
谁围出的面积最大
课型
新授课
课时
第一课时
教
学
状
态
分
析
教材分析:
《谁围出的面积最大》是三年级第二学期第七单元《整理与提高》数学广场中的一个内容。教材安排的内容是“用火柴棒围图形”,它是课本第64页探究的继续,即探究“在长方形周长不变的前提下,长和宽何种关系时图形面积最大”。这一内容比以前更进了一步,其巧妙之处在于将动手与动脑结合在一起,教师在组织教学时放手让学生自己探究。因为要最终得出答案,对于此阶段的学生只能通过对每一种可能的情况进行计算分析后得出。
学情分析:
1.学生在二年级时学习过“长方形和正方形”,知道它们的特征,上学期又学习了“长方形和正方形的面积”,知道了这两种图形的计算方法,也知道了多边形的特点,这学期第六单元也学习过长方形、正方形的周长。因此对于今天所学的内容,学生已先期具备了一定的知识基础的。
2.在日常的学习中学生已经养成了自主探究的习惯,能在教师提供的背景条件下,自己观察、分析探究出结论来。因此对于今天所学的知识,学生也是具有一定的能力基础的。
教学目标:
1.通过围出长方形(包括正方形)的具体操作,探究“长方形周长相等时,长宽差变化与面积变化之间的关系”。
2.通过对所围长方形进行观察、验证等活动,经历探究问题的全过程,初步掌握探究问题的方法,并获得成功的体验。
3.在探究活动中,渗透有序思维、数形结合的数学思想。
教学重难点:
重点:探究长方形周长相等时,长宽差与面积之间的关系。
难点:发现长方形周长一定,当长宽差最小时,面积最大。
教学准备:学习单、多媒体课件、火柴
教学
板块
目标指向
师生活动
评价关注点
一.
提出问题,游戏引入
以算式(数的)形式,为探究“长、宽与面积之间的关系”作铺垫,初步感受数形结合的思想。
出示问题:
●+■= 16,●×■的积最大是()
生:48,64.....
师:那到底是多少呢?老师先不揭晓答案,我们先一起来玩个火柴游戏,从这个游戏中你们一定会找到答案的。
说出●×■积的情况。
二、
深入探究,发现规律
让学生动手围图形,初次感悟“周长相等,面积不一定相等”。
验证“周长相等,面积不一定相等”。
发现围成的长方形“周长相等时,长宽差越小,面积越大”。
验证:周长相等时,长宽差越小,面积越大。
发现“周长相等时,长宽差为0时,面积最大”。
再次验证“周长相等时,长宽差越小,面积越大”
用长方形长、宽与面积之间关系的规律,解决问题,渗透数形结合思想。
第一关:8根火柴
师:请同学们用8根火柴围出一个学过的图形。
学生尝试围图形
交流所围图形。
师:你们围的图形什么是相等的?
生:周长相等。
师:那面积相等吗?
生:不相等。
得出:周长相等,面积不一定相等。
师:正八边形、三角形的面积到了以后会学习,这节课我们主要探究长方形、正方形的面积,谁围出的面积最大(板书)
继续进行火柴游戏
第二关:14根火柴
师:你能用14根火柴围出几种长方形?1人摆,1人完成学习单记录。
为方便记录,把每一根火柴记作单位1
周长
长宽和
长
宽
长宽差
面积
14
7
6
1
5
6
5
2
3
10
4
3
1
12
在对比学生记录表格中渗透有序的数学思想。
师:仔细观察表格中的长宽差的变化和面积的变化,有什么关系呢?
生:长宽差越小,面积越大。
得出发现:长宽差越小,面积越大。
师:这种发现是偶然现象,还是存在必然联系呢?
需要我们继续来围图形验证一下。
师:再加1根火柴,现在15根火柴可以围长方形吗?
生:不可以。15不能被2整除。
师:说的真棒。
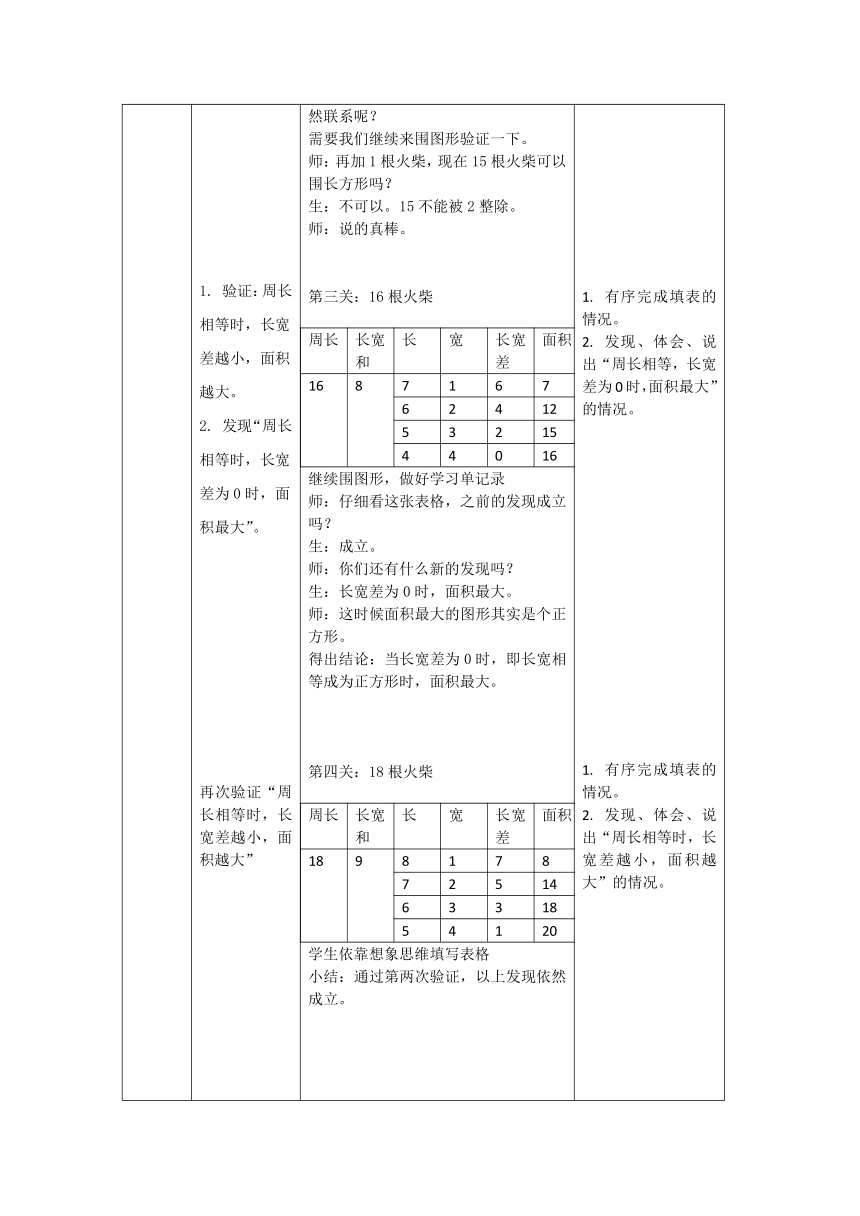
第三关:16根火柴
继续围图形,做好学习单记录
周长
长宽和
长
宽
长宽差
面积
16
8
7
1
6
7
6
2
4
12
5
3
2
15
4
4
0
16
师:仔细看这张表格,之前的发现成立吗?
生:成立。
师:你们还有什么新的发现吗?
生:长宽差为0时,面积最大。
师:这时候面积最大的图形其实是个正方形。
得出结论:当长宽差为0时,即长宽相等成为正方形时,面积最大。
第四关:18根火柴
学生依靠想象思维填写表格
周长
长宽和
长
宽
长宽差
面积
18
9
8
1
7
8
7
2
5
14
6
3
3
18
5
4
1
20
小结:通过第两次验证,以上发现依然成立。
火柴游戏到这就结束了,我们也收获了其中的秘密。再回过头来看这道题目,你能解决了吗?
●+■= 16,●×■的积最大是()
生:8×8=64
生:●也就是长,■是宽,●+■= 16是长宽和,●×■的积最大也就是面积最大,所以当长是8,宽是8的长方形(正方形)面积最大。
师:真棒,你竟然从游戏中获取了解决问题的方法。
师:请同学们一定要牢记这个结论,它能够帮助我们解决生活中的很多问题。
1.积极参与小组探究。
2.围成不同图形的情况。
3.体会周长相等,面积不一定相等。
按要求填表的情况。
发现、体会、说出“长方形周长相等时,长宽差越小,面积越大”的情况。
有序完成填表的情况。
发现、体会、说出“周长相等,长宽差为0时,面积最大”的情况。
有序完成填表的情况。
发现、体会、说出“周长相等时,长宽差越小,面积越大”的情况。
迁移、联系、说出“两个式子与长宽和、面积”之间联系的情况。
三、
练习
巩固
内化
提升
运用“长方形周长相等时,长、宽与面积之间的关系”,解决实际生活问题,并获得成功的体验。
1936751111251.
长方形周长是26厘米(长宽取整厘米数),长宽和是(),当长是(),宽是(),面积最大,面积是()。
农场里原来用绳子围一个长15米,宽5米的长方形停车场,现在既不想增加绳子的长度,又想扩大停车场的面积,那么停车场的面积最大可以是()平方米?
小小设计师
学校的空地上要用14根铁栅栏设计一个面积最大的长方形花坛,(请你先用简图画一画),已知每一根铁栅栏是5米,此时的面积最大是多少?
独立正确答题的情况。
四、
总结
深化
回忆整节课的学习内容
完成数学日记
1.长方形周长相等,面积 )相等。
2.长方形周长相等,长宽差越小,面积( )。长宽差为( )时,即长宽相等成为( )形时,面积最大。
学生能主动发言,回忆出课堂学习内容。
五.作业布置
练习巩固
练习卷
六.板书设计:
谁围出的面积最大——长方形、正方形
周长相等 1. 面积不一定相等
2. 长宽差越小,面积越大;
(长宽差为0时,面积最大)
正方形
七.教学反思:
《谁围出的面积最大》学习单
姓名:
周长
长宽和
长
宽
长宽差
面积
一.火柴游戏
14根火柴:
我发现:周长相等,长宽差越( ),面积越( )。
周长
长宽和
长
宽
长宽差
面积
16根火柴:
我发现:周长相等,长宽差为0时,即长宽相等成为( )形时,面积( )。
18根火柴:
周长
长宽和
长
宽
长宽差
面积
二.应用
228600711201.
长方形周长是26厘米(长宽取整厘米),长宽和是( )厘米,当长是( )厘米,宽是( )厘米时,面积最大,且面积是( )。
2. 农场里原来用绳子围一个长15米,宽5米的长方形停车场,现在既不想增加绳子的长度,又想扩大停车场的面积,那么停车场的面积最大可以是多少平方米?
数学日记
1.长方形周长相等,面积( )相等。
2.长方形周长相等,长宽差越小,面积( )。
长宽差为( )时,即长宽相等成为( )形时,面积最大。
评
价
单
自评
师评
学习成果
学习习惯
学习兴趣
优()
良()
合格()
需努力()
甲()
乙()
丙()
☆()
△()
3. 学校的空地上要用14根铁栅栏围一个面积最大的长方形花坛,(请你先用简图画一画),已知每一根铁栅栏是5米,此时的面积最大是多少?
教学内容
谁围出的面积最大
课型
新授课
课时
第一课时
教
学
状
态
分
析
教材分析:
《谁围出的面积最大》是三年级第二学期第七单元《整理与提高》数学广场中的一个内容。教材安排的内容是“用火柴棒围图形”,它是课本第64页探究的继续,即探究“在长方形周长不变的前提下,长和宽何种关系时图形面积最大”。这一内容比以前更进了一步,其巧妙之处在于将动手与动脑结合在一起,教师在组织教学时放手让学生自己探究。因为要最终得出答案,对于此阶段的学生只能通过对每一种可能的情况进行计算分析后得出。
学情分析:
1.学生在二年级时学习过“长方形和正方形”,知道它们的特征,上学期又学习了“长方形和正方形的面积”,知道了这两种图形的计算方法,也知道了多边形的特点,这学期第六单元也学习过长方形、正方形的周长。因此对于今天所学的内容,学生已先期具备了一定的知识基础的。
2.在日常的学习中学生已经养成了自主探究的习惯,能在教师提供的背景条件下,自己观察、分析探究出结论来。因此对于今天所学的知识,学生也是具有一定的能力基础的。
教学目标:
1.通过围出长方形(包括正方形)的具体操作,探究“长方形周长相等时,长宽差变化与面积变化之间的关系”。
2.通过对所围长方形进行观察、验证等活动,经历探究问题的全过程,初步掌握探究问题的方法,并获得成功的体验。
3.在探究活动中,渗透有序思维、数形结合的数学思想。
教学重难点:
重点:探究长方形周长相等时,长宽差与面积之间的关系。
难点:发现长方形周长一定,当长宽差最小时,面积最大。
教学准备:学习单、多媒体课件、火柴
教学
板块
目标指向
师生活动
评价关注点
一.
提出问题,游戏引入
以算式(数的)形式,为探究“长、宽与面积之间的关系”作铺垫,初步感受数形结合的思想。
出示问题:
●+■= 16,●×■的积最大是()
生:48,64.....
师:那到底是多少呢?老师先不揭晓答案,我们先一起来玩个火柴游戏,从这个游戏中你们一定会找到答案的。
说出●×■积的情况。
二、
深入探究,发现规律
让学生动手围图形,初次感悟“周长相等,面积不一定相等”。
验证“周长相等,面积不一定相等”。
发现围成的长方形“周长相等时,长宽差越小,面积越大”。
验证:周长相等时,长宽差越小,面积越大。
发现“周长相等时,长宽差为0时,面积最大”。
再次验证“周长相等时,长宽差越小,面积越大”
用长方形长、宽与面积之间关系的规律,解决问题,渗透数形结合思想。
第一关:8根火柴
师:请同学们用8根火柴围出一个学过的图形。
学生尝试围图形
交流所围图形。
师:你们围的图形什么是相等的?
生:周长相等。
师:那面积相等吗?
生:不相等。
得出:周长相等,面积不一定相等。
师:正八边形、三角形的面积到了以后会学习,这节课我们主要探究长方形、正方形的面积,谁围出的面积最大(板书)
继续进行火柴游戏
第二关:14根火柴
师:你能用14根火柴围出几种长方形?1人摆,1人完成学习单记录。
为方便记录,把每一根火柴记作单位1
周长
长宽和
长
宽
长宽差
面积
14
7
6
1
5
6
5
2
3
10
4
3
1
12
在对比学生记录表格中渗透有序的数学思想。
师:仔细观察表格中的长宽差的变化和面积的变化,有什么关系呢?
生:长宽差越小,面积越大。
得出发现:长宽差越小,面积越大。
师:这种发现是偶然现象,还是存在必然联系呢?
需要我们继续来围图形验证一下。
师:再加1根火柴,现在15根火柴可以围长方形吗?
生:不可以。15不能被2整除。
师:说的真棒。
第三关:16根火柴
继续围图形,做好学习单记录
周长
长宽和
长
宽
长宽差
面积
16
8
7
1
6
7
6
2
4
12
5
3
2
15
4
4
0
16
师:仔细看这张表格,之前的发现成立吗?
生:成立。
师:你们还有什么新的发现吗?
生:长宽差为0时,面积最大。
师:这时候面积最大的图形其实是个正方形。
得出结论:当长宽差为0时,即长宽相等成为正方形时,面积最大。
第四关:18根火柴
学生依靠想象思维填写表格
周长
长宽和
长
宽
长宽差
面积
18
9
8
1
7
8
7
2
5
14
6
3
3
18
5
4
1
20
小结:通过第两次验证,以上发现依然成立。
火柴游戏到这就结束了,我们也收获了其中的秘密。再回过头来看这道题目,你能解决了吗?
●+■= 16,●×■的积最大是()
生:8×8=64
生:●也就是长,■是宽,●+■= 16是长宽和,●×■的积最大也就是面积最大,所以当长是8,宽是8的长方形(正方形)面积最大。
师:真棒,你竟然从游戏中获取了解决问题的方法。
师:请同学们一定要牢记这个结论,它能够帮助我们解决生活中的很多问题。
1.积极参与小组探究。
2.围成不同图形的情况。
3.体会周长相等,面积不一定相等。
按要求填表的情况。
发现、体会、说出“长方形周长相等时,长宽差越小,面积越大”的情况。
有序完成填表的情况。
发现、体会、说出“周长相等,长宽差为0时,面积最大”的情况。
有序完成填表的情况。
发现、体会、说出“周长相等时,长宽差越小,面积越大”的情况。
迁移、联系、说出“两个式子与长宽和、面积”之间联系的情况。
三、
练习
巩固
内化
提升
运用“长方形周长相等时,长、宽与面积之间的关系”,解决实际生活问题,并获得成功的体验。
1936751111251.
长方形周长是26厘米(长宽取整厘米数),长宽和是(),当长是(),宽是(),面积最大,面积是()。
农场里原来用绳子围一个长15米,宽5米的长方形停车场,现在既不想增加绳子的长度,又想扩大停车场的面积,那么停车场的面积最大可以是()平方米?
小小设计师
学校的空地上要用14根铁栅栏设计一个面积最大的长方形花坛,(请你先用简图画一画),已知每一根铁栅栏是5米,此时的面积最大是多少?
独立正确答题的情况。
四、
总结
深化
回忆整节课的学习内容
完成数学日记
1.长方形周长相等,面积 )相等。
2.长方形周长相等,长宽差越小,面积( )。长宽差为( )时,即长宽相等成为( )形时,面积最大。
学生能主动发言,回忆出课堂学习内容。
五.作业布置
练习巩固
练习卷
六.板书设计:
谁围出的面积最大——长方形、正方形
周长相等 1. 面积不一定相等
2. 长宽差越小,面积越大;
(长宽差为0时,面积最大)
正方形
七.教学反思:
《谁围出的面积最大》学习单
姓名:
周长
长宽和
长
宽
长宽差
面积
一.火柴游戏
14根火柴:
我发现:周长相等,长宽差越( ),面积越( )。
周长
长宽和
长
宽
长宽差
面积
16根火柴:
我发现:周长相等,长宽差为0时,即长宽相等成为( )形时,面积( )。
18根火柴:
周长
长宽和
长
宽
长宽差
面积
二.应用
228600711201.
长方形周长是26厘米(长宽取整厘米),长宽和是( )厘米,当长是( )厘米,宽是( )厘米时,面积最大,且面积是( )。
2. 农场里原来用绳子围一个长15米,宽5米的长方形停车场,现在既不想增加绳子的长度,又想扩大停车场的面积,那么停车场的面积最大可以是多少平方米?
数学日记
1.长方形周长相等,面积( )相等。
2.长方形周长相等,长宽差越小,面积( )。
长宽差为( )时,即长宽相等成为( )形时,面积最大。
评
价
单
自评
师评
学习成果
学习习惯
学习兴趣
优()
良()
合格()
需努力()
甲()
乙()
丙()
☆()
△()
3. 学校的空地上要用14根铁栅栏围一个面积最大的长方形花坛,(请你先用简图画一画),已知每一根铁栅栏是5米,此时的面积最大是多少?
