2020年秋人教版九年级数学上册随堂练23.2.1中心对称学情练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练23.2.1中心对称学情练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 13:10:33 | ||
图片预览



文档简介
23.2.1中心对称学情练习
一、选择题
1.
剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,如图所示的剪纸图案( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
2.
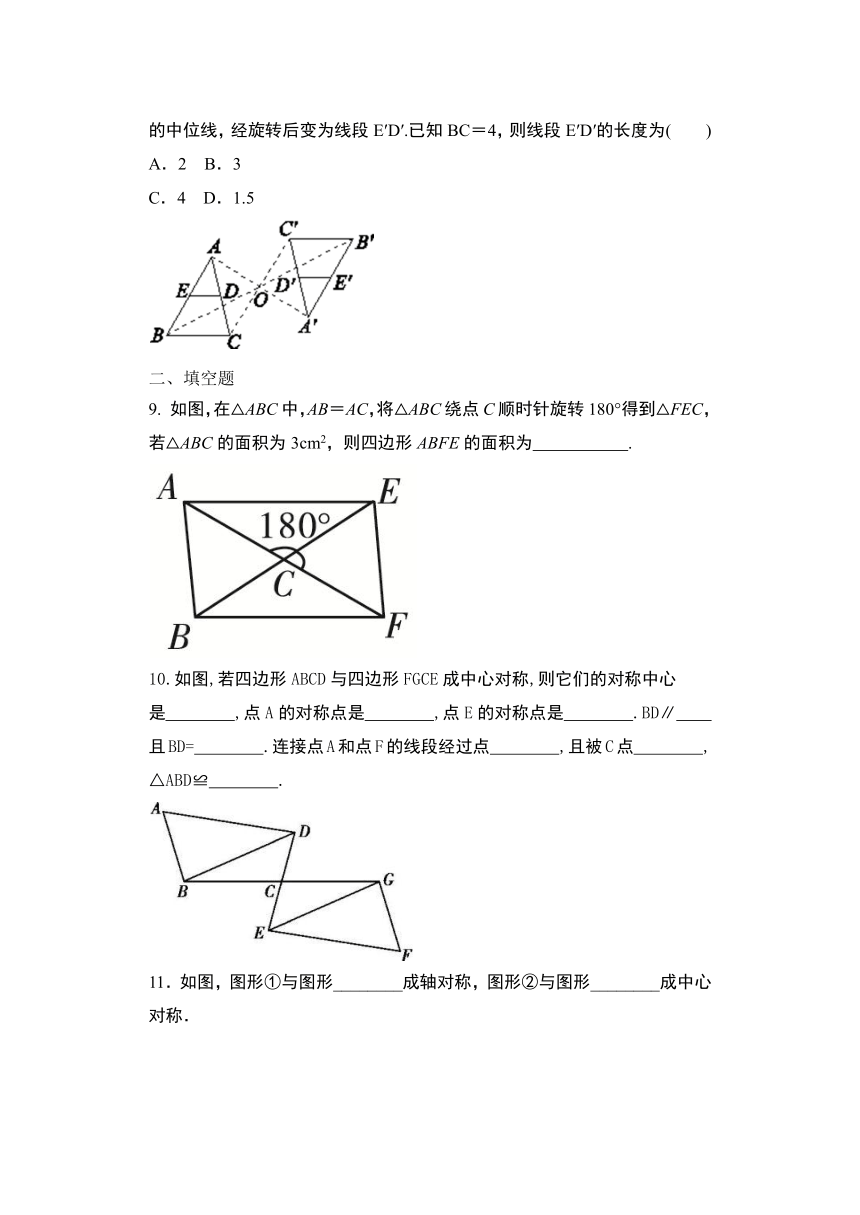
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.
2
B.
3
C.
4
D.
1.5
3.如图,平行四边形ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有(
)
A.4对
B.3对
C.2对
D.1对
4.点A和点B的坐标分别为(0,2),(1,0),若将△OAB绕点B顺时针旋转180°后,得到△OAB,则点A的对应点A的坐标是( )
A.(0,2)
B.(2,2)
C.(-2,2) D.(2,-2)
5.
如图所示的四组图形中,左边的图形与右边的图形成中心对称的是( )
A
B
C
D
6.如图,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是(
)
A.AB=A′B′,BC=B′C′
B.AB∥A′B′,BC∥B′C′
C.S△ABC=S△A′B′C′
D.△ABC≌△A′OC′
7.
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为( )
A.4 B.12
C.6 D.3
8.
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2
B.3
C.4
D.1.5
二、填空题
9.
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转180°得到△FEC,若△ABC的面积为3cm2,则四边形ABFE的面积为
.
10.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 .BD∥ 且BD= .连接点A和点F的线段经过点 ,且被C点 ,△ABD≌ .?
11.如图,图形①与图形________成轴对称,图形②与图形________成中心对称.
12.如图,已知AB=3,AC=1,∠D=90°,△DEC
与△ABC关于点C成中心对称,点F是DE的中点,连接CF,则CF的长是 .?
13.如图,已知△ABC与△ADE关于点A成中心对称,若AB=2
cm,那么BD的长为________.
14.
如图,点O是?ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=0.5AB;G,H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是_________.
三、解答题
15.
如图所示,已知△ABC外一点O,画△A′B′C′,使△A′B′C′与△ABC关于O点中心对称.
16.
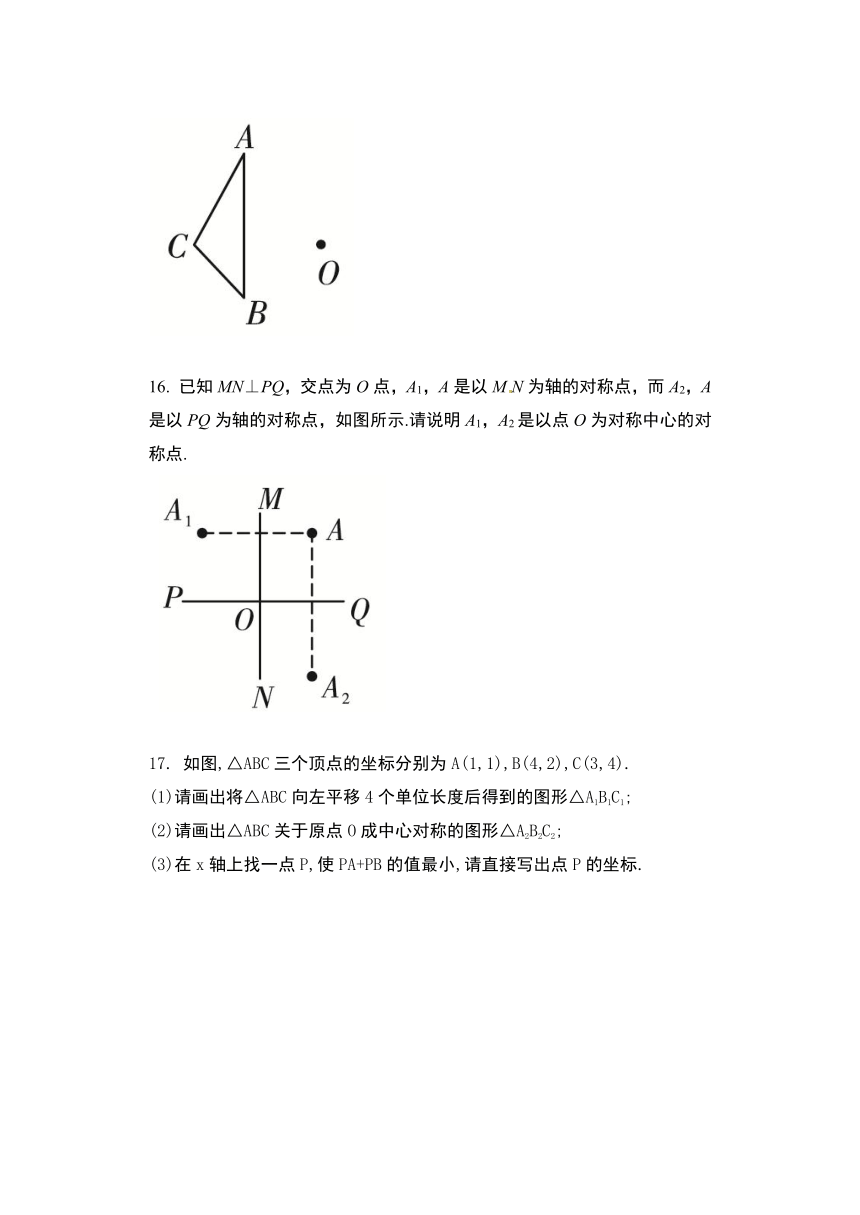
已知MN⊥PQ,交点为O点,A1,A是以MN为轴的对称点,而A2,A是以PQ为轴的对称点,如图所示.请说明A1,A2是以点O为对称中心的对称点.
17.
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
18.
如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O对称.求证:BF=DE.
19.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
20.△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A?B?C;
(2)写出点A?、B?的坐标.
21.
如图
,在△ABC中,点O是AC
的中点,△CDA与△ABC关于点O中心对称,若AB=6,∠BAC=
40?,则CD的长度是多少,∠ACD的度数是多少.
答案
1.
B
2.
A
3.
A
4.
D
5.
A
6.
D
7.
D
8.
A
9.
12cm2
10.
C;F;D;EG;EG;C;平分;△FGE
11.
④,③
12.
13.
4cm
14.
=
15.
解:如图所示.
16.
证明:如图所示,连接AA1,AA2,OA,OA1,OA2,∵A,A1是以MN为对称轴的对称点,∴OA=OA1,∠3=∠4,同理OA=OA2,∠1=∠2,∴OA1=OA2,且∠1+∠2+∠3+∠4=2(∠1+∠3)=180°,∴点A1,A2是以O为中心的对称点.
17.
(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)点P的坐标为(2,0).
18.
证明:如图,连接AD、BC,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BO=DO,
∵点E、F关于点O对称,
∴OF=OE,
在△BOF和△DOE中,∴△BOF≌△DOE(SAS),
∴BF=DE.
19.
解:(1)AE綊BF.理由:由题意知△ABC与△FEC关于点C成中心对称,
∴点A与点F,点B与点E关于点C成中心对称,
∴线段AE与线段FB关于点C成中心对称,∴AE綊BF
(2)∠ACB=60°时,四边形ABFE为矩形.理由:由(1)知AE綊BF,
∴四边形ABFE是平行四边形,∴AC=FC,BC=EC.∵AB=AC,
∠ACB=60°,∴△ABC是等边三角形,∴AC=BC,∴AF=BE,
∴四边形ABFE为矩形
20.
解析
(1)如图,△A?B?C?即为所求.
(2)由图可知A?(2,1),B?(1,3).
21.
∵△CDA与△ABC关于点O中心对称,AB=6,∠BAC=40°,∴
CD=AB=6,∠ACD=
∠BAC=40°.
一、选择题
1.
剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,如图所示的剪纸图案( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形又不是中心对称图形
2.
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.
2
B.
3
C.
4
D.
1.5
3.如图,平行四边形ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有(
)
A.4对
B.3对
C.2对
D.1对
4.点A和点B的坐标分别为(0,2),(1,0),若将△OAB绕点B顺时针旋转180°后,得到△OAB,则点A的对应点A的坐标是( )
A.(0,2)
B.(2,2)
C.(-2,2) D.(2,-2)
5.
如图所示的四组图形中,左边的图形与右边的图形成中心对称的是( )
A
B
C
D
6.如图,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确的是(
)
A.AB=A′B′,BC=B′C′
B.AB∥A′B′,BC∥B′C′
C.S△ABC=S△A′B′C′
D.△ABC≌△A′OC′
7.
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为( )
A.4 B.12
C.6 D.3
8.
如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2
B.3
C.4
D.1.5
二、填空题
9.
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转180°得到△FEC,若△ABC的面积为3cm2,则四边形ABFE的面积为
.
10.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 .BD∥ 且BD= .连接点A和点F的线段经过点 ,且被C点 ,△ABD≌ .?
11.如图,图形①与图形________成轴对称,图形②与图形________成中心对称.
12.如图,已知AB=3,AC=1,∠D=90°,△DEC
与△ABC关于点C成中心对称,点F是DE的中点,连接CF,则CF的长是 .?
13.如图,已知△ABC与△ADE关于点A成中心对称,若AB=2
cm,那么BD的长为________.
14.
如图,点O是?ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=0.5AB;G,H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是_________.
三、解答题
15.
如图所示,已知△ABC外一点O,画△A′B′C′,使△A′B′C′与△ABC关于O点中心对称.
16.
已知MN⊥PQ,交点为O点,A1,A是以MN为轴的对称点,而A2,A是以PQ为轴的对称点,如图所示.请说明A1,A2是以点O为对称中心的对称点.
17.
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
18.
如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O对称.求证:BF=DE.
19.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
20.△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A?B?C;
(2)写出点A?、B?的坐标.
21.
如图
,在△ABC中,点O是AC
的中点,△CDA与△ABC关于点O中心对称,若AB=6,∠BAC=
40?,则CD的长度是多少,∠ACD的度数是多少.
答案
1.
B
2.
A
3.
A
4.
D
5.
A
6.
D
7.
D
8.
A
9.
12cm2
10.
C;F;D;EG;EG;C;平分;△FGE
11.
④,③
12.
13.
4cm
14.
=
15.
解:如图所示.
16.
证明:如图所示,连接AA1,AA2,OA,OA1,OA2,∵A,A1是以MN为对称轴的对称点,∴OA=OA1,∠3=∠4,同理OA=OA2,∠1=∠2,∴OA1=OA2,且∠1+∠2+∠3+∠4=2(∠1+∠3)=180°,∴点A1,A2是以O为中心的对称点.
17.
(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
(3)点P的坐标为(2,0).
18.
证明:如图,连接AD、BC,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BO=DO,
∵点E、F关于点O对称,
∴OF=OE,
在△BOF和△DOE中,∴△BOF≌△DOE(SAS),
∴BF=DE.
19.
解:(1)AE綊BF.理由:由题意知△ABC与△FEC关于点C成中心对称,
∴点A与点F,点B与点E关于点C成中心对称,
∴线段AE与线段FB关于点C成中心对称,∴AE綊BF
(2)∠ACB=60°时,四边形ABFE为矩形.理由:由(1)知AE綊BF,
∴四边形ABFE是平行四边形,∴AC=FC,BC=EC.∵AB=AC,
∠ACB=60°,∴△ABC是等边三角形,∴AC=BC,∴AF=BE,
∴四边形ABFE为矩形
20.
解析
(1)如图,△A?B?C?即为所求.
(2)由图可知A?(2,1),B?(1,3).
21.
∵△CDA与△ABC关于点O中心对称,AB=6,∠BAC=40°,∴
CD=AB=6,∠ACD=
∠BAC=40°.
同课章节目录
