2020年秋人教版九年级数学上册随堂练23.2.3 关于原点对称的点的坐标随堂练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练23.2.3 关于原点对称的点的坐标随堂练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 13:15:27 | ||
图片预览


文档简介
23.2.3
关于原点对称的点的坐标
随堂练习
一、选择题
1.
直角坐标系中,点P的坐标为(a+5,a-5),则P点关于原点的对称点P不可能在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.
已知点A(m,2)与点A′(6,n)关于坐标原点对称,则实数m,n的值是( )
A.
m=6,n=2
B.
m=-6,n=2
C.
m=6,n=-2
D.
m=-6,n=-2
3.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为(
)
A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
4.在平面直角坐标系中,点P(-3,-5)关于原点对称的点的坐标是(
)
A.(3,-5)
B.(-3,5)
C.(3,5)
D.(-3,-5)
5.
点(-2,5)关于坐标原点对称的点的坐标是( )
A.(2,-5) B.(-2,-5)
C.(2,5) D.(5,-2)
6.
若点P(-1-2a,2a-4)关于原点对称的点是第一象限内的点,则a的整数解有( )
A.
1个
B.
2个
C.
3个
D.
4个
7.
如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(-5,2),(-2,-2),(5,-2),则点D的坐标为(
)
A.(2,2)
B.(2,-2)
C.(2,5)
D.(-2,5)
8.若点P(x,-)与点Q(y,)关于原点对称,则x+y等于( )
A. B.-
C.0
D.2
9.
在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P4,P5,P6,…则点P2
018的坐标是(
)
A.(0,0)
B.(0,2)
C.(2,-4)
D.(-4,2)
二、填空题
10.
已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是
.
11.若点A(-2,n)在x轴上,则点B(n-1,n+1)关于原点对称的点的坐标为 .?
12.
若△ABC的三边为a,b,c,且A(|c-6|,1)与B(,-1)关于原点对称,|a-4|=2,则△ABC的形状是
三角形.
13.
在平面直角坐标系中,点P(2,3)与点P′(2a+b,a+2b)关于原点对称,则a-b的值为____.
14.在平面直角坐标系xOy中,如果有点P(-1,2)与点Q(1,-2),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-2x的图象上.前面的四种描述正确的是 .(填序号)?
15.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,则(x+y)y的值是_______.
三、解答题
16.
已知点(2x,y2+4)与点(x2+1,-4y)关于坐标原点对称,试求x+y的值.
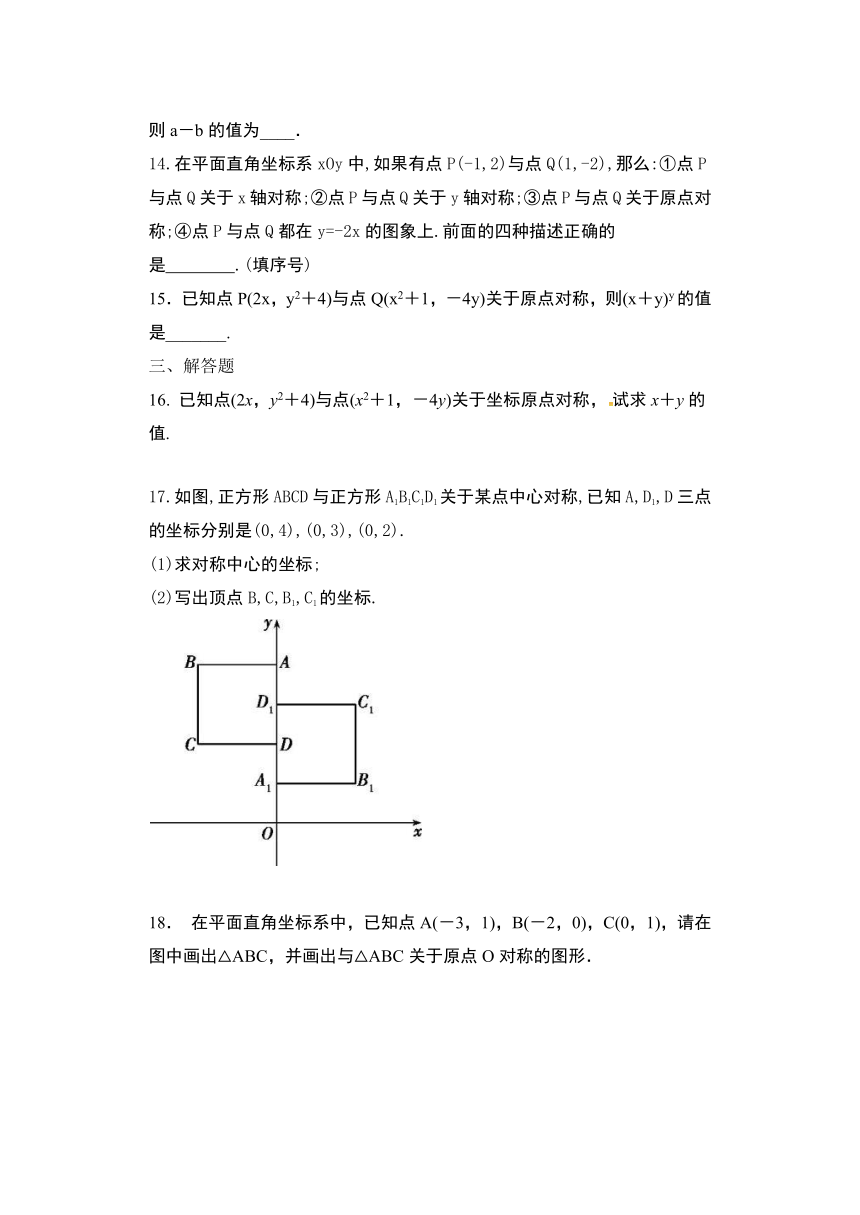
17.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
18.
在平面直角坐标系中,已知点A(-3,1),B(-2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.
19.
在边长为1个单位长度的正方形网格中建立如图的平面直角坐标系xOy,△ABC的顶点都在格点上,请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的△A1B1C1;
(2)若点M是△ABC内一点,其坐标为(a,b),点M在△A1B1C1内的对应点为M1,则点M1的坐标为(a,b-5);
(3)画出△ABC关于点O的中心对称图形△A2B2C2.
20.
如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点O对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
答案
1.
D
2.
D
3.
A
4.
C
5.
A
6.
B
7.
A
8.
C
9.
D
10.
m<0
11.
(1,-1)
12.
等腰
13.
1
14.
③④
15.
1
16.
解:∵点(2x,y2+4)与点(x2+1,-4y)关于坐标原点对称,∴y2+4-4y=0,
(2x+x2+1=0,)解得y=2.
(x=-1,)∴x+y=-1+2=1,即x+y的值是1.
17.
(1)根据中心对称的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上,可得顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
18.
解:如图所示:
19.
解:(1)如图所示△A1B1C1即为所求
(2)∵点M是△ABC内一点,其坐标为(a,b),点M在△A1B1C1内的对应点为M1,
∴点M1的坐标为(a,b-5);故答案为(a,b-5)
(3)如图所示△A2B2C2即为所求
20.
解:(1)图略,A,B,C向左平移5个单位长度后的坐标分别为
(-4,1),(-1,2),(-2,4),连接这三个点,得△A1B1C1
(2)图略,A,B,C关于原点的对称点的坐标分别为
(-1,-1),(-4,-2),(-3,-4),连接这三个点,得△A2B2C2
(3)图略,P(2,0).作点A关于x轴的对称点A′,
连接A′B交x轴于点P,则点P即为所求作的点
关于原点对称的点的坐标
随堂练习
一、选择题
1.
直角坐标系中,点P的坐标为(a+5,a-5),则P点关于原点的对称点P不可能在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.
已知点A(m,2)与点A′(6,n)关于坐标原点对称,则实数m,n的值是( )
A.
m=6,n=2
B.
m=-6,n=2
C.
m=6,n=-2
D.
m=-6,n=-2
3.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为(
)
A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
4.在平面直角坐标系中,点P(-3,-5)关于原点对称的点的坐标是(
)
A.(3,-5)
B.(-3,5)
C.(3,5)
D.(-3,-5)
5.
点(-2,5)关于坐标原点对称的点的坐标是( )
A.(2,-5) B.(-2,-5)
C.(2,5) D.(5,-2)
6.
若点P(-1-2a,2a-4)关于原点对称的点是第一象限内的点,则a的整数解有( )
A.
1个
B.
2个
C.
3个
D.
4个
7.
如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(-5,2),(-2,-2),(5,-2),则点D的坐标为(
)
A.(2,2)
B.(2,-2)
C.(2,5)
D.(-2,5)
8.若点P(x,-)与点Q(y,)关于原点对称,则x+y等于( )
A. B.-
C.0
D.2
9.
在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称中心重复前面的操作,依次得到P4,P5,P6,…则点P2
018的坐标是(
)
A.(0,0)
B.(0,2)
C.(2,-4)
D.(-4,2)
二、填空题
10.
已知点M(-,3m)关于原点对称的点在第一象限,那么m的取值范围是
.
11.若点A(-2,n)在x轴上,则点B(n-1,n+1)关于原点对称的点的坐标为 .?
12.
若△ABC的三边为a,b,c,且A(|c-6|,1)与B(,-1)关于原点对称,|a-4|=2,则△ABC的形状是
三角形.
13.
在平面直角坐标系中,点P(2,3)与点P′(2a+b,a+2b)关于原点对称,则a-b的值为____.
14.在平面直角坐标系xOy中,如果有点P(-1,2)与点Q(1,-2),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-2x的图象上.前面的四种描述正确的是 .(填序号)?
15.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,则(x+y)y的值是_______.
三、解答题
16.
已知点(2x,y2+4)与点(x2+1,-4y)关于坐标原点对称,试求x+y的值.
17.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
18.
在平面直角坐标系中,已知点A(-3,1),B(-2,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的图形.
19.
在边长为1个单位长度的正方形网格中建立如图的平面直角坐标系xOy,△ABC的顶点都在格点上,请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的△A1B1C1;
(2)若点M是△ABC内一点,其坐标为(a,b),点M在△A1B1C1内的对应点为M1,则点M1的坐标为(a,b-5);
(3)画出△ABC关于点O的中心对称图形△A2B2C2.
20.
如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点O对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
答案
1.
D
2.
D
3.
A
4.
C
5.
A
6.
B
7.
A
8.
C
9.
D
10.
m<0
11.
(1,-1)
12.
等腰
13.
1
14.
③④
15.
1
16.
解:∵点(2x,y2+4)与点(x2+1,-4y)关于坐标原点对称,∴y2+4-4y=0,
(2x+x2+1=0,)解得y=2.
(x=-1,)∴x+y=-1+2=1,即x+y的值是1.
17.
(1)根据中心对称的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上,可得顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
18.
解:如图所示:
19.
解:(1)如图所示△A1B1C1即为所求
(2)∵点M是△ABC内一点,其坐标为(a,b),点M在△A1B1C1内的对应点为M1,
∴点M1的坐标为(a,b-5);故答案为(a,b-5)
(3)如图所示△A2B2C2即为所求
20.
解:(1)图略,A,B,C向左平移5个单位长度后的坐标分别为
(-4,1),(-1,2),(-2,4),连接这三个点,得△A1B1C1
(2)图略,A,B,C关于原点的对称点的坐标分别为
(-1,-1),(-4,-2),(-3,-4),连接这三个点,得△A2B2C2
(3)图略,P(2,0).作点A关于x轴的对称点A′,
连接A′B交x轴于点P,则点P即为所求作的点
同课章节目录
