2020年秋人教版九年级数学上册随堂练23.2.3 关于原点对称的点的坐标提升练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练23.2.3 关于原点对称的点的坐标提升练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 443.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 13:16:30 | ||
图片预览


文档简介
23.2.3
关于原点对称的点的坐标
提升练习
一、选择题
1.
在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为(
)
A.(3,2)
B.(2,-3)
C.(-3,-2)
D.(3,-2)
2.在A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)和G(-2,-1)这七个点中,关于原点O对称的两个点是( )
A.A和E B.B和D
C.C和F D.F和G
3.如图,在平面直角坐标系中,?MNEF的两条对角线ME,NF交于原点O,点F的坐标是(3,2),则点N的坐标为(
)
A.(-3,-2)
B.(-3,2)
C.(-2,3)
D.(2,3)
4.
已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a,b的值是( )
A.
a=5,b=1
B.
a=-5,b=1
C.
a=5,b=-1
D.
a=-5,b=-1
5.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是(
)
A.(-3,2)
B.(-1,2)
C.(1,2)
D.(1,-2)
6.若点P(m,2)与点Q(5,n)关于原点对称,则顶点为(m,n),形状与y=2x2相同的抛物线是( )
A.y=2(x-5)2-2 B.y=2(x+5)2-2
C.y=2(x-5)2+2 D.y=2(x+5)2+2
7.
已知菱形ABCD在平面直角坐标系中的位置如图所示,若AD边的中点P的坐标为(1.5,2),则BC边的中点Q的坐标是( )
A.
(-1.5,-2)
B.
(-2,-1.5)
C.
(-3,-2)
D.
(-3,-4)
8.
将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是( )
A.
(-3,2)
B.
(-1,2)
C.
(1,2)
D.
(1,-2)
9.
以下每对函数,其图象一定关于原点对称的是( )
A.y=x2与y=-2x2
B.y=x2+1与y=-x2
C.y=x2+1与y=-x2-1
D.y=(x-1)2与y=(x+1)2
二、填空题
10.
已知△ABC在平面直角坐标系上三顶点坐标为A(-2,3),B(-1,1),C(-3,2),△A1B1C1与△ABC关于原点对称,则A1
,B1
,C1
.
11.抛物线y=x2-2x-3关于原点对称的抛物线的解析式为________.
12.在平面直角坐标系中,点P(1,5)与点P(2a+b,a+2b)关于原点对称,则a2-b2的值为 .?
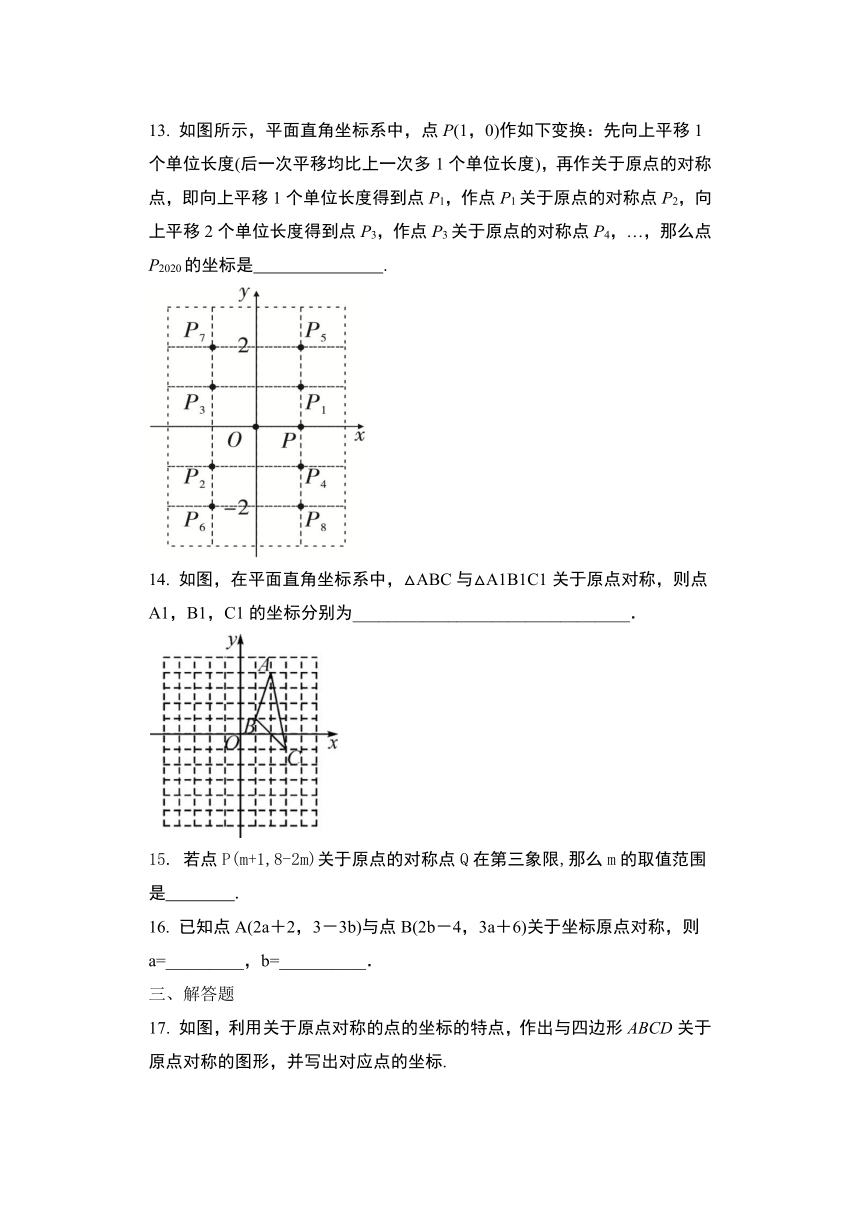
13.
如图所示,平面直角坐标系中,点P(1,0)作如下变换:先向上平移1个单位长度(后一次平移均比上一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4,…,那么点P2020的坐标是
.
14.
如图,在平面直角坐标系中,△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为________________________________.
15.
若点P(m+1,8-2m)关于原点的对称点Q在第三象限,那么m的取值范围是 .?
16.
已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,则a=_________,b=__________.
三、解答题
17.
如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形,并写出对应点的坐标.
18.
△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标;
(4)求△ABC的面积.
19.
如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(-1,5),B(-4,2),C(-2,2).
(1)平移△ABC,使点B移动到点B1(1,1),画出平移后的△A1B1C1,并写出点A1,C1的坐标;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)求线段AA1的长度.
20.
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
答案
1.
D
2.
C
3.
A
4.
D
5.
D
6.
B
7.
A
8.
D
9.
C
10.
(2,-3)
(1,-1)
(3,-2)
11.
y=-x2-2x+3
12.
-8
13.
(1,-505)
14.
(-2,-4),(-1,-1),(-3,1)
15.
-116.
-1,
2
17.
解:如图所示,两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此四边形ABCD的四个顶点A(-2,3),B(-4,1),C(-3,-1),D(-1,0)关于原点的对称点分别为A′(2,-3),B′(4,-1),C′(3,1),D′(1,0),依次连接A′B′,B′C′,C′D′,D′A′,就可得到与四边形ABCD关于原点对称的四边形A′B′C′D′.
18.
(1)A(0,3),B(-4,4),C(-2,1).
(2)如图所示,△A1B1C1即为所求,B1的坐标为(4,4).
(3)如图所示,△A2B2C2即为所求,A2的坐标为(0,-3).
(4)△ABC的面积为4×3-×2×2-×2×3-×1×4=5.
19.
解:(1)平移后的△A1B1C1如图所示,点A1(4,4),C1(3,1)
(2)△ABC关于原点O对称的△A2B2C2如图所示
(3)AA1==.故答案为
20.
解:(1)如图,△A1B1C1为所作,C1(-1,2)
(2)如图,△A2B2C2为所作,C2(-3,-2)
(3)∵A的坐标为(2,4),A3的坐标为(-4,-2),
∴直线l的函数解析式为y=-x
关于原点对称的点的坐标
提升练习
一、选择题
1.
在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为(
)
A.(3,2)
B.(2,-3)
C.(-3,-2)
D.(3,-2)
2.在A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)和G(-2,-1)这七个点中,关于原点O对称的两个点是( )
A.A和E B.B和D
C.C和F D.F和G
3.如图,在平面直角坐标系中,?MNEF的两条对角线ME,NF交于原点O,点F的坐标是(3,2),则点N的坐标为(
)
A.(-3,-2)
B.(-3,2)
C.(-2,3)
D.(2,3)
4.
已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a,b的值是( )
A.
a=5,b=1
B.
a=-5,b=1
C.
a=5,b=-1
D.
a=-5,b=-1
5.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是(
)
A.(-3,2)
B.(-1,2)
C.(1,2)
D.(1,-2)
6.若点P(m,2)与点Q(5,n)关于原点对称,则顶点为(m,n),形状与y=2x2相同的抛物线是( )
A.y=2(x-5)2-2 B.y=2(x+5)2-2
C.y=2(x-5)2+2 D.y=2(x+5)2+2
7.
已知菱形ABCD在平面直角坐标系中的位置如图所示,若AD边的中点P的坐标为(1.5,2),则BC边的中点Q的坐标是( )
A.
(-1.5,-2)
B.
(-2,-1.5)
C.
(-3,-2)
D.
(-3,-4)
8.
将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是( )
A.
(-3,2)
B.
(-1,2)
C.
(1,2)
D.
(1,-2)
9.
以下每对函数,其图象一定关于原点对称的是( )
A.y=x2与y=-2x2
B.y=x2+1与y=-x2
C.y=x2+1与y=-x2-1
D.y=(x-1)2与y=(x+1)2
二、填空题
10.
已知△ABC在平面直角坐标系上三顶点坐标为A(-2,3),B(-1,1),C(-3,2),△A1B1C1与△ABC关于原点对称,则A1
,B1
,C1
.
11.抛物线y=x2-2x-3关于原点对称的抛物线的解析式为________.
12.在平面直角坐标系中,点P(1,5)与点P(2a+b,a+2b)关于原点对称,则a2-b2的值为 .?
13.
如图所示,平面直角坐标系中,点P(1,0)作如下变换:先向上平移1个单位长度(后一次平移均比上一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4,…,那么点P2020的坐标是
.
14.
如图,在平面直角坐标系中,△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为________________________________.
15.
若点P(m+1,8-2m)关于原点的对称点Q在第三象限,那么m的取值范围是 .?
16.
已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,则a=_________,b=__________.
三、解答题
17.
如图,利用关于原点对称的点的坐标的特点,作出与四边形ABCD关于原点对称的图形,并写出对应点的坐标.
18.
△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标;
(4)求△ABC的面积.
19.
如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(-1,5),B(-4,2),C(-2,2).
(1)平移△ABC,使点B移动到点B1(1,1),画出平移后的△A1B1C1,并写出点A1,C1的坐标;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)求线段AA1的长度.
20.
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
答案
1.
D
2.
C
3.
A
4.
D
5.
D
6.
B
7.
A
8.
D
9.
C
10.
(2,-3)
(1,-1)
(3,-2)
11.
y=-x2-2x+3
12.
-8
13.
(1,-505)
14.
(-2,-4),(-1,-1),(-3,1)
15.
-1
-1,
2
17.
解:如图所示,两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y).因此四边形ABCD的四个顶点A(-2,3),B(-4,1),C(-3,-1),D(-1,0)关于原点的对称点分别为A′(2,-3),B′(4,-1),C′(3,1),D′(1,0),依次连接A′B′,B′C′,C′D′,D′A′,就可得到与四边形ABCD关于原点对称的四边形A′B′C′D′.
18.
(1)A(0,3),B(-4,4),C(-2,1).
(2)如图所示,△A1B1C1即为所求,B1的坐标为(4,4).
(3)如图所示,△A2B2C2即为所求,A2的坐标为(0,-3).
(4)△ABC的面积为4×3-×2×2-×2×3-×1×4=5.
19.
解:(1)平移后的△A1B1C1如图所示,点A1(4,4),C1(3,1)
(2)△ABC关于原点O对称的△A2B2C2如图所示
(3)AA1==.故答案为
20.
解:(1)如图,△A1B1C1为所作,C1(-1,2)
(2)如图,△A2B2C2为所作,C2(-3,-2)
(3)∵A的坐标为(2,4),A3的坐标为(-4,-2),
∴直线l的函数解析式为y=-x
同课章节目录
