新人教版数学八年级上册14.3.2 因式分解之十字相乘法和分组分解法课件(19张ppt)
文档属性
| 名称 | 新人教版数学八年级上册14.3.2 因式分解之十字相乘法和分组分解法课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览


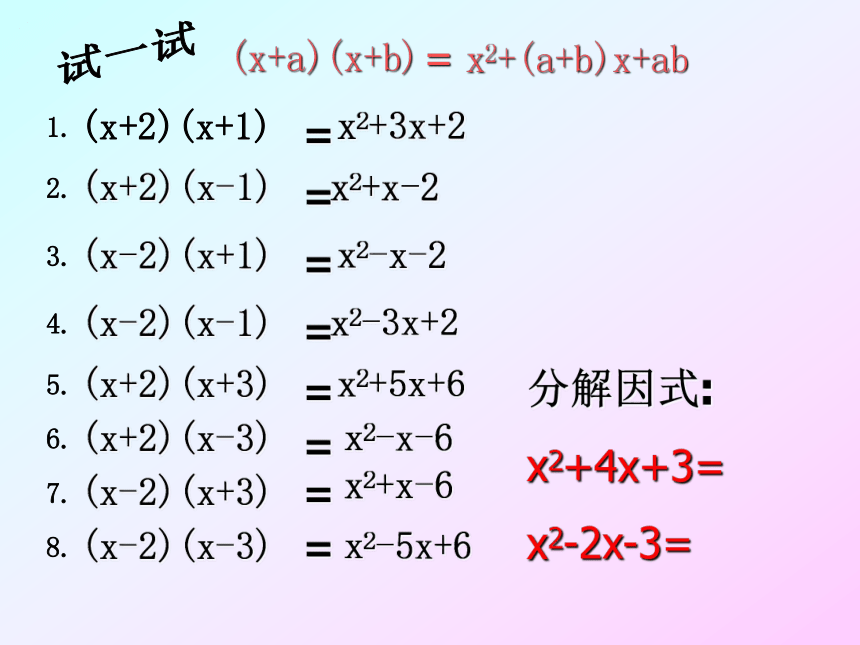



文档简介
(共19张PPT)
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
分解因式:
x2+4x+3=
x2-2x-3=
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.
用十字相乘法把形如x2+px+q的二次三项式分解因式:
当q>0时,q分解的因数a、b( )
当q<0时,q分解的因数a、b( )
同号
异号
知识要点
q=ab,p=a+b
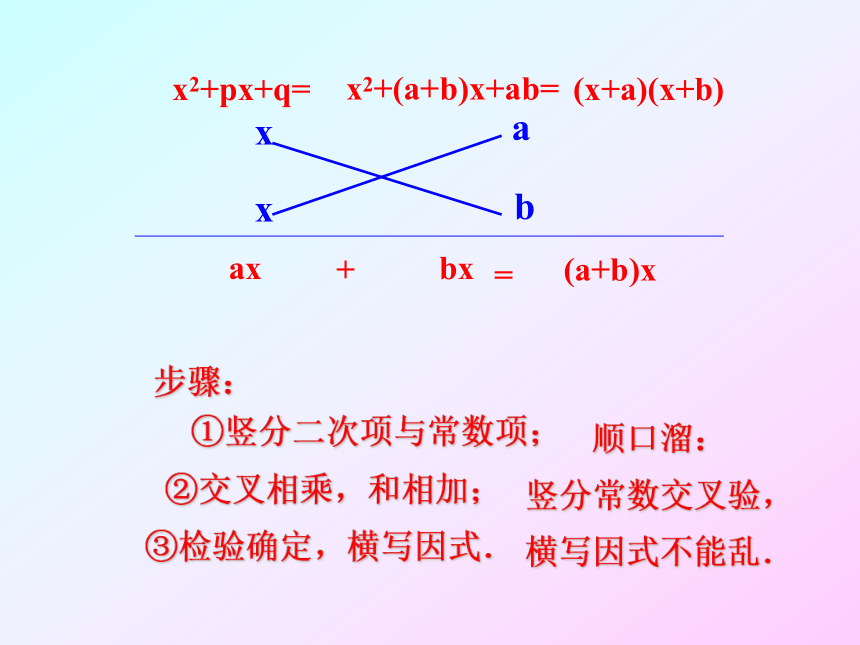
x2+px+q=
x2+(a+b)x+ab=
x
x
a
b
ax
+
bx
=
(a+b)x
(x+a)(x+b)
步骤:
①竖分二次项与常数项;
②交叉相乘,和相加;
③检验确定,横写因式.
顺口溜:
竖分常数交叉验,
横写因式不能乱.
1.x2+8x+12=
2.x2-11x-12=
3.x2-7x+12=
4.x2-4x-12=
(x+2)(x+6)
(x-6)(x+2)
(x-3)(x-4)
(x-12)(x+1)
5.x2+13x+12=
(x+1)(x+12)
6.x2-x-12=
(x-4)(x+3)
将下列各式因式分解:
对二次三项式x2+px+q进行因式分解,应重点掌握以下三个问题:
1.掌握方法:拆分常数项,验证一次项.
2.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
3.书写格式:竖分横积.
注意
知识要点
分组分解法分解因式:
如果一个多项式适当分组,使分组后各组之间有公因式或可应用公式,那么这个多项式就可以用分组的方法分解因式。
mx+my-nx-ny
①
②
③
④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny)
=m(x+y)-n(x+y)
=(x+y)(m-n)
①③,②④两组,得(mx-nx)+(my-ny)
解2:原式= (mx-nx)+(my-ny)
=x(m-n)+y(m-n)
= (m-n) (x+y)
练一练
(1)分组时小组内能提公因式要保证组与组
之间还有公因式可以提.
(2)分组添括号时要注意符号的变化.
(3)要将分解到底,不同分组的结果应该是
一样的.
注意
把下列各式因式分解:
练一练
(1)x2+2xy+y2-z2 (2)ab+a+b+1
解:(1)原式=(x2+2xy+y2)-z2
=(x+y)2-z2
=(x+y+z)(x+y-z)
(2)原式=(ab+a)+(b+1)
=a(b+1)+(b+1)
=(b+1)(a+1)
(3)9a4-4a2+4a-1
解:9a4-4a2+4a-1
= 9a4-(4a2-4a+1)
= 9a4-(2a-1) 2
= (3a2+2a-1)(3a2-2a+1)
= (a+1)(3a-1)(3a2-2a+1)
(4)(x-1)(x+2)(x-3)(x+4)+24
解:(x-1)(x+2)(x-3)(x+4)+24
= (x2+x-2)(x2+x-12)+24
= (x2+x) 2-14(x2+x)+48
= (x2+x-6)(x2+x-8)
= (x+3)(x-2)(x2+x-8)
(2007年株洲市)
分解因式(x4+x2-4)(x4+x2+3)+10
解:令x4+x2=m,则原式可化为
(m-4)(m+3)+10
= m2-m-12+10
= m2-m-2
= (m-2)(m+1)
= (x4+x2-2)(x4+x2+1)
= (x2+2)(x2-1)(x4+x2+1)
= (x2+2)(x+1)(x-1)(x4+x2+1)
如果a+b=0,求a3 –2b3+ a2b –2ab2的值.
原式= a3 +a2b- (2b3 +2ab2 )
= a2 (a +b)- 2b2 (a +b )
= (a +b) ( a2 - 2b2 )
练一练
=0
解:4x4+1
= 4x4+4x2+1-4x2
=(2x2+1)2-(2x)2
=( 2x2+1+ 2x)( 2x2+1-2x)
因式分解:4x4+1
因式分解是多项式乘法的逆运算.在多项式乘法运算时,整理、化简常将几个同类项合并为一项,或将两个仅符号相反的同类项相互抵消为零.在对某些多项式分解因式时,需要恢复那些被合并或相互抵消的项,即把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符合相反的项,前者称为拆项,后者称为添项.拆项、添项的目的是使多项式能用分组分解法进行因式分解.
注意
用十字相乘法进行因式分解:
(x+2)(x-3)
1.x2-x- 6 =
(x-3)(x+5)
2.x2+2x-15=
(x+2)(x-5)
3.x2-3x-10=
(x-5)(x-4)
4.x2-9x+20=
(x-7)(x+4)
5.x2-3x-28=
(x+2)(x-4)
6.x2-2x-8=
(x-1)(x-3)
7.x2-4x+3=
(x+3)(x+4)
(x+2)(x+3)
(x-3)(x+7)
8.x2+7x+12=
9.x2+5x+6=
10.x2+4x-21=
(y+12)(y-3)
11.y2+9y-36=
(y-9)(y+14)
(y+4)(y-15)
(y-7)(y+16)
(y-8)(y-17)
(y+16)(y+3)
(y+19)(y-7)
(y+11)(y-10)
(y-13)(y-3)
(y+14)(y+4)
13.y2-11y-60=
12.y2+5y-126=
14.y2+9y-112=
15.y2-25y+136=
16.y2+19y+48=
17.y2+12y-133=
18.y2+y-110=
19.y2-16y+39=
20.y2+18y+56=
先填空,再分解(尽可能多的)
x2 ( )x+60=( )( )
1.(x+2)(x+1)=
x2+3x+2
3.(x-2)(x+1)=
x2-x-2
4.(x-2)(x-1)=
x2-3x+2
2.(x+2)(x-1)=
x2+x-2
5.(x+2)(x+3)=
x2+5x+6
6.(x+2)(x-3)=
x2-x-6
7.(x-2)(x+3)=
x2+x-6
8.(x-2)(x-3)=
x2-5x+6
(x+a)(x+b)
=x2+(a+b)x+ab
请直接口答计算结果:
(x+2)(x+1)
x2+3x+2
(x-2)(x+1)
x2-x-2
(x-2)(x-1)
x2-3x+2
(x+2)(x-1)
x2+x-2
(x+2)(x+3)
x2+5x+6
(x+2)(x-3)
x2-x-6
(x-2)(x+3)
x2+x-6
(x-2)(x-3)
x2-5x+6
(x+a)(x+b)
=
x2+(a+b)x+ab
=
=
=
=
=
=
=
=
1.
2.
3.
4.
5.
6.
7.
8.
分解因式:
x2+4x+3=
x2-2x-3=
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.
用十字相乘法把形如x2+px+q的二次三项式分解因式:
当q>0时,q分解的因数a、b( )
当q<0时,q分解的因数a、b( )
同号
异号
知识要点
q=ab,p=a+b
x2+px+q=
x2+(a+b)x+ab=
x
x
a
b
ax
+
bx
=
(a+b)x
(x+a)(x+b)
步骤:
①竖分二次项与常数项;
②交叉相乘,和相加;
③检验确定,横写因式.
顺口溜:
竖分常数交叉验,
横写因式不能乱.
1.x2+8x+12=
2.x2-11x-12=
3.x2-7x+12=
4.x2-4x-12=
(x+2)(x+6)
(x-6)(x+2)
(x-3)(x-4)
(x-12)(x+1)
5.x2+13x+12=
(x+1)(x+12)
6.x2-x-12=
(x-4)(x+3)
将下列各式因式分解:
对二次三项式x2+px+q进行因式分解,应重点掌握以下三个问题:
1.掌握方法:拆分常数项,验证一次项.
2.符号规律:
当q>0时,a、b同号,且a、b的符号与p的符号相同;
当q<0时,a、b异号,且绝对值较大的因数与p的符号相同.
3.书写格式:竖分横积.
注意
知识要点
分组分解法分解因式:
如果一个多项式适当分组,使分组后各组之间有公因式或可应用公式,那么这个多项式就可以用分组的方法分解因式。
mx+my-nx-ny
①
②
③
④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny)
=m(x+y)-n(x+y)
=(x+y)(m-n)
①③,②④两组,得(mx-nx)+(my-ny)
解2:原式= (mx-nx)+(my-ny)
=x(m-n)+y(m-n)
= (m-n) (x+y)
练一练
(1)分组时小组内能提公因式要保证组与组
之间还有公因式可以提.
(2)分组添括号时要注意符号的变化.
(3)要将分解到底,不同分组的结果应该是
一样的.
注意
把下列各式因式分解:
练一练
(1)x2+2xy+y2-z2 (2)ab+a+b+1
解:(1)原式=(x2+2xy+y2)-z2
=(x+y)2-z2
=(x+y+z)(x+y-z)
(2)原式=(ab+a)+(b+1)
=a(b+1)+(b+1)
=(b+1)(a+1)
(3)9a4-4a2+4a-1
解:9a4-4a2+4a-1
= 9a4-(4a2-4a+1)
= 9a4-(2a-1) 2
= (3a2+2a-1)(3a2-2a+1)
= (a+1)(3a-1)(3a2-2a+1)
(4)(x-1)(x+2)(x-3)(x+4)+24
解:(x-1)(x+2)(x-3)(x+4)+24
= (x2+x-2)(x2+x-12)+24
= (x2+x) 2-14(x2+x)+48
= (x2+x-6)(x2+x-8)
= (x+3)(x-2)(x2+x-8)
(2007年株洲市)
分解因式(x4+x2-4)(x4+x2+3)+10
解:令x4+x2=m,则原式可化为
(m-4)(m+3)+10
= m2-m-12+10
= m2-m-2
= (m-2)(m+1)
= (x4+x2-2)(x4+x2+1)
= (x2+2)(x2-1)(x4+x2+1)
= (x2+2)(x+1)(x-1)(x4+x2+1)
如果a+b=0,求a3 –2b3+ a2b –2ab2的值.
原式= a3 +a2b- (2b3 +2ab2 )
= a2 (a +b)- 2b2 (a +b )
= (a +b) ( a2 - 2b2 )
练一练
=0
解:4x4+1
= 4x4+4x2+1-4x2
=(2x2+1)2-(2x)2
=( 2x2+1+ 2x)( 2x2+1-2x)
因式分解:4x4+1
因式分解是多项式乘法的逆运算.在多项式乘法运算时,整理、化简常将几个同类项合并为一项,或将两个仅符号相反的同类项相互抵消为零.在对某些多项式分解因式时,需要恢复那些被合并或相互抵消的项,即把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符合相反的项,前者称为拆项,后者称为添项.拆项、添项的目的是使多项式能用分组分解法进行因式分解.
注意
用十字相乘法进行因式分解:
(x+2)(x-3)
1.x2-x- 6 =
(x-3)(x+5)
2.x2+2x-15=
(x+2)(x-5)
3.x2-3x-10=
(x-5)(x-4)
4.x2-9x+20=
(x-7)(x+4)
5.x2-3x-28=
(x+2)(x-4)
6.x2-2x-8=
(x-1)(x-3)
7.x2-4x+3=
(x+3)(x+4)
(x+2)(x+3)
(x-3)(x+7)
8.x2+7x+12=
9.x2+5x+6=
10.x2+4x-21=
(y+12)(y-3)
11.y2+9y-36=
(y-9)(y+14)
(y+4)(y-15)
(y-7)(y+16)
(y-8)(y-17)
(y+16)(y+3)
(y+19)(y-7)
(y+11)(y-10)
(y-13)(y-3)
(y+14)(y+4)
13.y2-11y-60=
12.y2+5y-126=
14.y2+9y-112=
15.y2-25y+136=
16.y2+19y+48=
17.y2+12y-133=
18.y2+y-110=
19.y2-16y+39=
20.y2+18y+56=
先填空,再分解(尽可能多的)
x2 ( )x+60=( )( )
