1.2 运动的合成与分解课件 25张PPT
文档属性
| 名称 | 1.2 运动的合成与分解课件 25张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 756.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-04 00:00:00 | ||
图片预览





文档简介
第一章 抛体运动
1.2 运动的合成与分解
学习目标定位
知道什么是运动的合成与分解,理解合运动与分运动等有
关物理量之间的关系.
会确定互成角度的两个分运动的合运动性质.
会分析小船渡河问题.
知识储备区
一、1.实际运动
2.相互替代 合成 平行四边形
3.相互替代 平行四边形
二、合成 分解
学习探究区
一、位移和速度的合成与分解
二、小船渡河问题
三、关联物体速度的分解
一、位移和速度的合成与分解
学习·探究区
问题设计
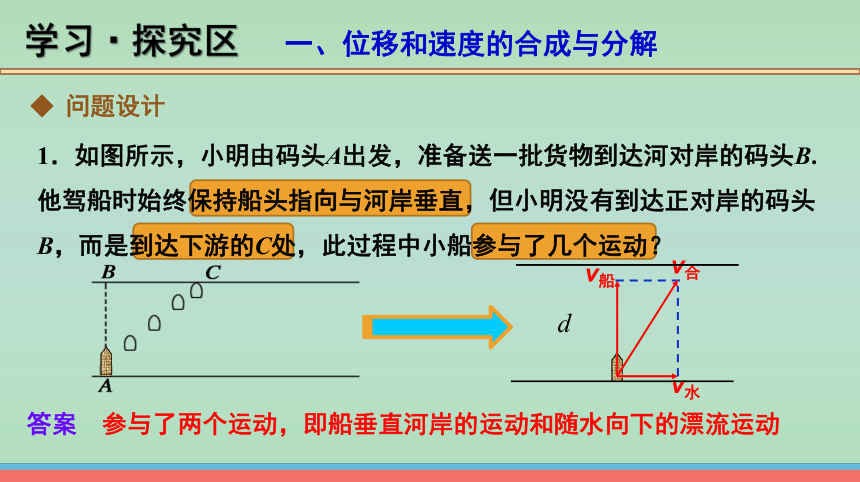
1.如图所示,小明由码头A出发,准备送一批货物到达河对岸的码头B.他驾船时始终保持船头指向与河岸垂直,但小明没有到达正对岸的码头B,而是到达下游的C处,此过程中小船参与了几个运动?
v水
v船
v合
答案 参与了两个运动,即船垂直河岸的运动和随水向下的漂流运动
一、位移和速度的合成与分解
学习·探究区
问题设计
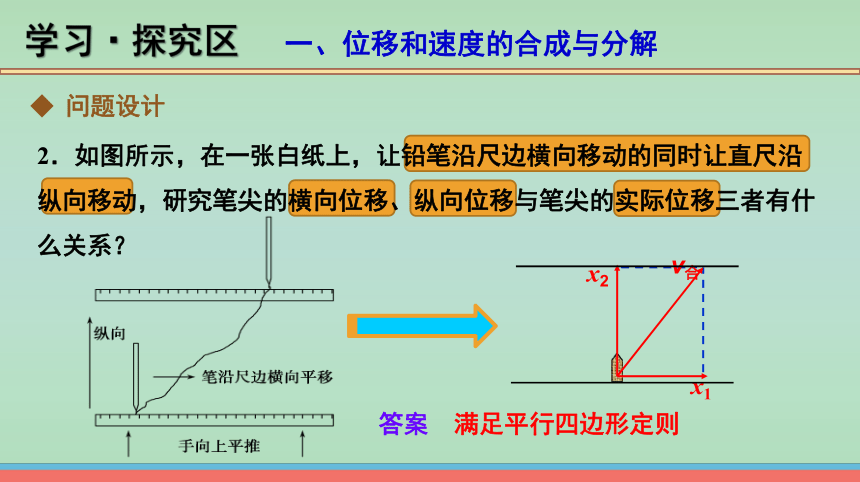
2.如图所示,在一张白纸上,让铅笔沿尺边横向移动的同时让直尺沿纵向移动,研究笔尖的横向位移、纵向位移与笔尖的实际位移三者有什么关系?
x1
x2
v合
答案 满足平行四边形定则
一、位移和速度的合成与分解
2. 合运动与分运动的关系:
(1)等时性:合运动与分运动经历的 相等,即同时开始,同时进行,同时停止.
学习·探究区
(2)独立性:一个物体同时参与了几个分运动,各分运动 、互不影响,因此在研究某个分运动时,就可以不考虑其他分运动,就像其他分运动不存在一样.
(3)等效性:各分运动的相应参量叠加起来与 的参量相同.
1.位移和速度的合成与分解都遵循 定则.
平行四边形
时间
独立进行
合运动
分析两个直线运动的合运动的性质时,应先根据平行四边形定则,求出合运动的合初速度v0和合加速度a,然后进行判断.
(1)判断是否做匀变速运动
学习·探究区
①若a=0时,物体沿合初速度v0的方向做匀速直线运动.
②若a≠0且a恒定时,做匀变速运动.
③若a≠0且a变化时,做非匀变速运动.
(2)判断轨迹的曲直
①若a与速度共线,则做直线运动.
②若a与速度不共线,则做曲线运动.
3. 合运动性质的判断
一、位移和速度的合成与分解
返回
二、小船渡河问题
小船渡河问题一般有渡河时间最短和航程最短两类问题:
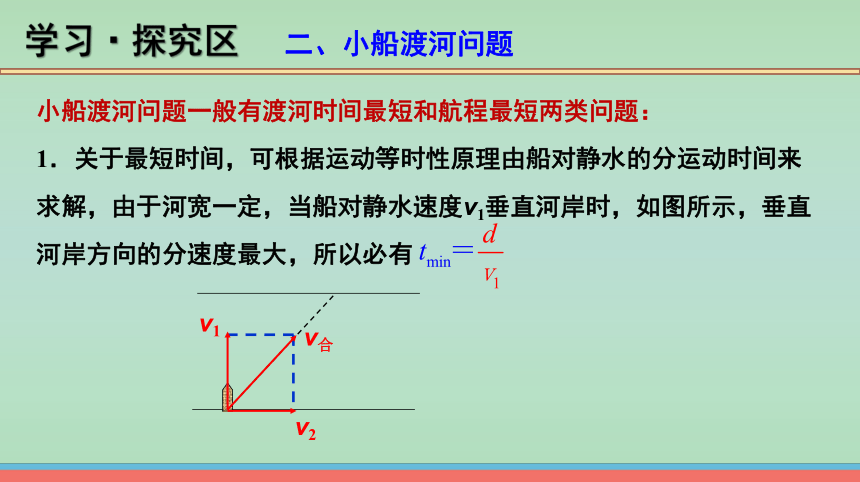
1.关于最短时间,可根据运动等时性原理由船对静水的分运动时间来求解,由于河宽一定,当船对静水速度v1垂直河岸时,如图所示,垂直河岸方向的分速度最大,所以必有
学习·探究区
v2
v1
v合
二、小船渡河问题
学习·探究区
小船渡河问题一般有渡河时间最短和航程最短两类问题:
2.关于最短航程,一般考察水流速度v2小于船对静水速度v1的情况较多,此种情况船的最短航程就等于河宽d,此时船头指向应与上游河岸成θ角(如图所示),且cos θ= ;若v2>v1,则最短航程s= d,此时船头指向应与上游河岸成θ′角,且cos θ′= .
v2
v1
v合
返回
三、关联物体的速度分解问题
绳、杆等连接的两个物体在运动过程中,其速度通常是不一样的,但两者的速度是有联系的(一般两个物体沿绳或杆方向的速度大小相等),我们称之为“关联”速度.解决此类问题的一般步骤如下:
学习·探究区
第一步:先确定合运动,物体的实际运动就是合运动;
第二步:确定合运动的两个实际作用效果:
一是沿牵引方向的平动效果,改变速度的大小;
二是沿垂直于牵引方向的转动效果,改变速度的方向;
第三步:按平行四边形定则进行分解,作好运动矢量图;
第四步:根据沿绳(或杆)牵引方向的速度相等列方程.
三、关联物体的速度分解问题
例如,小车通过跨过滑轮的绳牵引小船B,某一时刻绳与水平方向的夹角为θ,如图所示.
学习·探究区
小船速度vB有两个效果(两个分运动)
一是沿绳方向的平动,
二是垂直绳方向的转动.
将vB沿着这两个方向分解,
v1=vBcos θ=vA
v2=vBsin θ
返回
一、运动的合成与分解
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:ax=0
(1)物体所受的合力:
匀加:
沿y轴正方向
解析
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:vx0=3ms
?
(2)物体的初速度为:
匀加:
沿x轴正方向
解析
一、运动的合成与分解
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:vx=3ms
?
(3)合速度:
匀加:
解析
一、运动的合成与分解
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:x=12 m
(4)合位移:
匀加:
解析
返回
典例精析
一、运动的合成与分解
二、小船渡河问题
例2 已知某船在静水中的速率为v1=4 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,河水的流动速度为v2=3 m/s,方向与河岸平行.试分析:
(1)欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移是多大?
(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
解析:
(1)船头垂直对岸,渡河时间最短
船的位移为
到达对岸A处,顺水漂流的位移
x=v2tmin=3×25 m=75 m
返回
典例精析
二、小船渡河问题
例2 已知某船在静水中的速率为v1=4 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,河水的流动速度为v2=3 m/s,方向与河岸平行.试分析:
(1)欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移是多大?
(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
(2)v1>v2,合速度与河岸垂直,航行距离最短.
设船头与河岸成θ角
船的合速度为
返回
典例精析
例3 如图所示,做匀速直线运动的汽车A通过一根绕过定滑轮的长绳吊起一重物B,设重物和汽车的速度的大小分别为vB、vA,则( )
A.vA=vB B.vA<vB
C.vA>vB D.重物B的速度逐渐增大
三、关联物体速度的分解
两个运动效果
一是使绳子伸长
二是使绳子转动
归属于绳子头问题:
实际速度为合速度
关联
vB=vA cosα
CD
返回
典例精析
自我检测区
1
2
3
4
1.(合运动与分运动的关系)对于两个分运动的合运动,下列说法正确的是( )
A.合运动的速度大小等于两个分运
动的速度大小之和
B.合运动的速度一定大于某一个分
运动的速度
C.合运动的方向就是物体实际运动
的方向
D.由两个分速度的大小就可以确定
合速度的大小
C
1
2
3
4
可能大于分运动,
也可能小于分运动
还需要知道分运动的方向
解析
2.(合运动运动性质的判断)关于运动的合成,下列说法中正确的是( )
A.两个直线运动的合运动,一定是直线
运动
B.两个直线运动的合运动,可能是曲线
运动
C.两个互成角度的匀速直线运动的合运
动,一定是匀速直线运动
D.两个互成角度的匀加速直线运动的合
运动,一定是匀加速直线运动
a合与v合
方向
取决于
共线
直线运动
不共线
曲线运动
a1=0
a2=0
a合=0
v 1恒定
v 2恒定
v 合恒定
匀速
直线
v 2
v 1
v 合
a 1
a 合
a2
匀加速直线
v 2
v 1
v 合
a 1
a 合
a2
匀加速曲线
BC
解析
1
2
3
4
3.(关联物体速度的分解)如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动.则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
A.F不变、v不变
B.F增大、v不变
C.F增大、v增大
D.F增大、v减小
Fcos θ=mg
受力分析
θ
受力平衡
θ
cos θ
F
解析
1
2
3
4
3.(关联物体速度的分解)如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动.则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
A.F不变、v不变
B.F增大、v不变
C.F增大、v增大
D.F增大、v减小
v=v物cos θ
运动分析
θ
θ
cos θ
v
分解速度
解析
1
2
3
4
4.小船在200 m宽的河中横渡,水流速度是2 m/s,小船在静水中的航速是4 m/s.求:
(1)要使小船渡河耗时最少,应如何航行?最短时间为多少?
(2)要使小船航程最短,应如何航行
?最短航程为多少?
垂直河岸
分速度最大
(1)船头朝正对岸耗时最少
v水
v船
v合
(2)v合垂直对岸,航程最短为d
解得
解析
v水
v船
v合
1
2
3
4
1.2 运动的合成与分解
学习目标定位
知道什么是运动的合成与分解,理解合运动与分运动等有
关物理量之间的关系.
会确定互成角度的两个分运动的合运动性质.
会分析小船渡河问题.
知识储备区
一、1.实际运动
2.相互替代 合成 平行四边形
3.相互替代 平行四边形
二、合成 分解
学习探究区
一、位移和速度的合成与分解
二、小船渡河问题
三、关联物体速度的分解
一、位移和速度的合成与分解
学习·探究区
问题设计
1.如图所示,小明由码头A出发,准备送一批货物到达河对岸的码头B.他驾船时始终保持船头指向与河岸垂直,但小明没有到达正对岸的码头B,而是到达下游的C处,此过程中小船参与了几个运动?
v水
v船
v合
答案 参与了两个运动,即船垂直河岸的运动和随水向下的漂流运动
一、位移和速度的合成与分解
学习·探究区
问题设计
2.如图所示,在一张白纸上,让铅笔沿尺边横向移动的同时让直尺沿纵向移动,研究笔尖的横向位移、纵向位移与笔尖的实际位移三者有什么关系?
x1
x2
v合
答案 满足平行四边形定则
一、位移和速度的合成与分解
2. 合运动与分运动的关系:
(1)等时性:合运动与分运动经历的 相等,即同时开始,同时进行,同时停止.
学习·探究区
(2)独立性:一个物体同时参与了几个分运动,各分运动 、互不影响,因此在研究某个分运动时,就可以不考虑其他分运动,就像其他分运动不存在一样.
(3)等效性:各分运动的相应参量叠加起来与 的参量相同.
1.位移和速度的合成与分解都遵循 定则.
平行四边形
时间
独立进行
合运动
分析两个直线运动的合运动的性质时,应先根据平行四边形定则,求出合运动的合初速度v0和合加速度a,然后进行判断.
(1)判断是否做匀变速运动
学习·探究区
①若a=0时,物体沿合初速度v0的方向做匀速直线运动.
②若a≠0且a恒定时,做匀变速运动.
③若a≠0且a变化时,做非匀变速运动.
(2)判断轨迹的曲直
①若a与速度共线,则做直线运动.
②若a与速度不共线,则做曲线运动.
3. 合运动性质的判断
一、位移和速度的合成与分解
返回
二、小船渡河问题
小船渡河问题一般有渡河时间最短和航程最短两类问题:
1.关于最短时间,可根据运动等时性原理由船对静水的分运动时间来求解,由于河宽一定,当船对静水速度v1垂直河岸时,如图所示,垂直河岸方向的分速度最大,所以必有
学习·探究区
v2
v1
v合
二、小船渡河问题
学习·探究区
小船渡河问题一般有渡河时间最短和航程最短两类问题:
2.关于最短航程,一般考察水流速度v2小于船对静水速度v1的情况较多,此种情况船的最短航程就等于河宽d,此时船头指向应与上游河岸成θ角(如图所示),且cos θ= ;若v2>v1,则最短航程s= d,此时船头指向应与上游河岸成θ′角,且cos θ′= .
v2
v1
v合
返回
三、关联物体的速度分解问题
绳、杆等连接的两个物体在运动过程中,其速度通常是不一样的,但两者的速度是有联系的(一般两个物体沿绳或杆方向的速度大小相等),我们称之为“关联”速度.解决此类问题的一般步骤如下:
学习·探究区
第一步:先确定合运动,物体的实际运动就是合运动;
第二步:确定合运动的两个实际作用效果:
一是沿牵引方向的平动效果,改变速度的大小;
二是沿垂直于牵引方向的转动效果,改变速度的方向;
第三步:按平行四边形定则进行分解,作好运动矢量图;
第四步:根据沿绳(或杆)牵引方向的速度相等列方程.
三、关联物体的速度分解问题
例如,小车通过跨过滑轮的绳牵引小船B,某一时刻绳与水平方向的夹角为θ,如图所示.
学习·探究区
小船速度vB有两个效果(两个分运动)
一是沿绳方向的平动,
二是垂直绳方向的转动.
将vB沿着这两个方向分解,
v1=vBcos θ=vA
v2=vBsin θ
返回
一、运动的合成与分解
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:ax=0
(1)物体所受的合力:
匀加:
沿y轴正方向
解析
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:vx0=3ms
?
(2)物体的初速度为:
匀加:
沿x轴正方向
解析
一、运动的合成与分解
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:vx=3ms
?
(3)合速度:
匀加:
解析
一、运动的合成与分解
典例精析
例1 质量m=2 kg的物体在光滑水平面上运动,其分速度vx和vy随时间变化的图线如图(a)、(b)所示,求:
(1)物体所受的合力;
(2)物体的初速度;
(3)t=8 s时物体的速度;
(4)t=4 s内物体的位移.
匀速:x=12 m
(4)合位移:
匀加:
解析
返回
典例精析
一、运动的合成与分解
二、小船渡河问题
例2 已知某船在静水中的速率为v1=4 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,河水的流动速度为v2=3 m/s,方向与河岸平行.试分析:
(1)欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移是多大?
(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
解析:
(1)船头垂直对岸,渡河时间最短
船的位移为
到达对岸A处,顺水漂流的位移
x=v2tmin=3×25 m=75 m
返回
典例精析
二、小船渡河问题
例2 已知某船在静水中的速率为v1=4 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,河水的流动速度为v2=3 m/s,方向与河岸平行.试分析:
(1)欲使船以最短时间渡过河去,船的航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移是多大?
(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
(2)v1>v2,合速度与河岸垂直,航行距离最短.
设船头与河岸成θ角
船的合速度为
返回
典例精析
例3 如图所示,做匀速直线运动的汽车A通过一根绕过定滑轮的长绳吊起一重物B,设重物和汽车的速度的大小分别为vB、vA,则( )
A.vA=vB B.vA<vB
C.vA>vB D.重物B的速度逐渐增大
三、关联物体速度的分解
两个运动效果
一是使绳子伸长
二是使绳子转动
归属于绳子头问题:
实际速度为合速度
关联
vB=vA cosα
CD
返回
典例精析
自我检测区
1
2
3
4
1.(合运动与分运动的关系)对于两个分运动的合运动,下列说法正确的是( )
A.合运动的速度大小等于两个分运
动的速度大小之和
B.合运动的速度一定大于某一个分
运动的速度
C.合运动的方向就是物体实际运动
的方向
D.由两个分速度的大小就可以确定
合速度的大小
C
1
2
3
4
可能大于分运动,
也可能小于分运动
还需要知道分运动的方向
解析
2.(合运动运动性质的判断)关于运动的合成,下列说法中正确的是( )
A.两个直线运动的合运动,一定是直线
运动
B.两个直线运动的合运动,可能是曲线
运动
C.两个互成角度的匀速直线运动的合运
动,一定是匀速直线运动
D.两个互成角度的匀加速直线运动的合
运动,一定是匀加速直线运动
a合与v合
方向
取决于
共线
直线运动
不共线
曲线运动
a1=0
a2=0
a合=0
v 1恒定
v 2恒定
v 合恒定
匀速
直线
v 2
v 1
v 合
a 1
a 合
a2
匀加速直线
v 2
v 1
v 合
a 1
a 合
a2
匀加速曲线
BC
解析
1
2
3
4
3.(关联物体速度的分解)如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动.则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
A.F不变、v不变
B.F增大、v不变
C.F增大、v增大
D.F增大、v减小
Fcos θ=mg
受力分析
θ
受力平衡
θ
cos θ
F
解析
1
2
3
4
3.(关联物体速度的分解)如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动.则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
A.F不变、v不变
B.F增大、v不变
C.F增大、v增大
D.F增大、v减小
v=v物cos θ
运动分析
θ
θ
cos θ
v
分解速度
解析
1
2
3
4
4.小船在200 m宽的河中横渡,水流速度是2 m/s,小船在静水中的航速是4 m/s.求:
(1)要使小船渡河耗时最少,应如何航行?最短时间为多少?
(2)要使小船航程最短,应如何航行
?最短航程为多少?
垂直河岸
分速度最大
(1)船头朝正对岸耗时最少
v水
v船
v合
(2)v合垂直对岸,航程最短为d
解得
解析
v水
v船
v合
1
2
3
4
