2020-2021苏科版九年级数学上册:2.5直线与圆的位置关系(4)同步巩固训练卷(word版,含答案)
文档属性
| 名称 | 2020-2021苏科版九年级数学上册:2.5直线与圆的位置关系(4)同步巩固训练卷(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 461.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 16:00:59 | ||
图片预览


文档简介
2020-2021苏科版九年级数学上册2.5直线与圆的位置关系(4)同步巩固训练卷
一、选择题
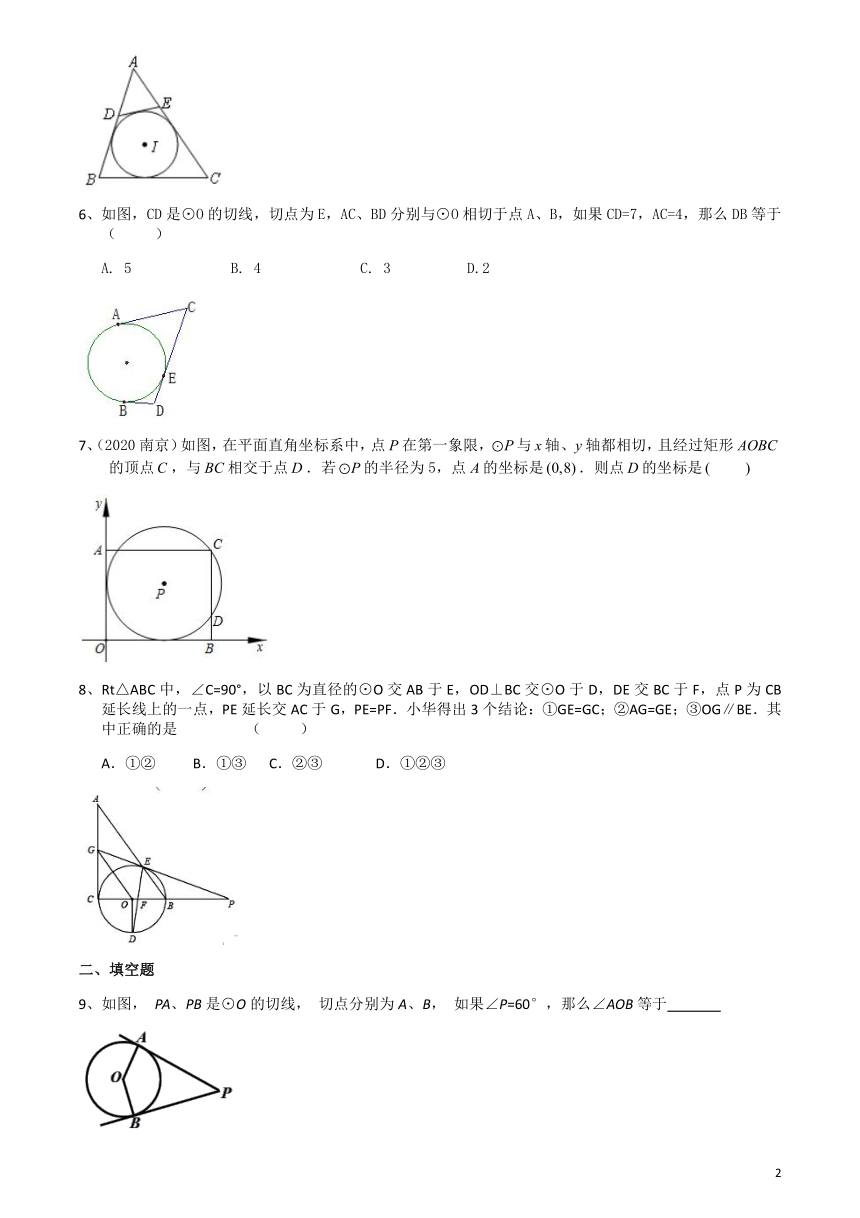
1、如图,PQ、PR、AB是的切线,切点分别为Q、R、S,若,则等于( )
A. 40? B. 50? C. 60? D. 70?
(1题) (2题)
2、(2020?永州)如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆; ④M是△AOP外接圆的圆心.
其中正确说法的个数是( )
A.1 B.2 C.3 D.4
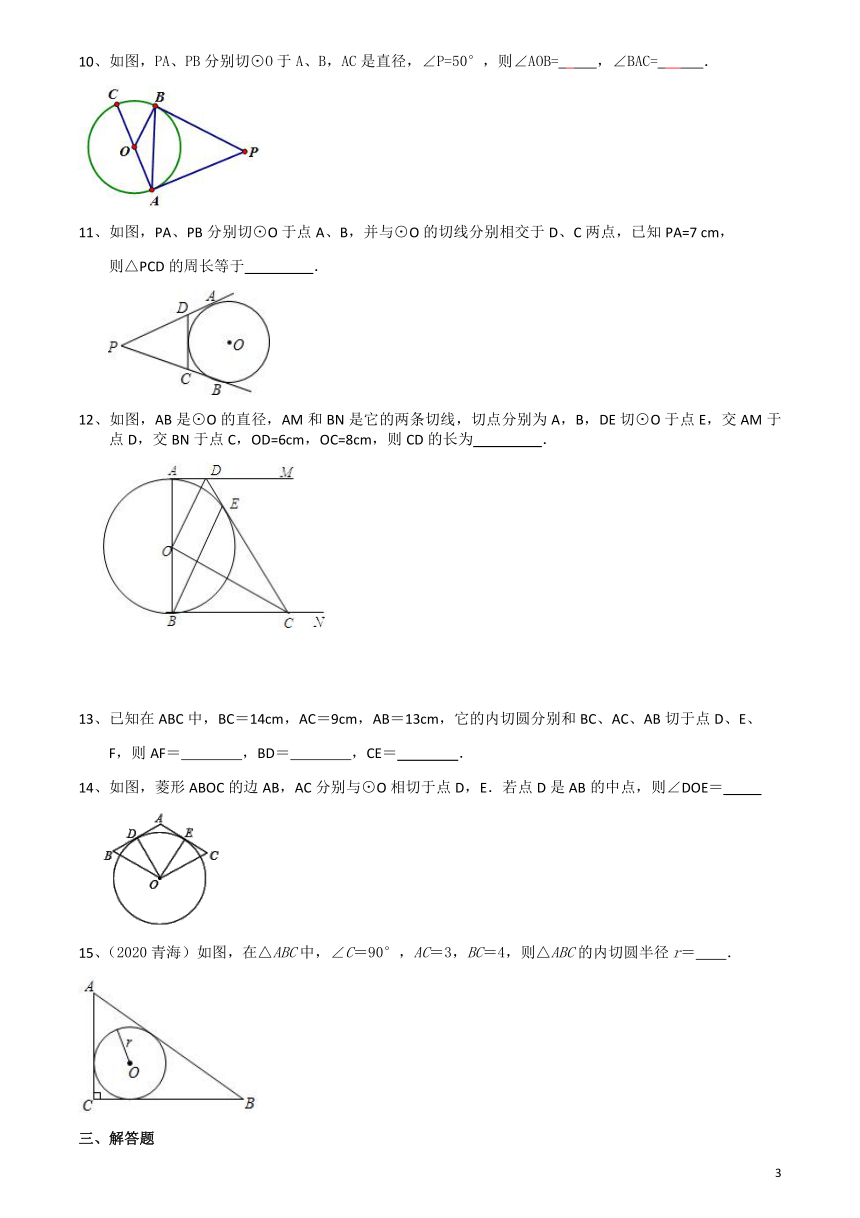
3、在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为 ( )
A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9 C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5
4、(2020?通辽)如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C=( )
A.108° B.72° C.54° D.36°
5、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若 的周长为21,边的长为6,则的周长为( )
A.15 B.9 C.8 D.7.5
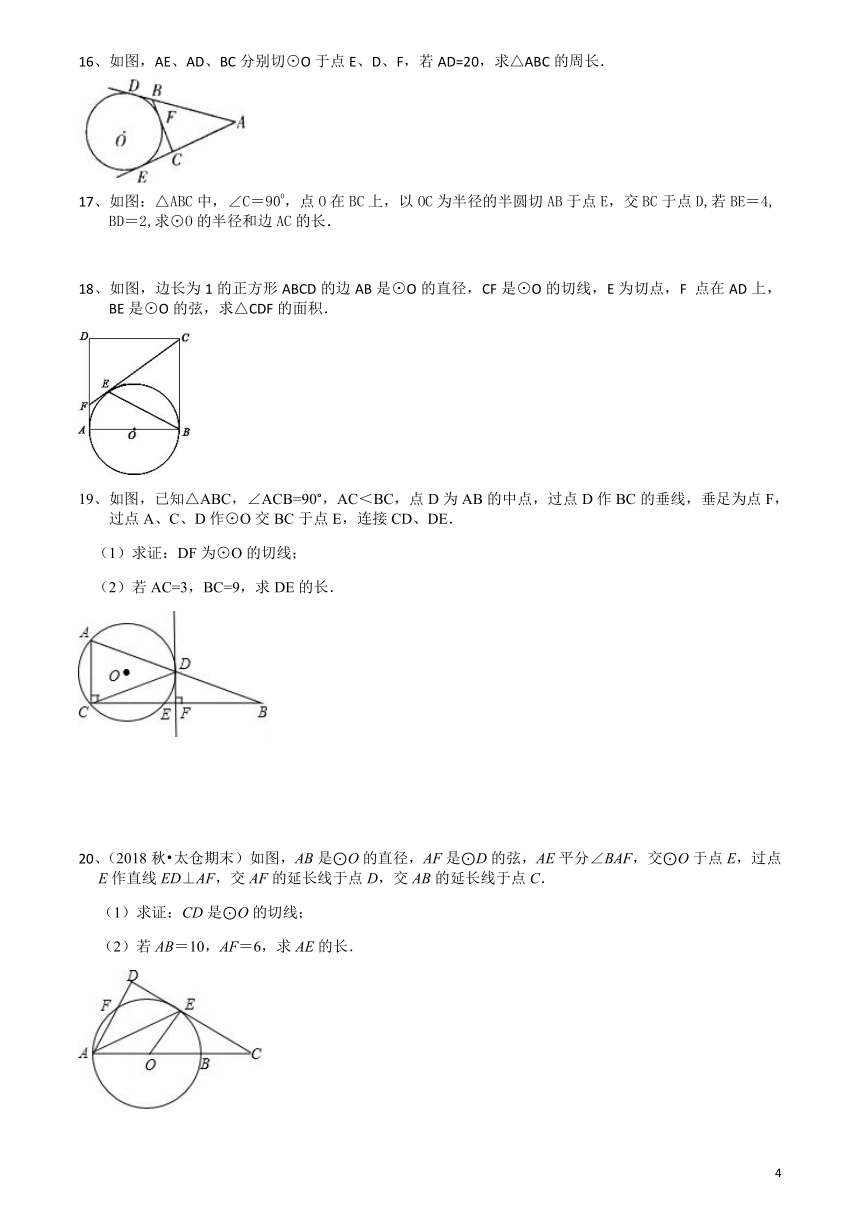
6、如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B,如果CD=7,AC=4,那么DB等于 ( )
A. 5 B. 4 C. 3 D.2
7、(2020南京)如图,在平面直角坐标系中,点在第一象限,与轴、轴都相切,且经过矩形 的顶点,与相交于点.若的半径为5,点的坐标是.则点的坐标是
8、Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF.小华得出3个结论:①GE=GC;②AG=GE;③OG∥BE.其中正确的是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9、如图, PA、PB是⊙O的切线, 切点分别为A、B, 如果∠P=60°,那么∠AOB等于
10、如图,PA、PB分别切⊙O于A、B,AC是直径,∠P=50°,则∠AOB= ,∠BAC= .
11、如图,PA、PB分别切⊙O于点A、B,并与⊙O的切线分别相交于D、C两点,已知PA=7 cm,
则△PCD的周长等于 .
12、如图,AB是⊙O的直径,AM和BN是它的两条切线,切点分别为A,B,DE切⊙O于点E,交AM于点D,交BN于点C,OD=6cm,OC=8cm,则CD的长为 .
13、已知在ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、
F,则AF= ,BD= ,CE= .
14、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=
15、(2020青海)如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= .
三、解答题
16、如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
17、如图:△ABC中,∠C=900,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,若BE=4,
BD=2,求⊙O的半径和边AC的长.
18、如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F 点在AD上,BE是⊙O的弦,求△CDF的面积.
19、如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE.
(1)求证:DF为⊙O的切线;
(2)若AC=3,BC=9,求DE的长.
20、(2018秋?太仓期末)如图,AB是⊙O的直径,AF是⊙D的弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)若AB=10,AF=6,求AE的长.
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
2020-2021苏科版九年级数学上册2.5直线与圆的位置关系(4)同步巩固训练卷(答案)
一、选择题
1、如图,PQ、PR、AB是的切线,切点分别为Q、R、S,若,则等于( D )
A. 40? B. 50? C. 60? D. 70?
2、(2020?永州)如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆; ④M是△AOP外接圆的圆心.
其中正确说法的个数是( C )
A.1 B.2 C.3 D.4
3、在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为 ( A )
A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9 C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5
4、(2020?通辽)如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C=( C )
A.108° B.72° C.54° D.36°
5、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若 的周长为21,边的长为6,则的周长为( B )
A.15 B.9 C.8 D.7.5
6、如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B,如果CD=7,AC=4,那么DB等于 ( C )
A. 5 B. 4 C. 3 D.2
7、(2020南京)如图,在平面直角坐标系中,点在第一象限,与轴、轴都相切,且经过矩形 的顶点,与相交于点.若的半径为5,点的坐标是.则点的坐标是 A
8、Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF.小华得出3个结论:①GE=GC;②AG=GE;③OG∥BE.其中正确的是 ( D )
A.①② B.①③ C.②③ D.①②③
二、填空题
9、如图, PA、PB是⊙O的切线, 切点分别为A、B, 如果∠P=60°,那么∠AOB等于 120°
10、如图,PA、PB分别切⊙O于A、B,AC是直径,∠P=50°,则∠AOB= 130? ,∠BAC= 25? .
11、如图,PA、PB分别切⊙O于点A、B,并与⊙O的切线分别相交于D、C两点,已知PA=7 cm,
则△PCD的周长等于 14 cm .
12、如图,AB是⊙O的直径,AM和BN是它的两条切线,切点分别为A,B,DE切⊙O于点E,交AM于点D,交BN于点C,OD=6cm,OC=8cm,则CD的长为 10 cm .
13、已知在ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、
F,则AF= 4 ,BD= 9 ,CE= 5 .
14、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= 60° .
15、(2020青海)如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= 1 .
三、解答题
16、如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
【答案】解:∵,AE、AD、BC分别切⊙O于点E、D、F, ∴AD=AE=20,DB=BF,FC=EC
∵△ABC的周长为:AB+BF+CF+AC
∴△ABC的周长为:AB+DB+CE+AC=AD+AE=20+20=40.
17、如图:△ABC中,∠C=900,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,若BE=4,
BD=2,求⊙O的半径和边AC的长.
R=3;AC=6
18、如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F 点在AD上,BE是⊙O的弦,求△CDF的面积.
19、如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE.
(1)求证:DF为⊙O的切线;
(2)若AC=3,BC=9,求DE的长.
【解答】(1)证明:连接DO并延长交AC于M,如图1所示:
∵∠ACB=90°,AC<BC,点D为AB的中点,∴CD=AB=AD,∴,∴DM⊥AC,∴DM∥BC,
∵DF⊥BC,∴DF⊥DO,∴DF为⊙O的切线;
(2)解:由(1)得:AC∥DF,
∵点D为AB的中点,∴DF=AC=1.5,CF=BF=BC=4.5,
作ON⊥CE于N,连接OA,如图2所示:则CN=EN=CE,AM=CM=ON=DF=1.5,
设⊙O的半径为r,在△AOM中,由勾股定理得:r2+(4.5﹣r)2=r2,解得:r=2.5,
∴CN=EN=OM=4.5﹣2.5=2,∴CE=4,∴EF=4.5﹣4=0.5,
∴DE===.
20、(2018秋?太仓市期末)如图,AB是⊙O的直径,AF是⊙D的弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)若AB=10,AF=6,求AE的长.
【解答】(1)证明:∵AE平分∠DAC,∴∠CAE=∠DAE.
∵OA=OE,∴∠OEA=∠OAE.∴∠DAE=∠AEO,.∴AD∥OE.
∵AD⊥CD,∴OE⊥CD.∴CD是⊙O的切线.
(2)解:连接BF交OE于K.
∵AB是直径,∴∠AFB=90°,
∵AB=10,AF=6,∴BF==8,
∵OE∥AD,∴∠OKB=∠AFB=90°,∴OE⊥BF,∴FK=BK=4,
∵OA=OB,KF=KB,∴OK=AF=3,∴EK=OE﹣OK=2,
∵∠D=∠DFK=∠FKE=90°,∴四边形DFKE是矩形,
∴DE=KF=4,DF=EK=2,∴AD=AF+DF=8,
在Rt△ADE中,AE===4.
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
【答案】 (1)BC所在直线与小圆相切.理由如下:
过圆心O作OE⊥BC,垂足为E;∵AC是小圆的切线,AB经过圆心O,∴OA⊥AC;
又∵CO平分∠ACB,OE⊥BC,∴OE=OA,∴BC所在直线是小圆的切线.
(2)AC+AD=BC.理由如下:
连接OD.∵AC切小圆O于点A,BC切小圆O于点E,∴CE=CA;
∵在Rt△OAD与Rt△OEB中,,∴Rt△OAD≌Rt△OEB(HL),∴EB=AD;
∵BC=CE+EB,∴BC=AC+AD.
(3)∵∠BAC=90°,AB=8cm,BC=10cm,∴AC=6cm;∵BC=AC+AD,
∴AD=BC﹣AC=4cm,
∵圆环的面积为:S=π(OD)2﹣π(OA)2=π(OD2﹣OA2),
又∵OD2﹣OA2=AD2,∴S=42π=16π(cm2).
一、选择题
1、如图,PQ、PR、AB是的切线,切点分别为Q、R、S,若,则等于( )
A. 40? B. 50? C. 60? D. 70?
(1题) (2题)
2、(2020?永州)如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆; ④M是△AOP外接圆的圆心.
其中正确说法的个数是( )
A.1 B.2 C.3 D.4
3、在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为 ( )
A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9 C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5
4、(2020?通辽)如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C=( )
A.108° B.72° C.54° D.36°
5、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若 的周长为21,边的长为6,则的周长为( )
A.15 B.9 C.8 D.7.5
6、如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B,如果CD=7,AC=4,那么DB等于 ( )
A. 5 B. 4 C. 3 D.2
7、(2020南京)如图,在平面直角坐标系中,点在第一象限,与轴、轴都相切,且经过矩形 的顶点,与相交于点.若的半径为5,点的坐标是.则点的坐标是
8、Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF.小华得出3个结论:①GE=GC;②AG=GE;③OG∥BE.其中正确的是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9、如图, PA、PB是⊙O的切线, 切点分别为A、B, 如果∠P=60°,那么∠AOB等于
10、如图,PA、PB分别切⊙O于A、B,AC是直径,∠P=50°,则∠AOB= ,∠BAC= .
11、如图,PA、PB分别切⊙O于点A、B,并与⊙O的切线分别相交于D、C两点,已知PA=7 cm,
则△PCD的周长等于 .
12、如图,AB是⊙O的直径,AM和BN是它的两条切线,切点分别为A,B,DE切⊙O于点E,交AM于点D,交BN于点C,OD=6cm,OC=8cm,则CD的长为 .
13、已知在ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、
F,则AF= ,BD= ,CE= .
14、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=
15、(2020青海)如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= .
三、解答题
16、如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
17、如图:△ABC中,∠C=900,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,若BE=4,
BD=2,求⊙O的半径和边AC的长.
18、如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F 点在AD上,BE是⊙O的弦,求△CDF的面积.
19、如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE.
(1)求证:DF为⊙O的切线;
(2)若AC=3,BC=9,求DE的长.
20、(2018秋?太仓期末)如图,AB是⊙O的直径,AF是⊙D的弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)若AB=10,AF=6,求AE的长.
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
2020-2021苏科版九年级数学上册2.5直线与圆的位置关系(4)同步巩固训练卷(答案)
一、选择题
1、如图,PQ、PR、AB是的切线,切点分别为Q、R、S,若,则等于( D )
A. 40? B. 50? C. 60? D. 70?
2、(2020?永州)如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆; ④M是△AOP外接圆的圆心.
其中正确说法的个数是( C )
A.1 B.2 C.3 D.4
3、在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为 ( A )
A.AF=4,BD=9,CE=5 B.AF=4,BD=5,CE=9 C.AF=5,BD=4,CE=9 D.AF=9,BD=4,CE=5
4、(2020?通辽)如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,则∠C=( C )
A.108° B.72° C.54° D.36°
5、如图,⊙I为的内切圆,点分别为边上的点,且为⊙I的切线,若 的周长为21,边的长为6,则的周长为( B )
A.15 B.9 C.8 D.7.5
6、如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B,如果CD=7,AC=4,那么DB等于 ( C )
A. 5 B. 4 C. 3 D.2
7、(2020南京)如图,在平面直角坐标系中,点在第一象限,与轴、轴都相切,且经过矩形 的顶点,与相交于点.若的半径为5,点的坐标是.则点的坐标是 A
8、Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF.小华得出3个结论:①GE=GC;②AG=GE;③OG∥BE.其中正确的是 ( D )
A.①② B.①③ C.②③ D.①②③
二、填空题
9、如图, PA、PB是⊙O的切线, 切点分别为A、B, 如果∠P=60°,那么∠AOB等于 120°
10、如图,PA、PB分别切⊙O于A、B,AC是直径,∠P=50°,则∠AOB= 130? ,∠BAC= 25? .
11、如图,PA、PB分别切⊙O于点A、B,并与⊙O的切线分别相交于D、C两点,已知PA=7 cm,
则△PCD的周长等于 14 cm .
12、如图,AB是⊙O的直径,AM和BN是它的两条切线,切点分别为A,B,DE切⊙O于点E,交AM于点D,交BN于点C,OD=6cm,OC=8cm,则CD的长为 10 cm .
13、已知在ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、
F,则AF= 4 ,BD= 9 ,CE= 5 .
14、如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE= 60° .
15、(2020青海)如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= 1 .
三、解答题
16、如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.
【答案】解:∵,AE、AD、BC分别切⊙O于点E、D、F, ∴AD=AE=20,DB=BF,FC=EC
∵△ABC的周长为:AB+BF+CF+AC
∴△ABC的周长为:AB+DB+CE+AC=AD+AE=20+20=40.
17、如图:△ABC中,∠C=900,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,若BE=4,
BD=2,求⊙O的半径和边AC的长.
R=3;AC=6
18、如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F 点在AD上,BE是⊙O的弦,求△CDF的面积.
19、如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作⊙O交BC于点E,连接CD、DE.
(1)求证:DF为⊙O的切线;
(2)若AC=3,BC=9,求DE的长.
【解答】(1)证明:连接DO并延长交AC于M,如图1所示:
∵∠ACB=90°,AC<BC,点D为AB的中点,∴CD=AB=AD,∴,∴DM⊥AC,∴DM∥BC,
∵DF⊥BC,∴DF⊥DO,∴DF为⊙O的切线;
(2)解:由(1)得:AC∥DF,
∵点D为AB的中点,∴DF=AC=1.5,CF=BF=BC=4.5,
作ON⊥CE于N,连接OA,如图2所示:则CN=EN=CE,AM=CM=ON=DF=1.5,
设⊙O的半径为r,在△AOM中,由勾股定理得:r2+(4.5﹣r)2=r2,解得:r=2.5,
∴CN=EN=OM=4.5﹣2.5=2,∴CE=4,∴EF=4.5﹣4=0.5,
∴DE===.
20、(2018秋?太仓市期末)如图,AB是⊙O的直径,AF是⊙D的弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)若AB=10,AF=6,求AE的长.
【解答】(1)证明:∵AE平分∠DAC,∴∠CAE=∠DAE.
∵OA=OE,∴∠OEA=∠OAE.∴∠DAE=∠AEO,.∴AD∥OE.
∵AD⊥CD,∴OE⊥CD.∴CD是⊙O的切线.
(2)解:连接BF交OE于K.
∵AB是直径,∴∠AFB=90°,
∵AB=10,AF=6,∴BF==8,
∵OE∥AD,∴∠OKB=∠AFB=90°,∴OE⊥BF,∴FK=BK=4,
∵OA=OB,KF=KB,∴OK=AF=3,∴EK=OE﹣OK=2,
∵∠D=∠DFK=∠FKE=90°,∴四边形DFKE是矩形,
∴DE=KF=4,DF=EK=2,∴AD=AF+DF=8,
在Rt△ADE中,AE===4.
21、如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.
【答案】 (1)BC所在直线与小圆相切.理由如下:
过圆心O作OE⊥BC,垂足为E;∵AC是小圆的切线,AB经过圆心O,∴OA⊥AC;
又∵CO平分∠ACB,OE⊥BC,∴OE=OA,∴BC所在直线是小圆的切线.
(2)AC+AD=BC.理由如下:
连接OD.∵AC切小圆O于点A,BC切小圆O于点E,∴CE=CA;
∵在Rt△OAD与Rt△OEB中,,∴Rt△OAD≌Rt△OEB(HL),∴EB=AD;
∵BC=CE+EB,∴BC=AC+AD.
(3)∵∠BAC=90°,AB=8cm,BC=10cm,∴AC=6cm;∵BC=AC+AD,
∴AD=BC﹣AC=4cm,
∵圆环的面积为:S=π(OD)2﹣π(OA)2=π(OD2﹣OA2),
又∵OD2﹣OA2=AD2,∴S=42π=16π(cm2).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
