五年级上册数学课件-6.2 三角形 的面积冀教版 (共32张PPT)
文档属性
| 名称 | 五年级上册数学课件-6.2 三角形 的面积冀教版 (共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 20:46:20 | ||
图片预览





文档简介
(共32张PPT)
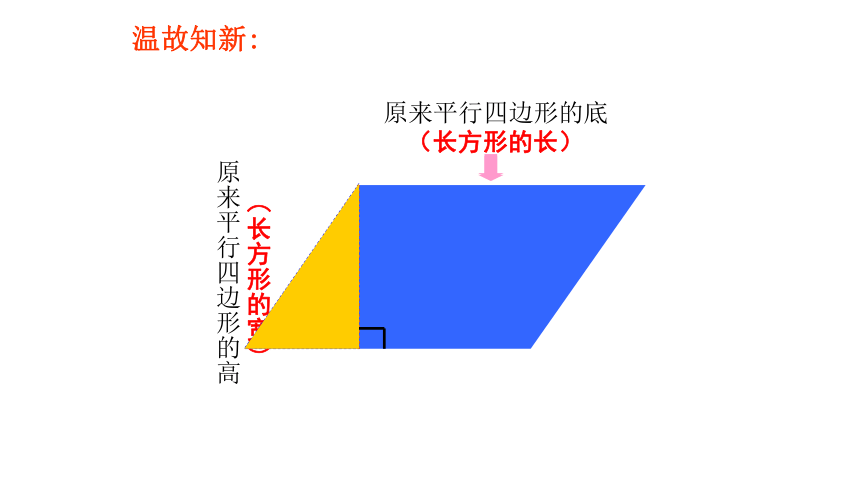
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
温故知新:
长方形的面积
=
长
×
宽
平行四边形的面积
=
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
温故知新:
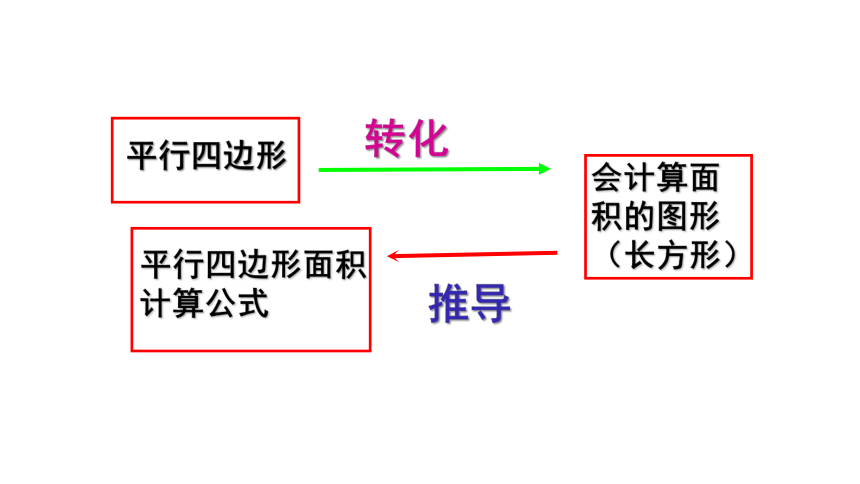
转化
会计算面积的图形(长方形)
推导
平行四边形
平行四边形面积计算公式
1.如何将三角形转化成我们学过的图形?
2.三角形与拼成的图形之间有什么关系?
想一想:
1.四人小组合作(分配任务)。
2.填写学习单
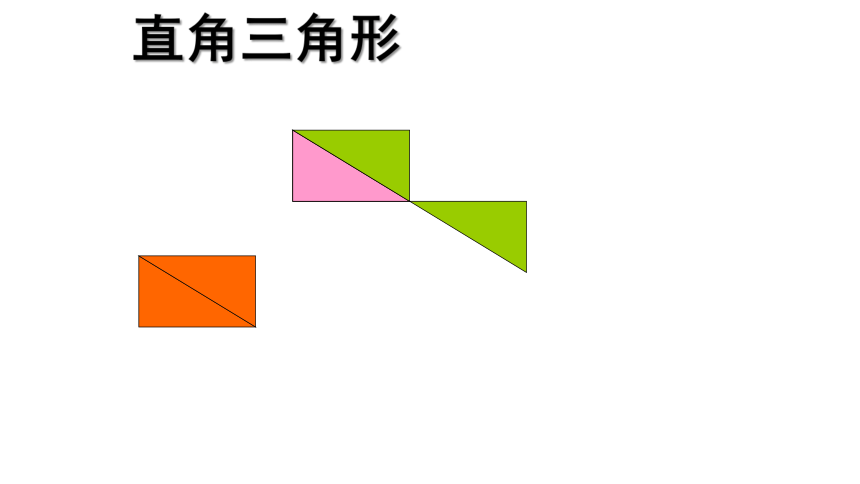
直角三角形
直角三角形
直角三角形
两个完全一样的直角三角形,可以拼成一个平行四边形。
锐角三角形
锐角三角形
两个完全一样的锐角三角形,可以拼成一个平行四边形。
锐角三角形
钝角三角形
钝角三角形
钝角三角形
两个完全一样的钝角三角形,可以拼成一个平行四边形。
直角三角形
两个完全一样的直角三角形,可以拼成一个平行四边形。
直角三角形
结论2:锐角三角形的面积是拼成的平行四边形面积的一半。
结论1:直角三角形的面积是拼成的平行四边形面积的一半。
结论3:钝角三角形的面积是拼成的平行四边形面积的一半。
三角形的面积是拼成的平行四边形面积的一半。
三角形的面积=平行四边形的面积÷2
三角形的面积=底×高÷2
S=ah÷2
三角形的面积是与它同底同高的平行四边形面积的一半。
每个三角形的面积等于与它等底等高的平行四边形面积的一半
平行四边形的面积
=
底
X
高
三角形的面积=底X高?2
平行四边形的底和高就是三角形的底和高
S=ah?2
我国古代数学家刘徽利用出入相补的原理来计算平面图形的面积。
出入相补就是在图形面积保持不变的前提下把一个图形经过分割、移补,从而计算出图形的面积。
请欣赏
在名著《九章算术》中说:
“圭田术曰半广以乘正从(zòng)
。”
圭田指三角形的田地,术是指面积的计算方法,
半广指三角形底的一半,正从是指三角形的高。
三角形的面积=底÷2×高
“亦可半正从(zòng)以乘广。”
三角形的面积=高÷2×底
高÷2×底
底÷2×高
底×高÷2
底×高÷2
三角形的面积公式
计算:你们能算出这三个三角形的面积吗?
6cm
8cm
7cm
4cm
1.5cm
1cm
①
②
③
4cm
6cm
判断:
①三角形的底是6cm,底边上的高是3cm,
面积是18cm2。(
)
②两个完全一样的锐角三角形可以拼成一个
平行四边形。
(
)
×
√
S△=ah÷2
③三角形的面积总是平行四边形面积的一半。(
)
×
乙
甲
1)下图是两个完全相同的平行四边形,
甲的面积和乙的面积相比(
)
①S甲>S乙
②S甲<S乙
③
S甲=S乙
①
选择:
选择:
2)长方形ABCD中,△EBC的面积和△FBC
的面积相比(
)
①
△EBC的面积大
②
△FBC的面积大
③一样大
③
A
B
E
F
D
C
M
N
O
选择:
2)长方形ABCD中,△EBO的面积和△FCO
的面积相比(
)
①
△EBO的面积大
②
△FCO的面积大
③一样大
③
A
B
E
F
D
C
O
2)长方形ABCD中,△ABC的面积和△EBC、
△FBC的面积相比(
)
A
B
E
F
D
C
O
一样大
2)长方形ABCD中,△DBC的面积和△EBC、
△FBC的面积相比(
)
A
B
E
F
D
C
O
一样大
你有什么收获?
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
温故知新:
长方形的面积
=
长
×
宽
平行四边形的面积
=
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
温故知新:
转化
会计算面积的图形(长方形)
推导
平行四边形
平行四边形面积计算公式
1.如何将三角形转化成我们学过的图形?
2.三角形与拼成的图形之间有什么关系?
想一想:
1.四人小组合作(分配任务)。
2.填写学习单
直角三角形
直角三角形
直角三角形
两个完全一样的直角三角形,可以拼成一个平行四边形。
锐角三角形
锐角三角形
两个完全一样的锐角三角形,可以拼成一个平行四边形。
锐角三角形
钝角三角形
钝角三角形
钝角三角形
两个完全一样的钝角三角形,可以拼成一个平行四边形。
直角三角形
两个完全一样的直角三角形,可以拼成一个平行四边形。
直角三角形
结论2:锐角三角形的面积是拼成的平行四边形面积的一半。
结论1:直角三角形的面积是拼成的平行四边形面积的一半。
结论3:钝角三角形的面积是拼成的平行四边形面积的一半。
三角形的面积是拼成的平行四边形面积的一半。
三角形的面积=平行四边形的面积÷2
三角形的面积=底×高÷2
S=ah÷2
三角形的面积是与它同底同高的平行四边形面积的一半。
每个三角形的面积等于与它等底等高的平行四边形面积的一半
平行四边形的面积
=
底
X
高
三角形的面积=底X高?2
平行四边形的底和高就是三角形的底和高
S=ah?2
我国古代数学家刘徽利用出入相补的原理来计算平面图形的面积。
出入相补就是在图形面积保持不变的前提下把一个图形经过分割、移补,从而计算出图形的面积。
请欣赏
在名著《九章算术》中说:
“圭田术曰半广以乘正从(zòng)
。”
圭田指三角形的田地,术是指面积的计算方法,
半广指三角形底的一半,正从是指三角形的高。
三角形的面积=底÷2×高
“亦可半正从(zòng)以乘广。”
三角形的面积=高÷2×底
高÷2×底
底÷2×高
底×高÷2
底×高÷2
三角形的面积公式
计算:你们能算出这三个三角形的面积吗?
6cm
8cm
7cm
4cm
1.5cm
1cm
①
②
③
4cm
6cm
判断:
①三角形的底是6cm,底边上的高是3cm,
面积是18cm2。(
)
②两个完全一样的锐角三角形可以拼成一个
平行四边形。
(
)
×
√
S△=ah÷2
③三角形的面积总是平行四边形面积的一半。(
)
×
乙
甲
1)下图是两个完全相同的平行四边形,
甲的面积和乙的面积相比(
)
①S甲>S乙
②S甲<S乙
③
S甲=S乙
①
选择:
选择:
2)长方形ABCD中,△EBC的面积和△FBC
的面积相比(
)
①
△EBC的面积大
②
△FBC的面积大
③一样大
③
A
B
E
F
D
C
M
N
O
选择:
2)长方形ABCD中,△EBO的面积和△FCO
的面积相比(
)
①
△EBO的面积大
②
△FCO的面积大
③一样大
③
A
B
E
F
D
C
O
2)长方形ABCD中,△ABC的面积和△EBC、
△FBC的面积相比(
)
A
B
E
F
D
C
O
一样大
2)长方形ABCD中,△DBC的面积和△EBC、
△FBC的面积相比(
)
A
B
E
F
D
C
O
一样大
你有什么收获?
