题型分类学案:解三角形(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
题型分类:解三角形
要点一、三角形中的边与角之间的关系
约定:的三个内角、、所对应的三边分别为、、.
1.边的关系:
(1) 两边之和大于第三边:,,;
两边之差小于第三边:,,;
(2) 勾股定理:中,.
2.角的关系:
中,,=
(1)互补关系:
(2)互余关系:
3.直角三角形中的边与角之间的关系
中,(如图),有:
,
.
要点二、正弦定理、余弦定理
1.正弦定理:在—个三角形中,各边和它所对角的正弦的比相等.即:
(为的外接圆半径)
2. 余弦定理:三角形任意一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。即:
要点诠释:
(1)正弦定理适合于任何三角形;每个等式可视为一个方程:知三求一.
(2)利用正弦定理可以解决下列两类三角形的问题:
①已知两个角及任意—边,求其他两边和另一角;
②已知两边和其中—边的对角,求其他两个角及另一边.
(3)利用余弦定理可以解决下列两类三角形的问题:
①已知三角形的两条边及夹角,求第三条边及其他两个角;
②已知三角形的三条边,求其三个角.
(4) 利用余弦定理判断三角形形状:
①勾股定理是余弦定理的特殊情况,.
②在中,,所以为锐角;
若,,同理可得角、为锐角.
当,,都成立时,为锐角三角形.
③在中,若,
所以为钝角,则是钝角三角形.
同理:若,则是钝角三角形且为钝角;
若,则是钝角三角形且为钝角.
要点三、解斜三角形的类型
1.已知两角一边,用正弦定理,有解时,只有一解.
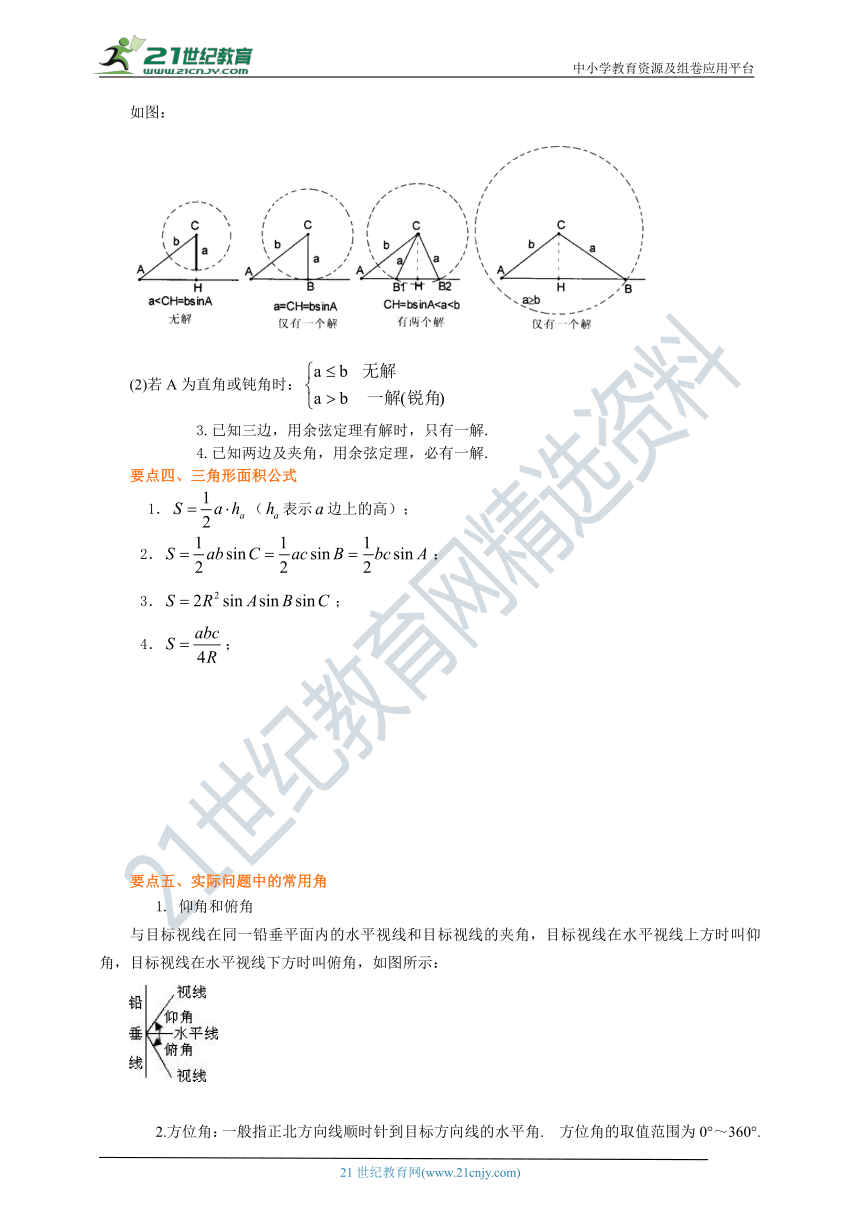
2.已知两边及其一边的对角,用正弦定理,有解的情况可分为以下情况,在中,已知和角时,解的情况如下:
(1)若A为锐角时:
如图:
(2)若A为直角或钝角时:
3.已知三边,用余弦定理有解时,只有一解.
4.已知两边及夹角,用余弦定理,必有一解.
要点四、三角形面积公式
1.(表示边上的高);
2.;
3.;
4.;
要点五、实际问题中的常用角
1. 仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角,如图所示:
2.方位角:一般指正北方向线顺时针到目标方向线的水平角. 方位角的取值范围为0°~360°.
如图,点的方位角是。
3. 坡角和坡度
坡面与地平面所成的角度,叫做坡角;坡面的铅直高度和水平宽度的比叫做坡度或者_??????_,常用字母i表示。坡比是坡角的正切值。
【典型考法1:角度变化】
例1.在△ABC中,若2cos Bsin A=sin C,则△ABC的形状一定是( ).
A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
答案 C
解析 ∵2cos Bsin A=sin C=sin(A+B),
∴sin Acos B-cos Asin B=0,
即sin(A-B)=0,∴A=B.
【变式1】△ABC中,若==,则△ABC的形状是_______.
答案 等边三角形
解析 ∵a=2Rsin A,b=2Rsin B,c=2Rsin C,
∴==,∴sin=sin=sin,
又∵A+B+C=π,∴++=.
∴==,∴A=B=C=.
【变式2】在锐角△ABC中,角A、B、C的对边分别为a、b、c.若+=6cos C,则+的值是______.
解析 由+=6cos C,得b2+a2=6abcos C.
化简整理得2(a2+b2)=3c2,将+切化弦,
得·=·
=·=.
根据正、余定理得=
===4.
【变式3】在△ABC中,若则△ABC的形状是______________.
答案:直角三角形;
【典型考法2:正余弦定理混用】
例2.在△ABC中,内角A、B、C的对边分别为a、b、c,已知b2=ac且cos B=
(1)求+的值;
(2)设·=,求a+c的值
解 (1)由cos B=,得sin B= =.
由b2=ac及正弦定理得sin2B=sin Asin C.
于是+=+ ==
===.
(2)由·=得ca·cos B=,由cos B=,可得ca=2,即b2=2.
由余弦定理b2=a2+c2-2ac·cos B,
得a2+c2=b2+2ac·cos B=5,∴(a+c)2=a2+c2+2ac=5+4=9,∴a+c=3.
【变式1】在△ABC中,若,则的值是_______.
答案:1;
【变式2】 在△ABC中,若,且,边上的高为,求角的大小与边的长
答案:解:
,联合
得,即
当时,
当时,
∴当时,
当时,_._
【变式3】在△ABC中,若则△ABC的形状是什么?
答案:解:
或,得或
所以△ABC是直角三角形.
【变式4】的内角所对的边分别为,已知,
(1)求;
(2)若,的面积为,求。
(答案)(1);
(2)。
(解析)
试题分析:利用三角形内角和定理可知,再利用诱导公式化简,利用降幂公式化简,结合求出;利用(1)中结论,利用勾股定理和面积公式求出,从而求出。
试题解析:(1)由题设及,,故。
上式两边平方,整理得,
解得(舍去),。
(2)由得,故。
又,则。
由余弦定理及得:
所以b=2。
【典型考法3:范围求值】
例3.△ABC的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
【答案】(1)B=60°;(2).
【解析】(1)由题设及正弦定理得.
因为sinA0,所以.
由,可得,故.
因为,故,因此B=60°.
(2)由题设及(1)知△ABC的面积.
由正弦定理得.
由于△ABC为锐角三角形,故0°因此,△ABC面积的取值范围是.
【变式1】△的内角,,的对边分别为,,,且满足,.
(1)求角的大小;
(2)求△周长的最大值.
解:(Ⅰ)∵,
由正弦定理,
得,
,即,
又∵,
∵,∴.
(Ⅱ)由(Ⅰ)可知
,
∴当时,周长最大
最大值为2+4=6,即周长最大值是6
【变式2】在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)证明:;
(Ⅱ)求的最小值.
【解析】(Ⅰ)由
得,
所以,由正弦定理,得.
(Ⅱ)由
.
所以的最小值为.
【典型考法4:图形分析】
例4.已知△ABC中,AB=BC,AC=2,点D在边AC上,且AD=2CD,
∠ABD=2∠CBD。
(1)求∠ABC的大小;
(2)求△ABC的面积。
【变式1】如图,在中,是边的中点,,.
(Ⅰ)求角的大小;
(Ⅱ)若,求的面积.
【解析】(Ⅰ)由,得,
由,得
又,
所以,
=,
又,所以.
(Ⅱ)解法一:由(Ⅰ)知,
在中,由正弦定理,得,
所以, .
因为是边的中点,所以,.
故 .
解法二:由(Ⅰ)知,在中,
由正弦定理,得,
所以, .
因为是边的中点,所以,
所以, .
【变式2】如图,在中, ,点在边上, , 为垂足.
(1)若的面积为,求的长;
(2)若,求角的大小.
【答案】(1) ;(2) .
【典型考法5:实际应用】
例5.如图所示,某镇有一块空地,其中,,.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖,其中,都在边上,且,挖出的泥土堆放在地带上形成假山,剩下的地带开设儿童游乐场.为安全起见,需在的周围安装防护网.
(1)当时,求防护网的总长度;
(2)为节省投入资金,人工湖的面积要尽可能小,问如何设计施工方案,可使的面积最小?最小面积是多少?
【答案】(1) ;(2)当时,最小值为.
、
【变式1】如图,一山顶有一信号塔(所在的直线与地平面垂直),在山脚处测得塔尖的仰角为,沿倾斜角为的山坡向上前进米后到达处,测得的仰角为.
(1)求的长;
(2)若, , , ,求信号塔的高度.
【答案】(1) ;(2) .
【解析】(1)在中, , , .由正弦定理, ;
(2)由(1)及条件知, , , , .
由正弦定理得
【变式2】如图所示,在海岸A处,发现北偏东45°方向,距A为()km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以km/h的速度追截走私船.此时走私船正以10km/h的速度从B处向北偏东30°方向逃窜,则缉私船沿什么方向能最快追上走私船?并求出所需要的时间.
【解析】设缉私船追上走私船需,则,.
由余弦定理,得
,
由正弦定理,得,
∴,而,
∴
∴,.
∴,即,∴
答:缉私船向东偏北方向,只需便能追上走私船.
.
_21?????????è?????(www.21cnjy.com)_
题型分类:解三角形
要点一、三角形中的边与角之间的关系
约定:的三个内角、、所对应的三边分别为、、.
1.边的关系:
(1) 两边之和大于第三边:,,;
两边之差小于第三边:,,;
(2) 勾股定理:中,.
2.角的关系:
中,,=
(1)互补关系:
(2)互余关系:
3.直角三角形中的边与角之间的关系
中,(如图),有:
,
.
要点二、正弦定理、余弦定理
1.正弦定理:在—个三角形中,各边和它所对角的正弦的比相等.即:
(为的外接圆半径)
2. 余弦定理:三角形任意一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。即:
要点诠释:
(1)正弦定理适合于任何三角形;每个等式可视为一个方程:知三求一.
(2)利用正弦定理可以解决下列两类三角形的问题:
①已知两个角及任意—边,求其他两边和另一角;
②已知两边和其中—边的对角,求其他两个角及另一边.
(3)利用余弦定理可以解决下列两类三角形的问题:
①已知三角形的两条边及夹角,求第三条边及其他两个角;
②已知三角形的三条边,求其三个角.
(4) 利用余弦定理判断三角形形状:
①勾股定理是余弦定理的特殊情况,.
②在中,,所以为锐角;
若,,同理可得角、为锐角.
当,,都成立时,为锐角三角形.
③在中,若,
所以为钝角,则是钝角三角形.
同理:若,则是钝角三角形且为钝角;
若,则是钝角三角形且为钝角.
要点三、解斜三角形的类型
1.已知两角一边,用正弦定理,有解时,只有一解.
2.已知两边及其一边的对角,用正弦定理,有解的情况可分为以下情况,在中,已知和角时,解的情况如下:
(1)若A为锐角时:
如图:
(2)若A为直角或钝角时:
3.已知三边,用余弦定理有解时,只有一解.
4.已知两边及夹角,用余弦定理,必有一解.
要点四、三角形面积公式
1.(表示边上的高);
2.;
3.;
4.;
要点五、实际问题中的常用角
1. 仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角,如图所示:
2.方位角:一般指正北方向线顺时针到目标方向线的水平角. 方位角的取值范围为0°~360°.
如图,点的方位角是。
3. 坡角和坡度
坡面与地平面所成的角度,叫做坡角;坡面的铅直高度和水平宽度的比叫做坡度或者_??????_,常用字母i表示。坡比是坡角的正切值。
【典型考法1:角度变化】
例1.在△ABC中,若2cos Bsin A=sin C,则△ABC的形状一定是( ).
A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
答案 C
解析 ∵2cos Bsin A=sin C=sin(A+B),
∴sin Acos B-cos Asin B=0,
即sin(A-B)=0,∴A=B.
【变式1】△ABC中,若==,则△ABC的形状是_______.
答案 等边三角形
解析 ∵a=2Rsin A,b=2Rsin B,c=2Rsin C,
∴==,∴sin=sin=sin,
又∵A+B+C=π,∴++=.
∴==,∴A=B=C=.
【变式2】在锐角△ABC中,角A、B、C的对边分别为a、b、c.若+=6cos C,则+的值是______.
解析 由+=6cos C,得b2+a2=6abcos C.
化简整理得2(a2+b2)=3c2,将+切化弦,
得·=·
=·=.
根据正、余定理得=
===4.
【变式3】在△ABC中,若则△ABC的形状是______________.
答案:直角三角形;
【典型考法2:正余弦定理混用】
例2.在△ABC中,内角A、B、C的对边分别为a、b、c,已知b2=ac且cos B=
(1)求+的值;
(2)设·=,求a+c的值
解 (1)由cos B=,得sin B= =.
由b2=ac及正弦定理得sin2B=sin Asin C.
于是+=+ ==
===.
(2)由·=得ca·cos B=,由cos B=,可得ca=2,即b2=2.
由余弦定理b2=a2+c2-2ac·cos B,
得a2+c2=b2+2ac·cos B=5,∴(a+c)2=a2+c2+2ac=5+4=9,∴a+c=3.
【变式1】在△ABC中,若,则的值是_______.
答案:1;
【变式2】 在△ABC中,若,且,边上的高为,求角的大小与边的长
答案:解:
,联合
得,即
当时,
当时,
∴当时,
当时,_._
【变式3】在△ABC中,若则△ABC的形状是什么?
答案:解:
或,得或
所以△ABC是直角三角形.
【变式4】的内角所对的边分别为,已知,
(1)求;
(2)若,的面积为,求。
(答案)(1);
(2)。
(解析)
试题分析:利用三角形内角和定理可知,再利用诱导公式化简,利用降幂公式化简,结合求出;利用(1)中结论,利用勾股定理和面积公式求出,从而求出。
试题解析:(1)由题设及,,故。
上式两边平方,整理得,
解得(舍去),。
(2)由得,故。
又,则。
由余弦定理及得:
所以b=2。
【典型考法3:范围求值】
例3.△ABC的内角A,B,C的对边分别为a,b,c,已知.
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
【答案】(1)B=60°;(2).
【解析】(1)由题设及正弦定理得.
因为sinA0,所以.
由,可得,故.
因为,故,因此B=60°.
(2)由题设及(1)知△ABC的面积.
由正弦定理得.
由于△ABC为锐角三角形,故0°
【变式1】△的内角,,的对边分别为,,,且满足,.
(1)求角的大小;
(2)求△周长的最大值.
解:(Ⅰ)∵,
由正弦定理,
得,
,即,
又∵,
∵,∴.
(Ⅱ)由(Ⅰ)可知
,
∴当时,周长最大
最大值为2+4=6,即周长最大值是6
【变式2】在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)证明:;
(Ⅱ)求的最小值.
【解析】(Ⅰ)由
得,
所以,由正弦定理,得.
(Ⅱ)由
.
所以的最小值为.
【典型考法4:图形分析】
例4.已知△ABC中,AB=BC,AC=2,点D在边AC上,且AD=2CD,
∠ABD=2∠CBD。
(1)求∠ABC的大小;
(2)求△ABC的面积。
【变式1】如图,在中,是边的中点,,.
(Ⅰ)求角的大小;
(Ⅱ)若,求的面积.
【解析】(Ⅰ)由,得,
由,得
又,
所以,
=,
又,所以.
(Ⅱ)解法一:由(Ⅰ)知,
在中,由正弦定理,得,
所以, .
因为是边的中点,所以,.
故 .
解法二:由(Ⅰ)知,在中,
由正弦定理,得,
所以, .
因为是边的中点,所以,
所以, .
【变式2】如图,在中, ,点在边上, , 为垂足.
(1)若的面积为,求的长;
(2)若,求角的大小.
【答案】(1) ;(2) .
【典型考法5:实际应用】
例5.如图所示,某镇有一块空地,其中,,.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖,其中,都在边上,且,挖出的泥土堆放在地带上形成假山,剩下的地带开设儿童游乐场.为安全起见,需在的周围安装防护网.
(1)当时,求防护网的总长度;
(2)为节省投入资金,人工湖的面积要尽可能小,问如何设计施工方案,可使的面积最小?最小面积是多少?
【答案】(1) ;(2)当时,最小值为.
、
【变式1】如图,一山顶有一信号塔(所在的直线与地平面垂直),在山脚处测得塔尖的仰角为,沿倾斜角为的山坡向上前进米后到达处,测得的仰角为.
(1)求的长;
(2)若, , , ,求信号塔的高度.
【答案】(1) ;(2) .
【解析】(1)在中, , , .由正弦定理, ;
(2)由(1)及条件知, , , , .
由正弦定理得
【变式2】如图所示,在海岸A处,发现北偏东45°方向,距A为()km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以km/h的速度追截走私船.此时走私船正以10km/h的速度从B处向北偏东30°方向逃窜,则缉私船沿什么方向能最快追上走私船?并求出所需要的时间.
【解析】设缉私船追上走私船需,则,.
由余弦定理,得
,
由正弦定理,得,
∴,而,
∴
∴,.
∴,即,∴
答:缉私船向东偏北方向,只需便能追上走私船.
.
_21?????????è?????(www.21cnjy.com)_
