沪教版 九下数学 27.1圆的确定 同步学案+练习(Word版 含答案)
文档属性
| 名称 | 沪教版 九下数学 27.1圆的确定 同步学案+练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 271.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 09:49:47 | ||
图片预览




文档简介
27.1
圆的确定
【学习目标】
【1】了解圆的有关概念,理解垂径定理并灵活运用垂径定理及圆的概念解决一些实际问题.
【2】探索并证明垂径定理及利用垂径定理解决一些实际问题.
【主要概念】
【圆】在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.固定的端点O叫做圆心,线段OA叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”
注意:①图上各点到定点(圆心O)的距离都等于定长(半径r);
②到定点的距离等于定长的点都在同一个圆上.
③圆是轴对称图形,它的对称轴是直径,对称轴是任何一条过圆心的直线
【圆的新定义】圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.
①连接圆上任意两点的线段叫做弦,如图线段AC,AB;
②经过圆心的弦叫做直径,如图24-1线段AB;
③圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”,读作“圆弧”或“弧AC”.大于半圆的弧(如图所示叫做优弧,小于半圆的弧(如图所示)或叫做劣弧.
④圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
【垂径定理】平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
【圆与点的关系】设一个圆的半径长为R,点P与圆心O的距离为d,
则(1)点P在圆外
d>R
(2)点P在圆上
d=R
(3)点P在圆内
d【定理】不共线的三点确定一个圆
【经典例题】
【例1】举出生活中的圆三、四个;并说明形成圆的方法有多少种?
【解】如车轮、杯口、时针等;圆规:固定一个定点,固定一个长度,绕定点拉紧运动就形成一个圆.
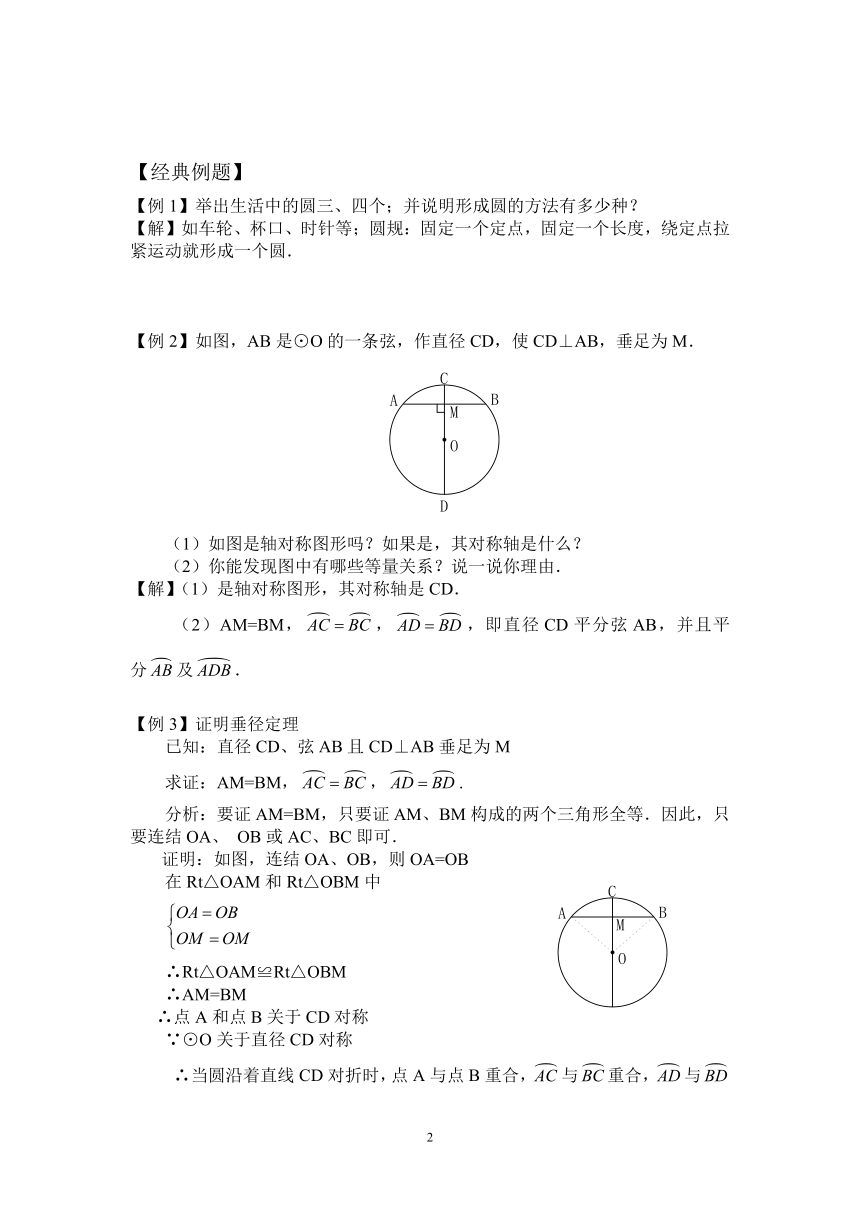
【例2】如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
(1)如图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你理由.
【解】(1)是轴对称图形,其对称轴是CD.
(2)AM=BM,,,即直径CD平分弦AB,并且平
分及.
【例3】证明垂径定理
已知:直径CD、弦AB且CD⊥AB垂足为M
求证:AM=BM,,.
分析:要证AM=BM,只要证AM、BM构成的两个三角形全等.因此,只要连结OA、OB或AC、BC即可.
证明:如图,连结OA、OB,则OA=OB
在Rt△OAM和Rt△OBM中
HYPERLINK
"http://www.czsx.com.cn"
∴Rt△OAM≌Rt△OBM
∴AM=BM
∴点A和点B关于CD对称
∵⊙O关于直径CD对称
∴当圆沿着直线CD对折时,点A与点B重合,与重合,与重合.
∴,
【例4】如图,一条公路的转弯处是一段圆弦(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
【分析】例1是垂径定理的应用,解题过程中使用了列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.
【解】如图,连接OC
设弯路的半径为R,则OF=(R-90)m
∵OE⊥CD
∴CF=CD=×600=300(m)
根据勾股定理,得:OC2=CF2+OF2
即R2=3002+(R-90)2
解得R=545
∴这段弯路的半径为545m.
【例5】有一石拱桥的桥拱是圆弧形,如图24-5所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面宽MN=32m时是否需要采取紧急措施?请说明理由.
【分析】要求当洪水到来时,水面宽MN=32m是否需要采取紧急措施,只要求出DE的长,因此只要求半径R,然后运用几何代数解求R.
【解】不需要采取紧急措施
设OA=R,在Rt△AOC中,AC=30,CD=18
R2=302+(R-18)2
R2=900+R2-36R+324
解得R=34(m)
连接OM,设DE=x,在Rt△MOE中,ME=16
342=162+(34-x)2
162+342-68x+x2=342
x2-68x+256=0
解得x1=4,x2=64(不合设)
∴DE=4
∴不需采取紧急措施.
【例6】已知⊙A的圆心坐标为,半径为5,判断下列各点与⊙A的位置关系。
⑴原点O;⑵B;⑶C
【解】⑴,∴点O在圆上。
⑵,∴点B在圆内
⑶,∴点C在圆外
【例7】已知钝角三角形ABC,用直尺和圆规作出这个三角形的外接圆。
【解】
作法
1、作线段AB的垂直平分线。
2、作线段AC的垂直平分线,设和相交于点O。以点O位圆心,OA为半径作⊙O。⊙O就是所求作的圆。
【例8】如下图,CD所在的直线垂直平分线段AB.怎样使用这样的工具找到圆形工件的圆心?
【解】因为A、B两点在圆上,所以圆心必与A、B两点的距离相等,又因为和一条线段的两个端点距离相等的点在这条线段的垂直平分线上.所以圆心在CD所在的直线上.因此使用这样的工具可以作出圆形工件的任意两条直径.它们的交点就是圆心.
【诊断评价】
一、判断题
1、
钝角三角形的外心在三角形的外部.(
)
2、
锐角三角形的外心在三角形的内部.(
)
二、选择题
1、有一个三角形的外接圆的圆心在它的某一边上则这个三角形一定是
_____________.
A.等边三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
2、
三角形外心具有的性质是
_____________.
A.到三个顶点距离相等
B.到三边距离相等
C.外心必在三角形外
D.到顶点的距离等于它到对边中点的距离的两倍
3、
可以作圆,且只可以作一个圆的条件是
_____________.
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在一直线上的三点
4、下列命题中,正确的命题是
_____________.
A.三点确定一个圆
B.经过四点不能作一个圆
C.三角形有一个且只有一个外接圆
D.三角形外心在三角形的外面
5、两直角边分别为15和20的直角三角形的外接圆半径为
______.
A.12.5
B.25
C.20
D.10
6、
在下列三角形中,外心在它一条边上的三角形是
_____________.
A.三角形的边长分别为2cm,
2cm,
3cm
B.三角形的边长都等于4cm
C.三角形的边长分别为5cm,
12cm,
13cm
D.三角形的边长分别为4cm,
6cm,
8cm
7、下列命题中正确的为__________.
A.三点确定一个圆
B.圆有切只有一个内接三角形
C.三角形的外心是三角形任意两边的垂直平分线的交点
D.面积相等的三角形的外接圆是等圆
8、钝角三角形的外心在__________.
A.三角形的内部
B.三角形的外部
C.三角形的钝角所对的边上
D.以上都有可能
9、己知命题:(1)三角形中最少有一个内角不小于60°;(2)三角形的外心到三角形各边的距离都相等.?
下面判断中正确的是__________.
A.命题(1)(2)都正确
B.命题(1)正确,(2)不正确
C.命题(1)不正确,(2)正确
D.命题(1)(2)都不正确
三、填空题
1.用反证法证明a>b时,应先假设_________.
2.若一个圆经过梯形ABCD的四个顶点,则这个梯形是_________梯形.
四、解答题
1、已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上.
2、如图,在△ABC中,D、E两点分别在AB和AC上,求证CD、BE不可能互相平分.
答案:
一、判断题
1.
√2.
√
二、选择题
1.
B
2.A
3.D
4.C
5.
A
6.
C
7.C
8.B
9.B;
三、填空题
1.a≤b;?
2.等腰;
本周强化练习
一、填空题:
1.锐角三角形的外心在_______.如果一个三角形的外心在它的一边的中点上,
则该三角形是______.如果一个三角形的外心在它的外部,则该三角形是_____.毛
2.边长为6cm的等边三角形的外接圆半径是________.
3.△ABC的三边为2,3,
,设其外心为O,三条高的交点为H,则OH的长为_____.
4.三角形的外心是______的圆心,它是_______的交点,它到_______的距离相等.
5.已知⊙O的直径为2,则⊙O的内接正三角形的边长为_______.
6.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用________
次就可以找到圆形工件的圆心.
二、选择题:
7.下列条件,可以画出圆的是(
)
A.已知圆心
B.已知半径;
C.已知不在同一直线上的三点
D.已知直径
8.三角形的外心是(
)
A.三条中线的交点;
B.三条边的中垂线的交点;
C.三条高的交点;
D.三条角平分线的交点
9.下列命题不正确的是(
)
A.三点确定一个圆
B.三角形的外接圆有且只有一个
C.经过一点有无数个圆
D.经过两点有无数个圆
10.一个三角形的外心在它的内部,则这个三角形一定是(
)
A.等腰三角形
B.直角三角形;
C.锐角三角形
D.等边三角形
11.等腰直角三角形的外接圆半径等于(
)
A.腰长
B.腰长的倍;
C.底边的倍
D.腰上的高
12.平面上不共线的四点,可以确定圆的个数为(
)
A.1个或3个
B.3个或4个
C.1个或3个或4个
D.1个或2个或3个或4个
三、解答题
13.如图,已知:线段AB和一点C(点C不在直线AB上),求作:⊙O,使它经过A、B、C三点。(要求:尺规作图,不写法,保留作图痕迹)
14.如图,A、B、C三点表示三个工厂,要建立一个供水站,
使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
15.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,并说明你给出的等式成立.
16.要将如图所示的破圆轮残片复制完成,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤).
17.已知:AB是⊙O中长为4的弦,P是⊙O上一动点,cos∠APB=,
问是否存在以A、P、B为顶点的面积最大的三角形?若不存在,试说明理由;若存在,求出这个三角形的面积.
18.如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0的两个根(AD答案:
1.三角形内部
直角三角形
钝角三角形
2.2
3.
4.其外接圆
三角形三条边的垂直平分线
三角形三个顶点
5.
6.两
7.C
8.B
9.A
10.C
11.B
12.C
13.略.
14.
略.
15.(1)△FBC是等边三角形,由已知得:
∠BAF=∠MAD=∠DAC=60°=180°-120°=∠BAC,
∴∠BFC=∠BAC=60°,∠BCF=∠BAF=60°,
∴△FBC是等边三角形.
(2)AB=AC+FA.在AB上取一点G,使AG=AC,则由于∠BAC=60°,
故△AGC是等边三角形,
从而∠BGC=∠FAC=120°,
又∠CBG=∠CFA,BC=FC,
故△BCG≌△FCA,
从而BG=FA,又AG=AC,
∴AC+FA=AG+BG=AB.
【探究创新】
16.(1)在残圆上任取三点A、B、C。
(2)分别作弦AB、AC的垂直平分线,
则这两垂直平分线的交点即是所求的圆心
(3)连接OA,则OA的长即是残圆的半径.
17.存在.∵AB不是直径(否则∠APB=90°,而由cos∠APB=
知∠APB<90°,矛盾)
∴取优弧的中点为P点,过P作PD⊥AB于D,
则PD是圆上所有的点中到AB
距离最大的点.
∵AB的长为定值,
∴当P为优弧的中点时,△APB的面积最大,连接PA、PB,
则等腰三角形APB即为所求.
由作法知:圆心O必在PD上,如图所示,连接AO,则由垂径定理得AD=
AB=2.
又∠AOD=∠1+∠2,而∠2=∠3,∠1=∠2
故∠AOD=∠2+∠1=∠2+∠3=∠APB,即cos∠AOD=
,
∴cos∠AOD=,设OD=x,OA=3x,则AD=
,
即=2
,故x=,
∴AO=3x=,OD=x=,
∴PD=OP+OD=
OA+OD=+=2,
∴S△APB=
AB·PD=4.
18.过O作OE⊥AB于E,连接OB,则∠AOE=∠AOB,AE=AB,
∴∠C=∠AOB=∠AOE.
解方程x2-7x+12=0可得DC=4,AD=3,
故AB=,AE=,
可证Rt△ADC∽Rt△AEO,
故,
又AC==5,
AD=3,AE=,
故AO=,
从而S⊙O=.毛
本周强化练习
一、选择题
1.如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是(
).
A.CE=DE
B.
C.∠BAC=∠BAD
D.AC>AD
(1)
(2)
(3)
2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是(
)
A.4
B.6
C.7
D.8
3.如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是(
)
A.AB⊥CD
B.∠AOB=4∠ACD
C.
D.PO=PD
二、填空题
1.如图4,AB为⊙O直径,E是中点,OE交BC于点D,BD=3,AB=10,则AC=_____.
(?http:?/??/?www.czsx.com.cn?)
(4)
(5)
2.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;最长弦长为_______.
3.如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,那么_______(只需写一个正确的结论)
三、综合提高题
1.如图24-11,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM⊥CD,分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.
2.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
(?http:?/??/?www.czsx.com.cn?)
3.(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.
答案:
一、1.D
2.D
3.D
二、1.8
2.8
10
3.AB=CD
三、1.AN=BM
理由:过点O作OE⊥CD于点E,则CE=DE,且CN∥OE∥DM.
∴ON=OM,∴OA-ON=OB-OM,
∴AN=BM.
2.过O作OF⊥CD于F,如右图所示
∵AE=2,EB=6,∴OE=2,
∴EF=,OF=1,连结OD,
在Rt△ODF中,42=12+DF2,DF=,∴CD=2.
3.(1)AC、AD在AB的同旁,如右图所示:
∵AB=16,AC=8,AD=8,
∴AC=(AB),∴∠CAB=60°,
同理可得∠DAB=30°,
∴∠DAC=30°.
(2)AC、AD在AB的异旁,同理可得:∠DAC=60°+30°=90°.
_
B
_
A
_
C
_
O
_
D
PAGE
21
圆的确定
【学习目标】
【1】了解圆的有关概念,理解垂径定理并灵活运用垂径定理及圆的概念解决一些实际问题.
【2】探索并证明垂径定理及利用垂径定理解决一些实际问题.
【主要概念】
【圆】在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.固定的端点O叫做圆心,线段OA叫做半径.
以点O为圆心的圆,记作“⊙O”,读作“圆O”
注意:①图上各点到定点(圆心O)的距离都等于定长(半径r);
②到定点的距离等于定长的点都在同一个圆上.
③圆是轴对称图形,它的对称轴是直径,对称轴是任何一条过圆心的直线
【圆的新定义】圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.
①连接圆上任意两点的线段叫做弦,如图线段AC,AB;
②经过圆心的弦叫做直径,如图24-1线段AB;
③圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”,读作“圆弧”或“弧AC”.大于半圆的弧(如图所示叫做优弧,小于半圆的弧(如图所示)或叫做劣弧.
④圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
【垂径定理】平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
【圆与点的关系】设一个圆的半径长为R,点P与圆心O的距离为d,
则(1)点P在圆外
d>R
(2)点P在圆上
d=R
(3)点P在圆内
d
【经典例题】
【例1】举出生活中的圆三、四个;并说明形成圆的方法有多少种?
【解】如车轮、杯口、时针等;圆规:固定一个定点,固定一个长度,绕定点拉紧运动就形成一个圆.
【例2】如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
(1)如图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你理由.
【解】(1)是轴对称图形,其对称轴是CD.
(2)AM=BM,,,即直径CD平分弦AB,并且平
分及.
【例3】证明垂径定理
已知:直径CD、弦AB且CD⊥AB垂足为M
求证:AM=BM,,.
分析:要证AM=BM,只要证AM、BM构成的两个三角形全等.因此,只要连结OA、OB或AC、BC即可.
证明:如图,连结OA、OB,则OA=OB
在Rt△OAM和Rt△OBM中
HYPERLINK
"http://www.czsx.com.cn"
∴Rt△OAM≌Rt△OBM
∴AM=BM
∴点A和点B关于CD对称
∵⊙O关于直径CD对称
∴当圆沿着直线CD对折时,点A与点B重合,与重合,与重合.
∴,
【例4】如图,一条公路的转弯处是一段圆弦(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
【分析】例1是垂径定理的应用,解题过程中使用了列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.
【解】如图,连接OC
设弯路的半径为R,则OF=(R-90)m
∵OE⊥CD
∴CF=CD=×600=300(m)
根据勾股定理,得:OC2=CF2+OF2
即R2=3002+(R-90)2
解得R=545
∴这段弯路的半径为545m.
【例5】有一石拱桥的桥拱是圆弧形,如图24-5所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面宽MN=32m时是否需要采取紧急措施?请说明理由.
【分析】要求当洪水到来时,水面宽MN=32m是否需要采取紧急措施,只要求出DE的长,因此只要求半径R,然后运用几何代数解求R.
【解】不需要采取紧急措施
设OA=R,在Rt△AOC中,AC=30,CD=18
R2=302+(R-18)2
R2=900+R2-36R+324
解得R=34(m)
连接OM,设DE=x,在Rt△MOE中,ME=16
342=162+(34-x)2
162+342-68x+x2=342
x2-68x+256=0
解得x1=4,x2=64(不合设)
∴DE=4
∴不需采取紧急措施.
【例6】已知⊙A的圆心坐标为,半径为5,判断下列各点与⊙A的位置关系。
⑴原点O;⑵B;⑶C
【解】⑴,∴点O在圆上。
⑵,∴点B在圆内
⑶,∴点C在圆外
【例7】已知钝角三角形ABC,用直尺和圆规作出这个三角形的外接圆。
【解】
作法
1、作线段AB的垂直平分线。
2、作线段AC的垂直平分线,设和相交于点O。以点O位圆心,OA为半径作⊙O。⊙O就是所求作的圆。
【例8】如下图,CD所在的直线垂直平分线段AB.怎样使用这样的工具找到圆形工件的圆心?
【解】因为A、B两点在圆上,所以圆心必与A、B两点的距离相等,又因为和一条线段的两个端点距离相等的点在这条线段的垂直平分线上.所以圆心在CD所在的直线上.因此使用这样的工具可以作出圆形工件的任意两条直径.它们的交点就是圆心.
【诊断评价】
一、判断题
1、
钝角三角形的外心在三角形的外部.(
)
2、
锐角三角形的外心在三角形的内部.(
)
二、选择题
1、有一个三角形的外接圆的圆心在它的某一边上则这个三角形一定是
_____________.
A.等边三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
2、
三角形外心具有的性质是
_____________.
A.到三个顶点距离相等
B.到三边距离相等
C.外心必在三角形外
D.到顶点的距离等于它到对边中点的距离的两倍
3、
可以作圆,且只可以作一个圆的条件是
_____________.
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在一直线上的三点
4、下列命题中,正确的命题是
_____________.
A.三点确定一个圆
B.经过四点不能作一个圆
C.三角形有一个且只有一个外接圆
D.三角形外心在三角形的外面
5、两直角边分别为15和20的直角三角形的外接圆半径为
______.
A.12.5
B.25
C.20
D.10
6、
在下列三角形中,外心在它一条边上的三角形是
_____________.
A.三角形的边长分别为2cm,
2cm,
3cm
B.三角形的边长都等于4cm
C.三角形的边长分别为5cm,
12cm,
13cm
D.三角形的边长分别为4cm,
6cm,
8cm
7、下列命题中正确的为__________.
A.三点确定一个圆
B.圆有切只有一个内接三角形
C.三角形的外心是三角形任意两边的垂直平分线的交点
D.面积相等的三角形的外接圆是等圆
8、钝角三角形的外心在__________.
A.三角形的内部
B.三角形的外部
C.三角形的钝角所对的边上
D.以上都有可能
9、己知命题:(1)三角形中最少有一个内角不小于60°;(2)三角形的外心到三角形各边的距离都相等.?
下面判断中正确的是__________.
A.命题(1)(2)都正确
B.命题(1)正确,(2)不正确
C.命题(1)不正确,(2)正确
D.命题(1)(2)都不正确
三、填空题
1.用反证法证明a>b时,应先假设_________.
2.若一个圆经过梯形ABCD的四个顶点,则这个梯形是_________梯形.
四、解答题
1、已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上.
2、如图,在△ABC中,D、E两点分别在AB和AC上,求证CD、BE不可能互相平分.
答案:
一、判断题
1.
√2.
√
二、选择题
1.
B
2.A
3.D
4.C
5.
A
6.
C
7.C
8.B
9.B;
三、填空题
1.a≤b;?
2.等腰;
本周强化练习
一、填空题:
1.锐角三角形的外心在_______.如果一个三角形的外心在它的一边的中点上,
则该三角形是______.如果一个三角形的外心在它的外部,则该三角形是_____.毛
2.边长为6cm的等边三角形的外接圆半径是________.
3.△ABC的三边为2,3,
,设其外心为O,三条高的交点为H,则OH的长为_____.
4.三角形的外心是______的圆心,它是_______的交点,它到_______的距离相等.
5.已知⊙O的直径为2,则⊙O的内接正三角形的边长为_______.
6.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用________
次就可以找到圆形工件的圆心.
二、选择题:
7.下列条件,可以画出圆的是(
)
A.已知圆心
B.已知半径;
C.已知不在同一直线上的三点
D.已知直径
8.三角形的外心是(
)
A.三条中线的交点;
B.三条边的中垂线的交点;
C.三条高的交点;
D.三条角平分线的交点
9.下列命题不正确的是(
)
A.三点确定一个圆
B.三角形的外接圆有且只有一个
C.经过一点有无数个圆
D.经过两点有无数个圆
10.一个三角形的外心在它的内部,则这个三角形一定是(
)
A.等腰三角形
B.直角三角形;
C.锐角三角形
D.等边三角形
11.等腰直角三角形的外接圆半径等于(
)
A.腰长
B.腰长的倍;
C.底边的倍
D.腰上的高
12.平面上不共线的四点,可以确定圆的个数为(
)
A.1个或3个
B.3个或4个
C.1个或3个或4个
D.1个或2个或3个或4个
三、解答题
13.如图,已知:线段AB和一点C(点C不在直线AB上),求作:⊙O,使它经过A、B、C三点。(要求:尺规作图,不写法,保留作图痕迹)
14.如图,A、B、C三点表示三个工厂,要建立一个供水站,
使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
15.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,并说明你给出的等式成立.
16.要将如图所示的破圆轮残片复制完成,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤).
17.已知:AB是⊙O中长为4的弦,P是⊙O上一动点,cos∠APB=,
问是否存在以A、P、B为顶点的面积最大的三角形?若不存在,试说明理由;若存在,求出这个三角形的面积.
18.如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0的两个根(AD
1.三角形内部
直角三角形
钝角三角形
2.2
3.
4.其外接圆
三角形三条边的垂直平分线
三角形三个顶点
5.
6.两
7.C
8.B
9.A
10.C
11.B
12.C
13.略.
14.
略.
15.(1)△FBC是等边三角形,由已知得:
∠BAF=∠MAD=∠DAC=60°=180°-120°=∠BAC,
∴∠BFC=∠BAC=60°,∠BCF=∠BAF=60°,
∴△FBC是等边三角形.
(2)AB=AC+FA.在AB上取一点G,使AG=AC,则由于∠BAC=60°,
故△AGC是等边三角形,
从而∠BGC=∠FAC=120°,
又∠CBG=∠CFA,BC=FC,
故△BCG≌△FCA,
从而BG=FA,又AG=AC,
∴AC+FA=AG+BG=AB.
【探究创新】
16.(1)在残圆上任取三点A、B、C。
(2)分别作弦AB、AC的垂直平分线,
则这两垂直平分线的交点即是所求的圆心
(3)连接OA,则OA的长即是残圆的半径.
17.存在.∵AB不是直径(否则∠APB=90°,而由cos∠APB=
知∠APB<90°,矛盾)
∴取优弧的中点为P点,过P作PD⊥AB于D,
则PD是圆上所有的点中到AB
距离最大的点.
∵AB的长为定值,
∴当P为优弧的中点时,△APB的面积最大,连接PA、PB,
则等腰三角形APB即为所求.
由作法知:圆心O必在PD上,如图所示,连接AO,则由垂径定理得AD=
AB=2.
又∠AOD=∠1+∠2,而∠2=∠3,∠1=∠2
故∠AOD=∠2+∠1=∠2+∠3=∠APB,即cos∠AOD=
,
∴cos∠AOD=,设OD=x,OA=3x,则AD=
,
即=2
,故x=,
∴AO=3x=,OD=x=,
∴PD=OP+OD=
OA+OD=+=2,
∴S△APB=
AB·PD=4.
18.过O作OE⊥AB于E,连接OB,则∠AOE=∠AOB,AE=AB,
∴∠C=∠AOB=∠AOE.
解方程x2-7x+12=0可得DC=4,AD=3,
故AB=,AE=,
可证Rt△ADC∽Rt△AEO,
故,
又AC==5,
AD=3,AE=,
故AO=,
从而S⊙O=.毛
本周强化练习
一、选择题
1.如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是(
).
A.CE=DE
B.
C.∠BAC=∠BAD
D.AC>AD
(1)
(2)
(3)
2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是(
)
A.4
B.6
C.7
D.8
3.如图3,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是(
)
A.AB⊥CD
B.∠AOB=4∠ACD
C.
D.PO=PD
二、填空题
1.如图4,AB为⊙O直径,E是中点,OE交BC于点D,BD=3,AB=10,则AC=_____.
(?http:?/??/?www.czsx.com.cn?)
(4)
(5)
2.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;最长弦长为_______.
3.如图5,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,那么_______(只需写一个正确的结论)
三、综合提高题
1.如图24-11,AB为⊙O的直径,CD为弦,过C、D分别作CN⊥CD、DM⊥CD,分别交AB于N、M,请问图中的AN与BM是否相等,说明理由.
2.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
(?http:?/??/?www.czsx.com.cn?)
3.(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.
答案:
一、1.D
2.D
3.D
二、1.8
2.8
10
3.AB=CD
三、1.AN=BM
理由:过点O作OE⊥CD于点E,则CE=DE,且CN∥OE∥DM.
∴ON=OM,∴OA-ON=OB-OM,
∴AN=BM.
2.过O作OF⊥CD于F,如右图所示
∵AE=2,EB=6,∴OE=2,
∴EF=,OF=1,连结OD,
在Rt△ODF中,42=12+DF2,DF=,∴CD=2.
3.(1)AC、AD在AB的同旁,如右图所示:
∵AB=16,AC=8,AD=8,
∴AC=(AB),∴∠CAB=60°,
同理可得∠DAB=30°,
∴∠DAC=30°.
(2)AC、AD在AB的异旁,同理可得:∠DAC=60°+30°=90°.
_
B
_
A
_
C
_
O
_
D
PAGE
21
