北师大版2020年数学九年级上册4.6 利用相似三角形测高课件(共20张PPT)
文档属性
| 名称 | 北师大版2020年数学九年级上册4.6 利用相似三角形测高课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 23:13:41 | ||
图片预览








文档简介
(共20张PPT)
北师大版数学九年级上册
第四章
图形的相似
4.6
利用相似三角形测高
1.学生通过探索实际问题来体验测量中对相似三角形有关知识的应用。
2.经历应用相似三角形的有关知识去解决简单的实际问题的全过程。
3.全力培养学生的应用意识,和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力。
学习目标
想一想
怎样测量旗杆的高度,有几种方法?
导入新知
知识模块一 探索利用相似三角形测高的方法
(一)自主探究
学校操场上的国旗旗杆的高度是多少?
你有什么办法测量?
探究新知
测量旗杆高度的常见方法有:
(1)利用“同一时刻的物高与_________成比例”构造相似三角形;
(2)利用“视线、标杆和物高”构造___________;
(3)利用“平面镜中入射角与_______相等”构造相似三角形.
影长
相似三角形
反射角
(二)合作探究
1.利用阳光下的影子来测量旗杆的高度,如图1:
操作方法:一名学生在直立于旗杆影子的顶端处如图2,测出该同学的影长和此时旗杆的影长.
图1
点拨∵太阳的光线是平行的,
∴AE∥CB,∴∠AEB=∠CBD,
∵人与旗杆是垂直于地面的,
∴∠ABE=∠CDB,∴△ABE∽△CDB,
图2
代入测量数据即可求出旗杆CD的高度.
2.利用镜子的反射
操作方法:如图3,选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.
图3
点拨:∵入射角=反射角,
∴∠AEB=∠CED.
∵人、旗杆都垂直于地面,
∴∠B=∠D=90°,∴△AEB∽△CED,
因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度.
知识模块二 利用相似三角形测高的应用
(一)自主探究
1.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m
B.7m
C.8.5m D.9m
D
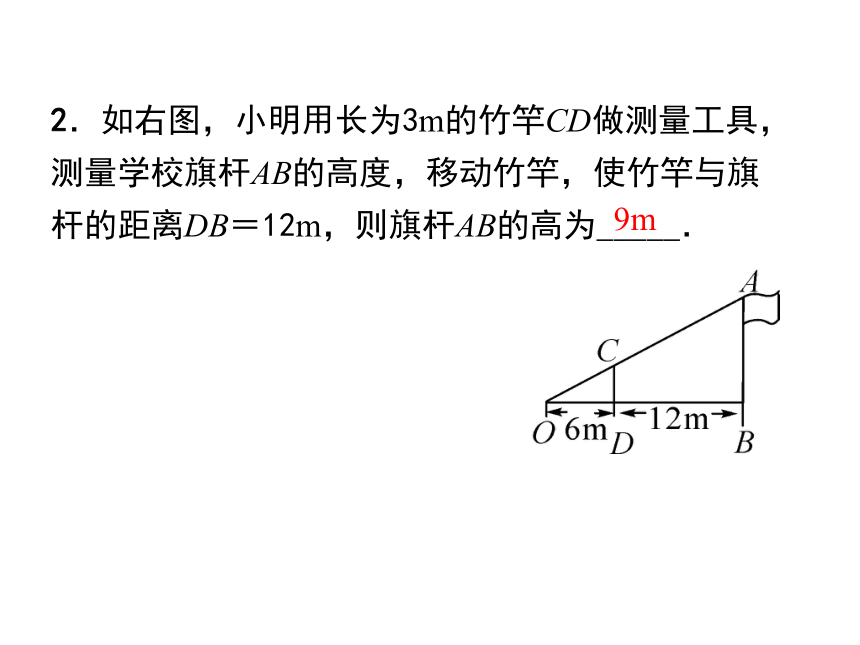
2.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为_____.
9m
(二)合作探究
例
如图,一人拿着一支刻有厘米分画的小尺,站
在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.
分析:本题所叙述的内容可以画出如上图那样的几何图形,即DF=60厘米=0.6米,
GF=12厘米=0.12米,CE=30米,求BC.由于△ADF∽△AEC,
又△AGF∽△ABC,
从而可以求出BC的长.
解:∵AE⊥EC,DF∥EC,
∴∠ADF=∠AEC,∠DAF=∠EAC,
∴△ADF∽△AEC.
又GF⊥EC,BC⊥EC,
∴GF∥BC,∠AFG=∠ACB,∠AGF=∠ABC,∴△AGF∽△ABC,
又DF=60厘米=0.6米,GF=12厘米=0.12米,EC=30米,∴BC=6米.即电线杆的高为6米.
练习
1.高4m的旗杆在水平地面上的影子长6m,此时
测得附近一个建筑物的影子长24m,求该建筑物的高度
解:设建筑物高度为x米,
得:x=16,答:建筑物高度为16米.
1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )
A.仰角
B.树的影长
C.标杆的影长
D.都不需要
B
课堂练习
2.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是(
)
A.6m B.8m C.18m D.21m
B
3.如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将(
)
A.变大
B.变小
C.不变
D.无法判断
C
4.小华做小孔成像实验(如图所示),已知蜡烛与成像板之间的距离为15cm,则蜡烛与成像板之间的小孔纸板应放在离蜡烛______cm的地方时,蜡烛焰AB是像
的一半。
5
5.如图,铁道口的栏杆短臂长1米,长臂长16米,当短臂的端点下降0.5米时,长臂端点应升高_____.
8
6.小明想知道学校旗杆的高,在他与旗杆之间的地面上直立一根2米的标竿EF,小明适当调整自己的位置使得旗杆的顶端C、标竿的顶端F与眼睛D恰好在一条直线上,量得小明高AD为1.6米,小明脚到标杆底端的距离AE为0.5米,小明脚到旗杆底端的距离AB为8米.请你根据数据求旗杆BC的高度.
解:证△DCG∽△DFH,
求得CG=6.4米,BC=8米.
一
、相似三角形的应用主要有如下两个方面
1.测高(不能直接使用皮尺或刻度尺量的)
2.测距
、测高的方法
解决实际问题时(如测高、测距),
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
一般有以下步骤:①审题
②构建图形
③利用相似解决问题
总结新知
再
见
北师大版数学九年级上册
第四章
图形的相似
4.6
利用相似三角形测高
1.学生通过探索实际问题来体验测量中对相似三角形有关知识的应用。
2.经历应用相似三角形的有关知识去解决简单的实际问题的全过程。
3.全力培养学生的应用意识,和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力。
学习目标
想一想
怎样测量旗杆的高度,有几种方法?
导入新知
知识模块一 探索利用相似三角形测高的方法
(一)自主探究
学校操场上的国旗旗杆的高度是多少?
你有什么办法测量?
探究新知
测量旗杆高度的常见方法有:
(1)利用“同一时刻的物高与_________成比例”构造相似三角形;
(2)利用“视线、标杆和物高”构造___________;
(3)利用“平面镜中入射角与_______相等”构造相似三角形.
影长
相似三角形
反射角
(二)合作探究
1.利用阳光下的影子来测量旗杆的高度,如图1:
操作方法:一名学生在直立于旗杆影子的顶端处如图2,测出该同学的影长和此时旗杆的影长.
图1
点拨∵太阳的光线是平行的,
∴AE∥CB,∴∠AEB=∠CBD,
∵人与旗杆是垂直于地面的,
∴∠ABE=∠CDB,∴△ABE∽△CDB,
图2
代入测量数据即可求出旗杆CD的高度.
2.利用镜子的反射
操作方法:如图3,选一名学生作为观测者.在他与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端.测出此时他的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度.
图3
点拨:∵入射角=反射角,
∴∠AEB=∠CED.
∵人、旗杆都垂直于地面,
∴∠B=∠D=90°,∴△AEB∽△CED,
因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度.
知识模块二 利用相似三角形测高的应用
(一)自主探究
1.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m
B.7m
C.8.5m D.9m
D
2.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为_____.
9m
(二)合作探究
例
如图,一人拿着一支刻有厘米分画的小尺,站
在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.
分析:本题所叙述的内容可以画出如上图那样的几何图形,即DF=60厘米=0.6米,
GF=12厘米=0.12米,CE=30米,求BC.由于△ADF∽△AEC,
又△AGF∽△ABC,
从而可以求出BC的长.
解:∵AE⊥EC,DF∥EC,
∴∠ADF=∠AEC,∠DAF=∠EAC,
∴△ADF∽△AEC.
又GF⊥EC,BC⊥EC,
∴GF∥BC,∠AFG=∠ACB,∠AGF=∠ABC,∴△AGF∽△ABC,
又DF=60厘米=0.6米,GF=12厘米=0.12米,EC=30米,∴BC=6米.即电线杆的高为6米.
练习
1.高4m的旗杆在水平地面上的影子长6m,此时
测得附近一个建筑物的影子长24m,求该建筑物的高度
解:设建筑物高度为x米,
得:x=16,答:建筑物高度为16米.
1.要测量出一棵树的高度,除了测量出人高与人的影长外,还需要测出( )
A.仰角
B.树的影长
C.标杆的影长
D.都不需要
B
课堂练习
2.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是(
)
A.6m B.8m C.18m D.21m
B
3.如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将(
)
A.变大
B.变小
C.不变
D.无法判断
C
4.小华做小孔成像实验(如图所示),已知蜡烛与成像板之间的距离为15cm,则蜡烛与成像板之间的小孔纸板应放在离蜡烛______cm的地方时,蜡烛焰AB是像
的一半。
5
5.如图,铁道口的栏杆短臂长1米,长臂长16米,当短臂的端点下降0.5米时,长臂端点应升高_____.
8
6.小明想知道学校旗杆的高,在他与旗杆之间的地面上直立一根2米的标竿EF,小明适当调整自己的位置使得旗杆的顶端C、标竿的顶端F与眼睛D恰好在一条直线上,量得小明高AD为1.6米,小明脚到标杆底端的距离AE为0.5米,小明脚到旗杆底端的距离AB为8米.请你根据数据求旗杆BC的高度.
解:证△DCG∽△DFH,
求得CG=6.4米,BC=8米.
一
、相似三角形的应用主要有如下两个方面
1.测高(不能直接使用皮尺或刻度尺量的)
2.测距
、测高的方法
解决实际问题时(如测高、测距),
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决
一般有以下步骤:①审题
②构建图形
③利用相似解决问题
总结新知
再
见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
