初中数学湘教版八年级上册2.4线段的垂直平分线同步练习(word版含解析)
文档属性
| 名称 | 初中数学湘教版八年级上册2.4线段的垂直平分线同步练习(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 104.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 16:23:12 | ||
图片预览



文档简介
初中数学湘教版八年级上册第二章2.4线段的垂直平分线同步练习
一、选择题
如图,在中,,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分,,则BD的长为
A.
B.
C.
D.
如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB、AC、BC,形成一个三角形.若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在
A.
三条中线的交点处
B.
三条高所在直线的交点处
C.
三条角平分线的交点处
D.
三边的垂直平分线的交点处
如图,中,,AB的垂直平分线交AB于D,交AC于E,且BE平分,求的度数为
A.
B.
C.
D.
已知:如图,在中,,AB的垂直平分线DE,分别交AB,AC于点D,若,,则的周长为
A.
8
B.
10
C.
ll
D.
13
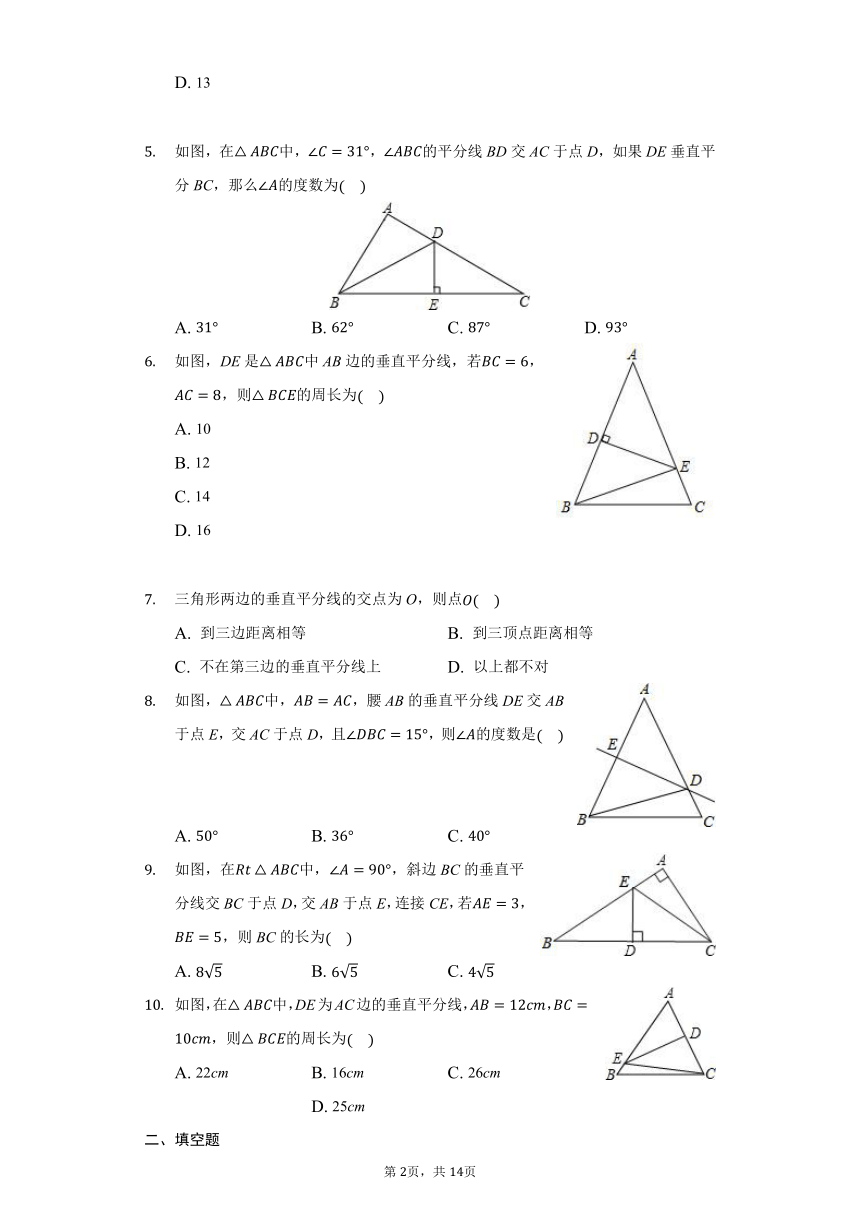
如图,在中,,的平分线BD交AC于点D,如果DE垂直平分BC,那么的度数为
A.
B.
C.
D.
如图,DE是中AB边的垂直平分线,若,,则的周长为
A.
10
B.
12
C.
14
D.
16
三角形两边的垂直平分线的交点为O,则点
A.
到三边距离相等
B.
到三顶点距离相等
C.
不在第三边的垂直平分线上
D.
以上都不对
如图,中,,腰AB的垂直平分线DE交AB于点E,交AC于点D,且,则的度数是
A.
B.
C.
D.
如图,在中,,斜边BC的垂直平分线交BC于点D,交AB于点E,连接CE,若,,则BC的长为
A.
B.
C.
D.
如图,在中,DE为AC边的垂直平分线,,,则的周长为
A.
22cm
B.
16cm
C.
26cm
D.
25cm
二、填空题
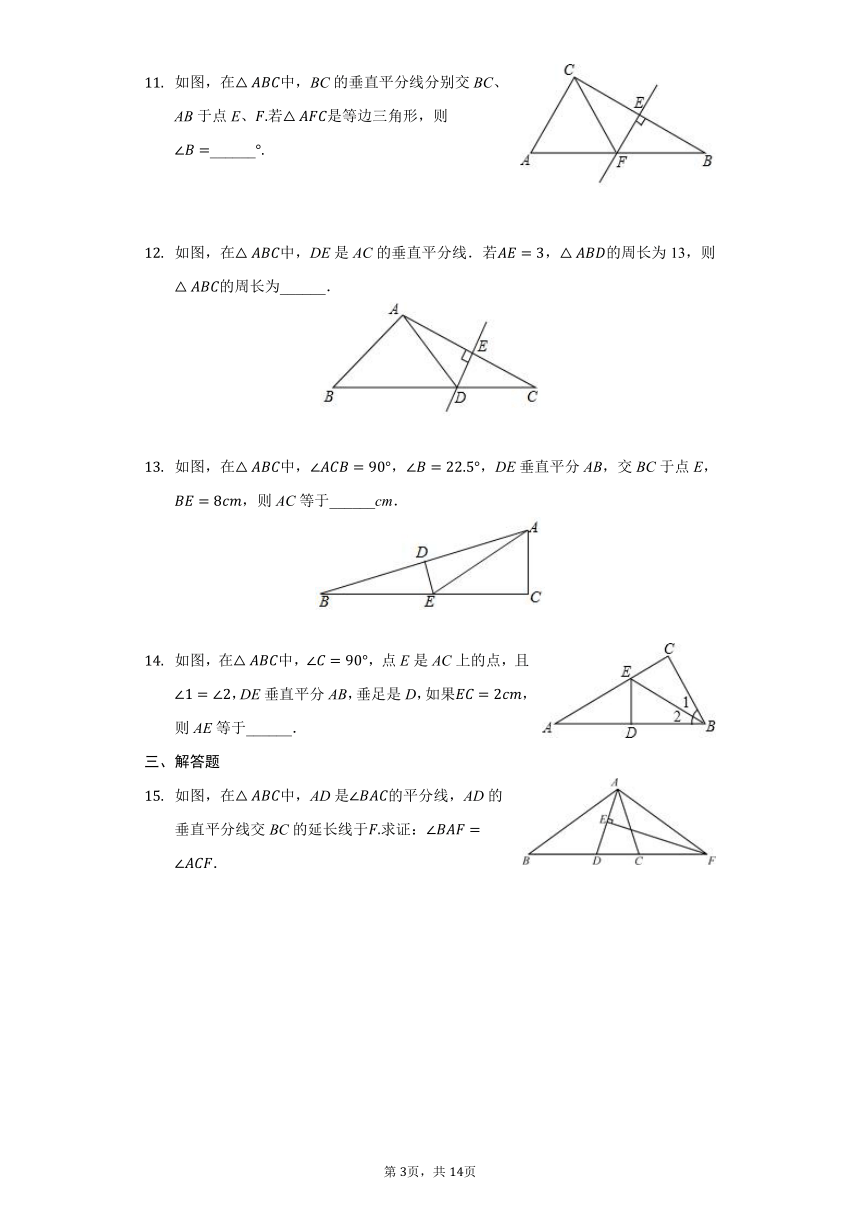
如图,在中,BC的垂直平分线分别交BC、AB于点E、若是等边三角形,则______
如图,在中,DE是AC的垂直平分线.若,的周长为13,则的周长为______.
如图,在中,,,DE垂直平分AB,交BC于点E,,则AC等于______cm.
如图,在中,,点E是AC上的点,且,DE垂直平分AB,垂足是D,如果,则AE等于______.
三、解答题
如图,在中,AD是的平分线,AD的垂直平分线交BC的延长线于求证:.
如图,在中,.
用尺规作图法在AB上找一点P,使得保留作图痕迹,不用写作法
在的条件下,连接PC,若,,求的周长.
如图所示,在等边三角形ABC中,、的平分线交于点O,OB和OC的垂直平分线交BC于E、F,求证:.
已知:在四边形ABCD中,AC,BD相交于点E,且点E是AC的中点,,过点B作,垂足为点F,BF与AC交于点G.
如图1,求证:;
如图2,若;
求证:;
若,的面积为4,求四边形ABCD的面积.
答案和解析
1.【答案】A
【解析】
【分析】
此题综合运用了线段垂直平分线的性质、等腰三角形的性质及判定、直角三角形的性质.
根据CE垂直平分AD,得,再根据等腰三角形的三线合一,得,结合角平分线定义和,得,则,进而求得,则.
【解答】
解:因为CE垂直平分AD,
所以,
所以,
因为CD平分,
所以,
因为,
所以,
所以,
所以,
所以.
所以.
故选A.
2.【答案】D
【解析】解:到A、B、C三地的距离相等,
中转仓的位置应选在三边的垂直平分线的交点处,
故选:D.
根据题意和线段垂直平分线的性质,可以解答本题.
本题考查线段的垂直平分线,解答本题的关键是明确题意,利用线段垂直平分线的性质解答.
3.【答案】D
【解析】解:,
,
的垂直平分线交AB边于点D,交AC边于点E,
,
,
平分,
,
由三角形内角和定理可得:,
解得:,
故选:D.
根据等腰三角形的性质得到,根据线段垂直平分线的性质得到,得到,根据三角形内角和定理计算即可.
本题考查的是线段垂直平分线的性质以及等腰三角形的性质,掌握线段垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
4.【答案】C
【解析】解:的垂直平分线DE分别交AB、AC于点D、E,
,
,
,
,
,
的周长;
故选:C.
由AB的垂直平分线DE分别交AB、AC于点D、E,易得的周长;
此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
5.【答案】C
【解析】解:垂直平分BC,
,
,
平分,
,
,
故选:C.
根据线段垂直平分线的性质得到,根据等腰三角形的性质得到,根据角平分线的定义、三角形内角和定理计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等.
6.【答案】C
【解析】解:是中AB边的垂直平分线,
,
又,,
的周长
,
故选:C.
依据DE是中AB边的垂直平分线,即可得到,再根据,,即可得到的周长.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
7.【答案】B
【解析】解:如图:
连接OA、OB、OC,
为两边BC、AC的垂直平分线的交点,
,,
,
也在AB的垂直平分线上,且O到三顶点的距离相等,
三角形的三角的平分线的交点到三角形的三边距离相等,
即选项A、C、D错误,只有选项B正确;
故选:B.
画出图形,根据线段垂直平分线性质求出,即可得出选项.
本题考查了线段垂直平分线性质的应用,能运用线段垂直平分线性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.
8.【答案】A
【解析】解:的垂直平分线DE交AC于D,
,
,
,
,
,
,
在中,,
,
解得.
故选:A.
根据线段垂直平分线上的点到线段两端点的距离相等可得,再根据等边对等角可得,,然后根据三角形的内角和等于方程求解即可.
本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,熟记性质与定理并列出方程是解题的关键.
9.【答案】C
【解析】解:是BC的垂直平分线,
,
,
,
故选:C.
根据线段垂直平分线的性质得到,根据勾股定理计算即可.
本题考查的是线段垂直平分线线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
10.【答案】A
【解析】解:为AC边的垂直平分线
,
,,
的周长为.
故选:A.
要求的周长,知道,只要求得即可,根据线段垂直平分线的性质得,于是,答案可得.
此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.对线段进行等效转移时解答本题的关键.
11.【答案】30
【解析】解:垂直平分BC,
,
,
为等边三角形,
,
.
故答案为:30.
根据垂直平分线的性质得到,再利用等边三角形的性质得到,从而可得.
本题考查了垂直平分线的性质,等边三角形的性质,外角的性质,解题的关键是利用垂直平分线的性质得到.
12.【答案】19
【解析】解:是AC的垂直平分线,,
,,
,
的周长.
故答案为:19.
由线段的垂直平分线的性质可得,,从而可得答案.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线的性质是解题的关键.
13.【答案】
【解析】解:垂直平分AB,
,
,
,
,
由勾股定理得,,即,
解得,,
故答案为:.
根据线段垂直平分线的性质得到,根据等腰直角三角形的性质、勾股定理计算,得到答案.
本题考查的是线段的垂直平分线的性质、等腰直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
14.【答案】4cm
【解析】解:是线段AB的垂直平分线,
,
,
,
,
,
,
在中,,
,
,
故答案为:4cm.
根据线段垂直平分线的性质得到,根据等腰三角形的性质得到,根据直角三角形的性质得到,根据含的直角三角形的性质解答即可.
本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
15.【答案】证明:是的平分线,
.
是AD的垂直平分线,
.
.
,
,
.
【解析】此题利用了角平分线的定义、线段的垂直平分线性质、等腰三角形的性质等知识由AD是的平分线可以得到,由FE是AD的垂直平分线得到,再根据等边对等角得到,而,,就可以证明题目结论.
16.【答案】解:如图所示,点P即为所求;
由可得,
又,,
的周长.
【解析】作线段BC的垂直平分线交AB于点P,点P即为所求;
由作图可知:,可证的周长.
本题主要考查了复杂作图以及线段垂直平分线的性质,线段垂直平分线上任意一点,到线段两端点的距离相等.
17.【答案】证明:在等边三角形ABC中.
、的平分线交于点O,OB和OC的垂直平分线交BC于E、F,
,,.
,???????????????????????????????????
.
.
【解析】先根据线段的垂直平分线的性质和角平分线性质得到有关的角和线段之间的等量关系:,,;再利用三角形的外角等于不相邻的两内角和求出,从而判定是等边三角形即,通过线段的等量代换求证即可.
此题考查了线段的垂直平分线的性质等和三角形的外角等于不相邻的两内角和以及等边三角形的性质;进行线段的等量代换是正确解答本题的关键.
18.【答案】证明:点E是AC的中点,,
,是等腰三角形,
,
,,
,
,
,
,
,
;
证明:点E是AC的中点,,
是等腰三角形,
,
,
,
在和中,,
≌,
;
解:,点E是AC的中点,
,
,
,
,
,
.
【解析】由线段垂直平分线的性质得,由等腰三角形的性质得,证,则,由和的内角和即可得出结论;
易证是等腰三角形,,得,由ASA证得≌,即可得出结论;
由直角三角形的中线性质得,由求出,则,由,即可得出结果.
本题是三角形综合题,考查了全等三角形的判定与性质、线段垂直平分线的性质、三角形内角和定理、等腰三角形的判定与性质、等腰直角三角形的性质、直角三角形的中线性质、三角形面积的计算等知识;本题综合性强,熟练掌握等腰三角形的性质和全等三角形的判定与性质是解题的关键.
第2页,共14页
第1页,共14页
一、选择题
如图,在中,,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分,,则BD的长为
A.
B.
C.
D.
如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB、AC、BC,形成一个三角形.若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在
A.
三条中线的交点处
B.
三条高所在直线的交点处
C.
三条角平分线的交点处
D.
三边的垂直平分线的交点处
如图,中,,AB的垂直平分线交AB于D,交AC于E,且BE平分,求的度数为
A.
B.
C.
D.
已知:如图,在中,,AB的垂直平分线DE,分别交AB,AC于点D,若,,则的周长为
A.
8
B.
10
C.
ll
D.
13
如图,在中,,的平分线BD交AC于点D,如果DE垂直平分BC,那么的度数为
A.
B.
C.
D.
如图,DE是中AB边的垂直平分线,若,,则的周长为
A.
10
B.
12
C.
14
D.
16
三角形两边的垂直平分线的交点为O,则点
A.
到三边距离相等
B.
到三顶点距离相等
C.
不在第三边的垂直平分线上
D.
以上都不对
如图,中,,腰AB的垂直平分线DE交AB于点E,交AC于点D,且,则的度数是
A.
B.
C.
D.
如图,在中,,斜边BC的垂直平分线交BC于点D,交AB于点E,连接CE,若,,则BC的长为
A.
B.
C.
D.
如图,在中,DE为AC边的垂直平分线,,,则的周长为
A.
22cm
B.
16cm
C.
26cm
D.
25cm
二、填空题
如图,在中,BC的垂直平分线分别交BC、AB于点E、若是等边三角形,则______
如图,在中,DE是AC的垂直平分线.若,的周长为13,则的周长为______.
如图,在中,,,DE垂直平分AB,交BC于点E,,则AC等于______cm.
如图,在中,,点E是AC上的点,且,DE垂直平分AB,垂足是D,如果,则AE等于______.
三、解答题
如图,在中,AD是的平分线,AD的垂直平分线交BC的延长线于求证:.
如图,在中,.
用尺规作图法在AB上找一点P,使得保留作图痕迹,不用写作法
在的条件下,连接PC,若,,求的周长.
如图所示,在等边三角形ABC中,、的平分线交于点O,OB和OC的垂直平分线交BC于E、F,求证:.
已知:在四边形ABCD中,AC,BD相交于点E,且点E是AC的中点,,过点B作,垂足为点F,BF与AC交于点G.
如图1,求证:;
如图2,若;
求证:;
若,的面积为4,求四边形ABCD的面积.
答案和解析
1.【答案】A
【解析】
【分析】
此题综合运用了线段垂直平分线的性质、等腰三角形的性质及判定、直角三角形的性质.
根据CE垂直平分AD,得,再根据等腰三角形的三线合一,得,结合角平分线定义和,得,则,进而求得,则.
【解答】
解:因为CE垂直平分AD,
所以,
所以,
因为CD平分,
所以,
因为,
所以,
所以,
所以,
所以.
所以.
故选A.
2.【答案】D
【解析】解:到A、B、C三地的距离相等,
中转仓的位置应选在三边的垂直平分线的交点处,
故选:D.
根据题意和线段垂直平分线的性质,可以解答本题.
本题考查线段的垂直平分线,解答本题的关键是明确题意,利用线段垂直平分线的性质解答.
3.【答案】D
【解析】解:,
,
的垂直平分线交AB边于点D,交AC边于点E,
,
,
平分,
,
由三角形内角和定理可得:,
解得:,
故选:D.
根据等腰三角形的性质得到,根据线段垂直平分线的性质得到,得到,根据三角形内角和定理计算即可.
本题考查的是线段垂直平分线的性质以及等腰三角形的性质,掌握线段垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
4.【答案】C
【解析】解:的垂直平分线DE分别交AB、AC于点D、E,
,
,
,
,
,
的周长;
故选:C.
由AB的垂直平分线DE分别交AB、AC于点D、E,易得的周长;
此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
5.【答案】C
【解析】解:垂直平分BC,
,
,
平分,
,
,
故选:C.
根据线段垂直平分线的性质得到,根据等腰三角形的性质得到,根据角平分线的定义、三角形内角和定理计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等.
6.【答案】C
【解析】解:是中AB边的垂直平分线,
,
又,,
的周长
,
故选:C.
依据DE是中AB边的垂直平分线,即可得到,再根据,,即可得到的周长.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
7.【答案】B
【解析】解:如图:
连接OA、OB、OC,
为两边BC、AC的垂直平分线的交点,
,,
,
也在AB的垂直平分线上,且O到三顶点的距离相等,
三角形的三角的平分线的交点到三角形的三边距离相等,
即选项A、C、D错误,只有选项B正确;
故选:B.
画出图形,根据线段垂直平分线性质求出,即可得出选项.
本题考查了线段垂直平分线性质的应用,能运用线段垂直平分线性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.
8.【答案】A
【解析】解:的垂直平分线DE交AC于D,
,
,
,
,
,
,
在中,,
,
解得.
故选:A.
根据线段垂直平分线上的点到线段两端点的距离相等可得,再根据等边对等角可得,,然后根据三角形的内角和等于方程求解即可.
本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,熟记性质与定理并列出方程是解题的关键.
9.【答案】C
【解析】解:是BC的垂直平分线,
,
,
,
故选:C.
根据线段垂直平分线的性质得到,根据勾股定理计算即可.
本题考查的是线段垂直平分线线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
10.【答案】A
【解析】解:为AC边的垂直平分线
,
,,
的周长为.
故选:A.
要求的周长,知道,只要求得即可,根据线段垂直平分线的性质得,于是,答案可得.
此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.对线段进行等效转移时解答本题的关键.
11.【答案】30
【解析】解:垂直平分BC,
,
,
为等边三角形,
,
.
故答案为:30.
根据垂直平分线的性质得到,再利用等边三角形的性质得到,从而可得.
本题考查了垂直平分线的性质,等边三角形的性质,外角的性质,解题的关键是利用垂直平分线的性质得到.
12.【答案】19
【解析】解:是AC的垂直平分线,,
,,
,
的周长.
故答案为:19.
由线段的垂直平分线的性质可得,,从而可得答案.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线的性质是解题的关键.
13.【答案】
【解析】解:垂直平分AB,
,
,
,
,
由勾股定理得,,即,
解得,,
故答案为:.
根据线段垂直平分线的性质得到,根据等腰直角三角形的性质、勾股定理计算,得到答案.
本题考查的是线段的垂直平分线的性质、等腰直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
14.【答案】4cm
【解析】解:是线段AB的垂直平分线,
,
,
,
,
,
,
在中,,
,
,
故答案为:4cm.
根据线段垂直平分线的性质得到,根据等腰三角形的性质得到,根据直角三角形的性质得到,根据含的直角三角形的性质解答即可.
本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
15.【答案】证明:是的平分线,
.
是AD的垂直平分线,
.
.
,
,
.
【解析】此题利用了角平分线的定义、线段的垂直平分线性质、等腰三角形的性质等知识由AD是的平分线可以得到,由FE是AD的垂直平分线得到,再根据等边对等角得到,而,,就可以证明题目结论.
16.【答案】解:如图所示,点P即为所求;
由可得,
又,,
的周长.
【解析】作线段BC的垂直平分线交AB于点P,点P即为所求;
由作图可知:,可证的周长.
本题主要考查了复杂作图以及线段垂直平分线的性质,线段垂直平分线上任意一点,到线段两端点的距离相等.
17.【答案】证明:在等边三角形ABC中.
、的平分线交于点O,OB和OC的垂直平分线交BC于E、F,
,,.
,???????????????????????????????????
.
.
【解析】先根据线段的垂直平分线的性质和角平分线性质得到有关的角和线段之间的等量关系:,,;再利用三角形的外角等于不相邻的两内角和求出,从而判定是等边三角形即,通过线段的等量代换求证即可.
此题考查了线段的垂直平分线的性质等和三角形的外角等于不相邻的两内角和以及等边三角形的性质;进行线段的等量代换是正确解答本题的关键.
18.【答案】证明:点E是AC的中点,,
,是等腰三角形,
,
,,
,
,
,
,
,
;
证明:点E是AC的中点,,
是等腰三角形,
,
,
,
在和中,,
≌,
;
解:,点E是AC的中点,
,
,
,
,
,
.
【解析】由线段垂直平分线的性质得,由等腰三角形的性质得,证,则,由和的内角和即可得出结论;
易证是等腰三角形,,得,由ASA证得≌,即可得出结论;
由直角三角形的中线性质得,由求出,则,由,即可得出结果.
本题是三角形综合题,考查了全等三角形的判定与性质、线段垂直平分线的性质、三角形内角和定理、等腰三角形的判定与性质、等腰直角三角形的性质、直角三角形的中线性质、三角形面积的计算等知识;本题综合性强,熟练掌握等腰三角形的性质和全等三角形的判定与性质是解题的关键.
第2页,共14页
第1页,共14页
同课章节目录
