初中数学湘教版八年级上册2.5全等三角形同步练习(word版含答案)
文档属性
| 名称 | 初中数学湘教版八年级上册2.5全等三角形同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 117.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 16:25:02 | ||
图片预览



文档简介
初中数学湘教版八年级上册第二章2.5全等三角形同步练习
一、选择题
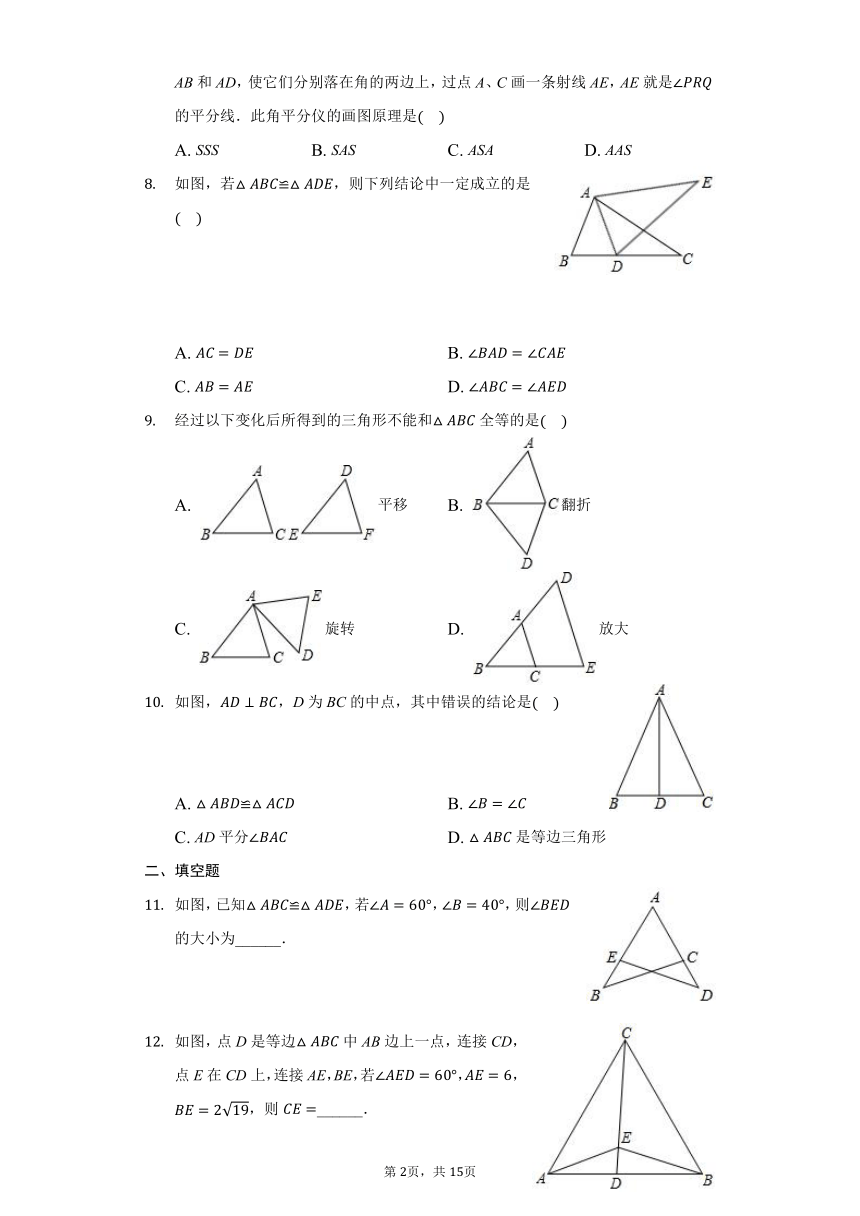
如图,要用“SAS”证≌,若已知,,则还需具备条件
A.
B.
C.
D.
工人师傅常用角尺平分一个任意角做法如下:如图,是一个任意角,在边OA,OB上分别取,移动角尺,使角尺两边相同的刻度分别与M,N重合过角尺顶点C作射线由作法得的依据是
A.
AAS
B.
SAS
C.
ASA
D.
SSS
如果D是中BC边上一点,并且≌,则是
A.
锐角三角形
B.
钝角三角形
C.
直角三角形
D.
等腰三角形
如图,由25个同样大小的小正方形组成的正方形网格中,是格点三角形每个顶点都是格点,在这个正方形网格中画另一个格点三角形,使得它与全等且仅有一条公共边,则符合要求的三角形共能画
A.
5个
B.
6个
C.
7个
D.
8个
花花不慎将一块三角形的玻璃打碎成了如图所示的四块图中所标、、、,若要配块与原来大小一样的三角形玻璃,应该带
A.
第块
B.
第块
C.
第块
D.
第块
如图所示,在的两边上截取,,连接AD,BC交于点P,连接OP,则下列结论正确的是
≌≌≌≌.
A.
B.
C.
D.
如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是的平分线.此角平分仪的画图原理是
A.
SSS
B.
SAS
C.
ASA
D.
AAS
如图,若≌,则下列结论中一定成立的是
A.
B.
C.
D.
经过以下变化后所得到的三角形不能和全等的是
A.
平移
B.
翻折
C.
旋转
D.
放大
如图,,D为BC的中点,其中错误的结论是
A.
≌
B.
C.
AD平分
D.
是等边三角形
二、填空题
如图,已知≌,若,,则的大小为______.
如图,点D是等边中AB边上一点,连接CD,点E在CD上,连接AE,BE,若,,,则______.
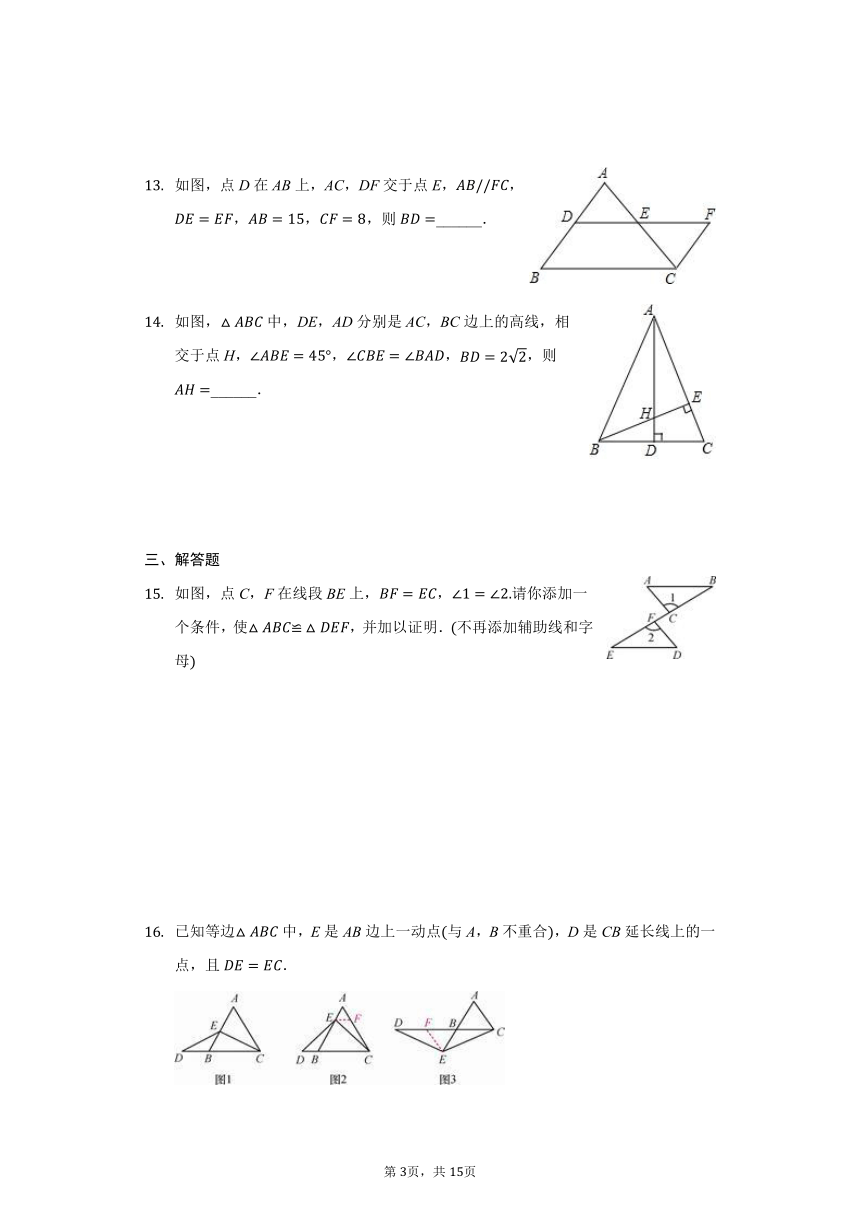
如图,点D在AB上,AC,DF交于点E,,,,,则______.
如图,中,DE,AD分别是AC,BC边上的高线,相交于点H,,,,则______.
三、解答题
如图,点C,F在线段BE上,,请你添加一个条件,使,并加以证明.不再添加辅助线和字母
已知等边中,E是AB边上一动点与A,B不重合,D是CB延长线上的一点,且.
当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AE??????????DB;填“”“”或“”
当E是AB边上任一点时,小敏与同桌小聪讨论后,认为中的结论依然成立,并进行了如下解答:
解:如图2,过点E作,交AC于点
请你按照上述思路,补充完成全部解答过程
当E是线段AB延长线上任一点时,如图中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.
如图:在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且求证:.
如图,中,,的角平分线AD、BE相交于点P,过P作交BC的延长线于点F,交AC于点H
求度数;
求证:≌;
求证:.
答案和解析
1.【答案】C
【解析】
【分析】
此题主要考查了全等三角形的判定,关键是要熟记判定定理:SSS,SAS,AAS,ASA.
根据题目中给出的条件,,要用“SAS”还缺少条件是夹角:,筛选答案可选出C.
【解答】
解:还需条件,
,
,
即:,
在和中,
≌.
故选:C.
2.【答案】D
【解析】
【分析】
此题主要考查学生对全等三角形判定定理的理解和掌握由作图过程可得,,再加上公共边可利用SSS定理判定≌.
【解答】
解:,,OC为公共边,
≌.
故选D.
3.【答案】D
【解析】
【分析】
本题考查了等腰三角形的判定及全等三角形的性质;利用全等三角形的性质是正确解答本题的关键.画出图形就能明显看出来,运用全等的性质,易解.
【解答】
解:≌
是等腰三角形.
故选D.
4.【答案】B
【解析】解:如图,≌≌≌≌≌≌,
全等且仅有1条公共边的三角形共6个,
故选:B.
根据全等三角形的判定定理,进行画图解答即可.
本题主要考查全等三角形的判定,关键在于根据判定定理画出图形.
5.【答案】B
【解析】解:带去可以利用“角边角”能配一块与原来大小一样的三角形玻璃.
故选:B.
根据三角形全等的判定方法作出判断即可.
本题考查了全等三角形的应用,是基础题,熟记三角形全等的判定方法是解题的关键.
6.【答案】A
【解析】解:,,
≌,故正确;
,
≌,故正确;
,
≌,故正确;
,
≌,故正确.
故选:A.
由,,,可证得≌,所以有,又,,可证得≌,所以有,又,,可证得≌,所以有,又,,可证得≌.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.
7.【答案】A
【解析】解:在和中,
,
≌,
,
就是的平分线,
故选:A.
由“SSS”可证≌,可得,可证AE就是的平分线,即可求解.
本题考查了全等三角形判定和性质,熟练掌握全等三角形的判定和性质是本题的关键.
8.【答案】B
【解析】解:≌,
,,,,
,
即故A,C,D选项错误,B选项正确,
故选:B.
根据全等三角形的性质即可得到结论.
本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
9.【答案】D
【解析】解:平移,旋转,翻折前后的三角形全等,
选项A,B,C不符合题意,
故选:D.
根据平移,旋转,翻折的性质即可解决问题.
本题考查几何变换综合题,全等三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10.【答案】D
【解析】解:,
,
是BC的中点,
,
在和中,
,
≌,
,,故A、B、C选项结论都正确,
只有时,是等边三角形,故D选项结论错误.
故选:D.
根据垂直的定义可得,根据线段中点的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应角相等可得,全等三角形对应角相等可得,然后选择答案即可.
本题考查了全等三角形的判定与性质,等边三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.
11.【答案】
【解析】解:≌,
,
,
故答案为:.
根据全等三角形的对应角相等求出,根据三角形的外角性质计算,得到答案.
本题考查的是全等三角形的性质、三角形的外角性质,掌握全等三角形的对应角相等是解题的关键.
12.【答案】10
【解析】解:如图,延长ED,使,连接,过点E作,
,,
是等边三角形,,
,
,且,,
≌
,,
,且,
,,
,
,
故答案为:10.
如图,延长ED,使,连接,过点E作,由“SAS”可证≌,可得,,由直角三角形的性质和勾股定理可求解.
本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的性质,勾股定理,添加恰当辅助线是本题的关键.
13.【答案】7
【解析】解:,
又,,
≌,
,
,,
.
故答案是:7.
利用,可得一组内错角相等,即,又,再加一组对顶角,利用ASA可证≌,利用全等三角形的性质可得,利用等量代换可求BD.
本题考查了全等三角形的判定及性质,利用了平行线的性质、全等三角形的判定和性质,要熟练掌握并灵活运用.
14.【答案】
【解析】解:,,
,
,
,
,
,
,
,
在和中,
,
≌,
,
,,
,
,
,
,
,
,
,
.
故答案为:.
直接利用等腰直角三角形的性质结合全等三角形的判定方法得出≌,进而得出,即可得出答案.
此题主要考查了全等三角形的判定与性质以及等腰三角形的性质等知识,正确得出是解题关键.
15.【答案】解:答案不唯一,如:,,,等.
以为例加以说明.
,
,
即.
在和中,
≌.
【解析】本题考查了全等三角形的判定的应用有关知识,先求出,添加条件,根据SAS推出两三角形全等即可.
16.【答案】;
,
,,
是等边三角形,
,即,
,
,
,,
,
在和中,
≌,
;
成立,
作交BD于F,
则易证为等边三角形,
,
,
,
,
在和中,
≌,
,
,
,即.
【解析】
【分析】
本题考查的知识点是全等三角形的判定和性质,等边三角形的判定和性质,是一道三角形的综合题.
根据等边三角形的性质、等腰三角形的三线合一证明;
证明≌,根据全等三角形的性质证明;
作交BD于F,证明≌,根据全等三角形的性质证明即可.
【解答】
解:是等边三角形,E是AB边上中点,
,,
,
,
,
,
,
,
,
故答案为:;
见答案;
见答案.
17.【答案】证明:等边三角形ABC
,
,
,
在和中,
,
≌??,
.
【解析】证明,证明≌,则结论得证.
本题考查了等边三角形的性质及全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
18.【答案】解:平分,BE平分,
,
;
,
,
,
,
在和中,
,
≌;
≌,
,,,
,
,
在和中,
,
≌,
,
,
.
【解析】根据角平分线性质可得,即可解题;
易得,可得,即可证明≌;
由结论可得,,,即可求得,即可证明≌,可得,即可解题.
本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证≌和≌是解题的关键.
第2页,共15页
第1页,共15页
一、选择题
如图,要用“SAS”证≌,若已知,,则还需具备条件
A.
B.
C.
D.
工人师傅常用角尺平分一个任意角做法如下:如图,是一个任意角,在边OA,OB上分别取,移动角尺,使角尺两边相同的刻度分别与M,N重合过角尺顶点C作射线由作法得的依据是
A.
AAS
B.
SAS
C.
ASA
D.
SSS
如果D是中BC边上一点,并且≌,则是
A.
锐角三角形
B.
钝角三角形
C.
直角三角形
D.
等腰三角形
如图,由25个同样大小的小正方形组成的正方形网格中,是格点三角形每个顶点都是格点,在这个正方形网格中画另一个格点三角形,使得它与全等且仅有一条公共边,则符合要求的三角形共能画
A.
5个
B.
6个
C.
7个
D.
8个
花花不慎将一块三角形的玻璃打碎成了如图所示的四块图中所标、、、,若要配块与原来大小一样的三角形玻璃,应该带
A.
第块
B.
第块
C.
第块
D.
第块
如图所示,在的两边上截取,,连接AD,BC交于点P,连接OP,则下列结论正确的是
≌≌≌≌.
A.
B.
C.
D.
如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是的平分线.此角平分仪的画图原理是
A.
SSS
B.
SAS
C.
ASA
D.
AAS
如图,若≌,则下列结论中一定成立的是
A.
B.
C.
D.
经过以下变化后所得到的三角形不能和全等的是
A.
平移
B.
翻折
C.
旋转
D.
放大
如图,,D为BC的中点,其中错误的结论是
A.
≌
B.
C.
AD平分
D.
是等边三角形
二、填空题
如图,已知≌,若,,则的大小为______.
如图,点D是等边中AB边上一点,连接CD,点E在CD上,连接AE,BE,若,,,则______.
如图,点D在AB上,AC,DF交于点E,,,,,则______.
如图,中,DE,AD分别是AC,BC边上的高线,相交于点H,,,,则______.
三、解答题
如图,点C,F在线段BE上,,请你添加一个条件,使,并加以证明.不再添加辅助线和字母
已知等边中,E是AB边上一动点与A,B不重合,D是CB延长线上的一点,且.
当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AE??????????DB;填“”“”或“”
当E是AB边上任一点时,小敏与同桌小聪讨论后,认为中的结论依然成立,并进行了如下解答:
解:如图2,过点E作,交AC于点
请你按照上述思路,补充完成全部解答过程
当E是线段AB延长线上任一点时,如图中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.
如图:在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且求证:.
如图,中,,的角平分线AD、BE相交于点P,过P作交BC的延长线于点F,交AC于点H
求度数;
求证:≌;
求证:.
答案和解析
1.【答案】C
【解析】
【分析】
此题主要考查了全等三角形的判定,关键是要熟记判定定理:SSS,SAS,AAS,ASA.
根据题目中给出的条件,,要用“SAS”还缺少条件是夹角:,筛选答案可选出C.
【解答】
解:还需条件,
,
,
即:,
在和中,
≌.
故选:C.
2.【答案】D
【解析】
【分析】
此题主要考查学生对全等三角形判定定理的理解和掌握由作图过程可得,,再加上公共边可利用SSS定理判定≌.
【解答】
解:,,OC为公共边,
≌.
故选D.
3.【答案】D
【解析】
【分析】
本题考查了等腰三角形的判定及全等三角形的性质;利用全等三角形的性质是正确解答本题的关键.画出图形就能明显看出来,运用全等的性质,易解.
【解答】
解:≌
是等腰三角形.
故选D.
4.【答案】B
【解析】解:如图,≌≌≌≌≌≌,
全等且仅有1条公共边的三角形共6个,
故选:B.
根据全等三角形的判定定理,进行画图解答即可.
本题主要考查全等三角形的判定,关键在于根据判定定理画出图形.
5.【答案】B
【解析】解:带去可以利用“角边角”能配一块与原来大小一样的三角形玻璃.
故选:B.
根据三角形全等的判定方法作出判断即可.
本题考查了全等三角形的应用,是基础题,熟记三角形全等的判定方法是解题的关键.
6.【答案】A
【解析】解:,,
≌,故正确;
,
≌,故正确;
,
≌,故正确;
,
≌,故正确.
故选:A.
由,,,可证得≌,所以有,又,,可证得≌,所以有,又,,可证得≌,所以有,又,,可证得≌.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.
7.【答案】A
【解析】解:在和中,
,
≌,
,
就是的平分线,
故选:A.
由“SSS”可证≌,可得,可证AE就是的平分线,即可求解.
本题考查了全等三角形判定和性质,熟练掌握全等三角形的判定和性质是本题的关键.
8.【答案】B
【解析】解:≌,
,,,,
,
即故A,C,D选项错误,B选项正确,
故选:B.
根据全等三角形的性质即可得到结论.
本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
9.【答案】D
【解析】解:平移,旋转,翻折前后的三角形全等,
选项A,B,C不符合题意,
故选:D.
根据平移,旋转,翻折的性质即可解决问题.
本题考查几何变换综合题,全等三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10.【答案】D
【解析】解:,
,
是BC的中点,
,
在和中,
,
≌,
,,故A、B、C选项结论都正确,
只有时,是等边三角形,故D选项结论错误.
故选:D.
根据垂直的定义可得,根据线段中点的定义可得,然后利用“边角边”证明和全等,根据全等三角形对应角相等可得,全等三角形对应角相等可得,然后选择答案即可.
本题考查了全等三角形的判定与性质,等边三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.
11.【答案】
【解析】解:≌,
,
,
故答案为:.
根据全等三角形的对应角相等求出,根据三角形的外角性质计算,得到答案.
本题考查的是全等三角形的性质、三角形的外角性质,掌握全等三角形的对应角相等是解题的关键.
12.【答案】10
【解析】解:如图,延长ED,使,连接,过点E作,
,,
是等边三角形,,
,
,且,,
≌
,,
,且,
,,
,
,
故答案为:10.
如图,延长ED,使,连接,过点E作,由“SAS”可证≌,可得,,由直角三角形的性质和勾股定理可求解.
本题考查了旋转的性质,全等三角形的判定和性质,等边三角形的性质,勾股定理,添加恰当辅助线是本题的关键.
13.【答案】7
【解析】解:,
又,,
≌,
,
,,
.
故答案是:7.
利用,可得一组内错角相等,即,又,再加一组对顶角,利用ASA可证≌,利用全等三角形的性质可得,利用等量代换可求BD.
本题考查了全等三角形的判定及性质,利用了平行线的性质、全等三角形的判定和性质,要熟练掌握并灵活运用.
14.【答案】
【解析】解:,,
,
,
,
,
,
,
,
在和中,
,
≌,
,
,,
,
,
,
,
,
,
,
.
故答案为:.
直接利用等腰直角三角形的性质结合全等三角形的判定方法得出≌,进而得出,即可得出答案.
此题主要考查了全等三角形的判定与性质以及等腰三角形的性质等知识,正确得出是解题关键.
15.【答案】解:答案不唯一,如:,,,等.
以为例加以说明.
,
,
即.
在和中,
≌.
【解析】本题考查了全等三角形的判定的应用有关知识,先求出,添加条件,根据SAS推出两三角形全等即可.
16.【答案】;
,
,,
是等边三角形,
,即,
,
,
,,
,
在和中,
≌,
;
成立,
作交BD于F,
则易证为等边三角形,
,
,
,
,
在和中,
≌,
,
,
,即.
【解析】
【分析】
本题考查的知识点是全等三角形的判定和性质,等边三角形的判定和性质,是一道三角形的综合题.
根据等边三角形的性质、等腰三角形的三线合一证明;
证明≌,根据全等三角形的性质证明;
作交BD于F,证明≌,根据全等三角形的性质证明即可.
【解答】
解:是等边三角形,E是AB边上中点,
,,
,
,
,
,
,
,
,
故答案为:;
见答案;
见答案.
17.【答案】证明:等边三角形ABC
,
,
,
在和中,
,
≌??,
.
【解析】证明,证明≌,则结论得证.
本题考查了等边三角形的性质及全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
18.【答案】解:平分,BE平分,
,
;
,
,
,
,
在和中,
,
≌;
≌,
,,,
,
,
在和中,
,
≌,
,
,
.
【解析】根据角平分线性质可得,即可解题;
易得,可得,即可证明≌;
由结论可得,,,即可求得,即可证明≌,可得,即可解题.
本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证≌和≌是解题的关键.
第2页,共15页
第1页,共15页
同课章节目录
