人教版八年级上册数学 12.2 三角形全等的判定 同步习题(word版,含答案)
文档属性
| 名称 | 人教版八年级上册数学 12.2 三角形全等的判定 同步习题(word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 132.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 00:00:00 | ||
图片预览


文档简介
12.2 三角形全等的判定 同步习题
一.选择题
1.如图,已知AC=AD,再添加一个条件仍不能判定△ABC≌△ABD的是( )
A.∠C=∠D=90° B.∠BAC=∠BAD C.BC=BD D.∠ABC=∠ABD
2.一块三角形玻璃被打碎后,店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃,能够全等的依据是( )
A.ASA B.AAS C.SAS D.SSS
3.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容
则回答正确的是( )
A.?代表对应边 B.※代表110°
C.@代表ASA D.◎代表∠DCA
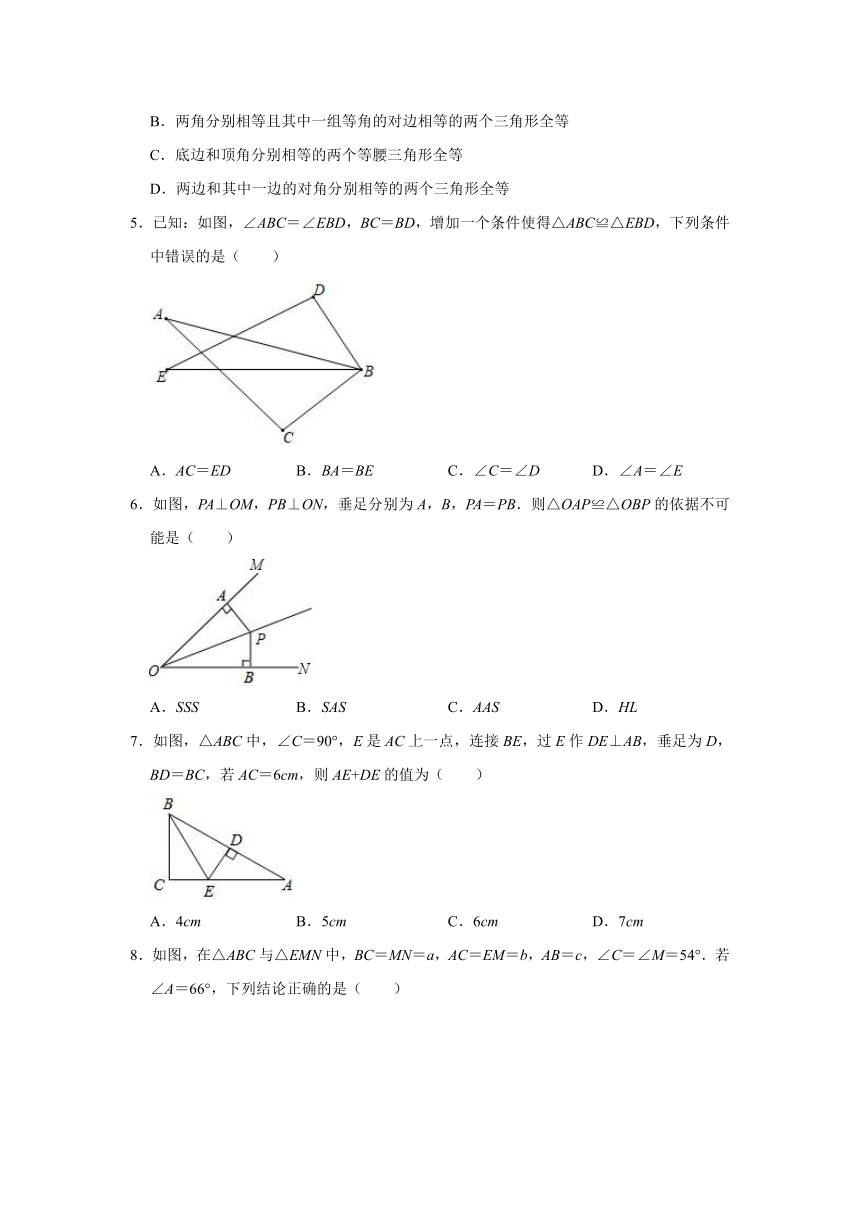
4.下列说法不正确的是( )
A.两边和它们的夹角分别相等的两个三角形全等
B.两角分别相等且其中一组等角的对边相等的两个三角形全等
C.底边和顶角分别相等的两个等腰三角形全等
D.两边和其中一边的对角分别相等的两个三角形全等
5.已知:如图,∠ABC=∠EBD,BC=BD,增加一个条件使得△ABC≌△EBD,下列条件中错误的是( )
A.AC=ED B.BA=BE C.∠C=∠D D.∠A=∠E
6.如图,PA⊥OM,PB⊥ON,垂足分别为A,B,PA=PB.则△OAP≌△OBP的依据不可能是( )
A.SSS B.SAS C.AAS D.HL
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm B.5cm C.6cm D.7cm
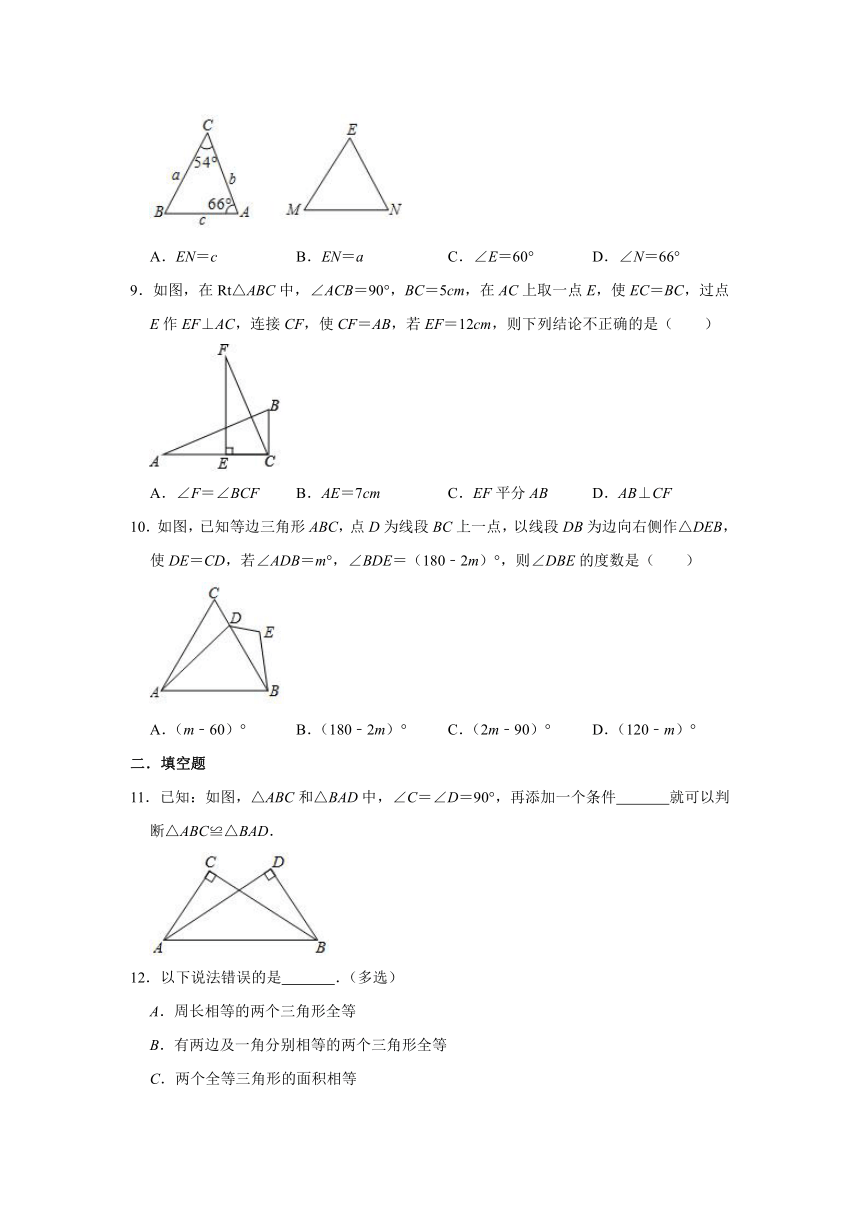
8.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是( )
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
9.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
10.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)° B.(180﹣2m)° C.(2m﹣90)° D.(120﹣m)°
二.填空题
11.已知:如图,△ABC和△BAD中,∠C=∠D=90°,再添加一个条件 就可以判断△ABC≌△BAD.
12.以下说法错误的是 .(多选)
A.周长相等的两个三角形全等
B.有两边及一角分别相等的两个三角形全等
C.两个全等三角形的面积相等
D.面积相等的两个三角形全等
13.在△ABC中,AB=AC,∠ABC=∠ACB,CE是高,且∠ECA=36°,平面内有一异于点A,B,C,E的点D,若△ABC≌△CDA,则∠DAE的度数为 .
14.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是 秒.
15.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
三.解答题
16.如图,△ABC中,AB=AC,点D,E在边BC上,BD=CE.求证:∠ADE=∠AED.
17.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
18.在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌AFE;
(2)AD=AB+CD;
参考答案
1.D
2.A
3.B
4.D
5.A
6.A.
7.C
8.A
9.C
10.A
11.AC=BD
12.A、B、D
13.117°、27°、9°和81°.
14.4
15.①③④
16.证明:∵AB=AC,
∴∠B=∠C(等边对等角),
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴AD=AE(全等三角形对应边相等),
∴∠ADE=∠AED(等边对等角).
17.解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
18.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,
∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,
,
∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
一.选择题
1.如图,已知AC=AD,再添加一个条件仍不能判定△ABC≌△ABD的是( )
A.∠C=∠D=90° B.∠BAC=∠BAD C.BC=BD D.∠ABC=∠ABD
2.一块三角形玻璃被打碎后,店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃,能够全等的依据是( )
A.ASA B.AAS C.SAS D.SSS
3.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容
则回答正确的是( )
A.?代表对应边 B.※代表110°
C.@代表ASA D.◎代表∠DCA
4.下列说法不正确的是( )
A.两边和它们的夹角分别相等的两个三角形全等
B.两角分别相等且其中一组等角的对边相等的两个三角形全等
C.底边和顶角分别相等的两个等腰三角形全等
D.两边和其中一边的对角分别相等的两个三角形全等
5.已知:如图,∠ABC=∠EBD,BC=BD,增加一个条件使得△ABC≌△EBD,下列条件中错误的是( )
A.AC=ED B.BA=BE C.∠C=∠D D.∠A=∠E
6.如图,PA⊥OM,PB⊥ON,垂足分别为A,B,PA=PB.则△OAP≌△OBP的依据不可能是( )
A.SSS B.SAS C.AAS D.HL
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm B.5cm C.6cm D.7cm
8.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是( )
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
9.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF
10.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)° B.(180﹣2m)° C.(2m﹣90)° D.(120﹣m)°
二.填空题
11.已知:如图,△ABC和△BAD中,∠C=∠D=90°,再添加一个条件 就可以判断△ABC≌△BAD.
12.以下说法错误的是 .(多选)
A.周长相等的两个三角形全等
B.有两边及一角分别相等的两个三角形全等
C.两个全等三角形的面积相等
D.面积相等的两个三角形全等
13.在△ABC中,AB=AC,∠ABC=∠ACB,CE是高,且∠ECA=36°,平面内有一异于点A,B,C,E的点D,若△ABC≌△CDA,则∠DAE的度数为 .
14.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是 秒.
15.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
三.解答题
16.如图,△ABC中,AB=AC,点D,E在边BC上,BD=CE.求证:∠ADE=∠AED.
17.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
18.在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌AFE;
(2)AD=AB+CD;
参考答案
1.D
2.A
3.B
4.D
5.A
6.A.
7.C
8.A
9.C
10.A
11.AC=BD
12.A、B、D
13.117°、27°、9°和81°.
14.4
15.①③④
16.证明:∵AB=AC,
∴∠B=∠C(等边对等角),
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴AD=AE(全等三角形对应边相等),
∴∠ADE=∠AED(等边对等角).
17.解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
18.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,
∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,
,
∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
