直线与圆的位置关系

(共12张PPT)
执教者：郑海兵
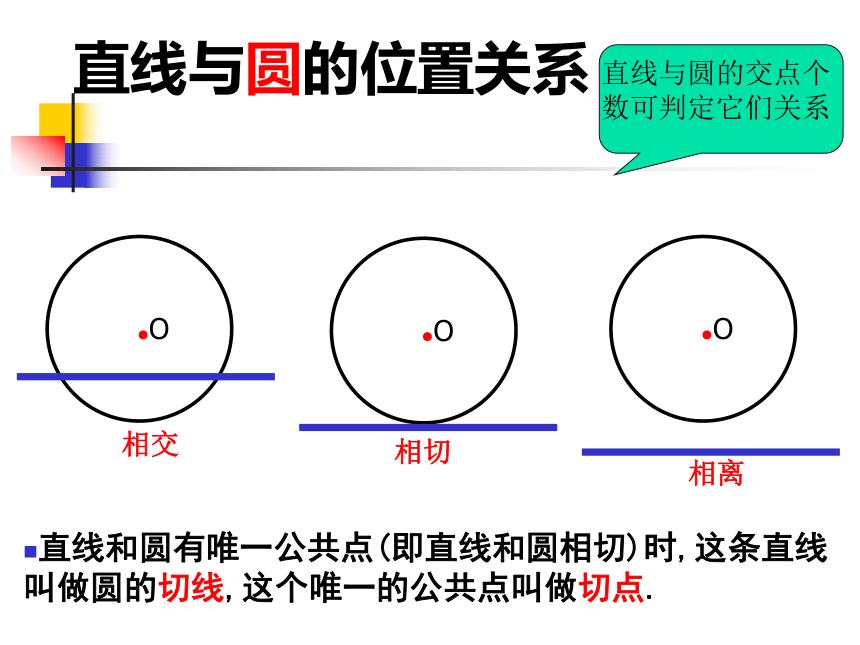
直线与圆的位置关系
●O
●O
相交
直线和圆有唯一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
●O
相切
相离
直线与圆的交点个数可判定它们关系
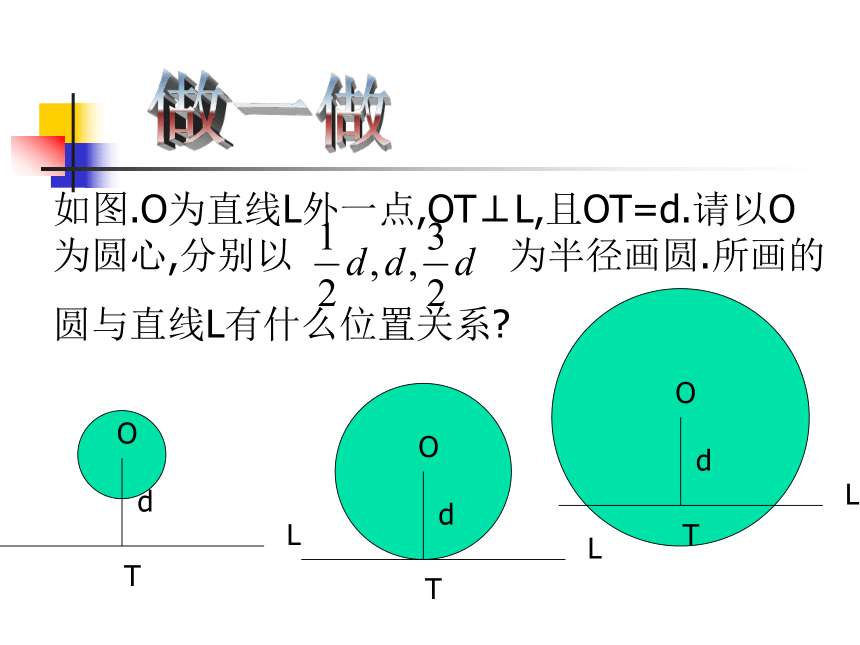
如图.O为直线L外一点,OT⊥L,且OT=d.请以O为圆心,分别以 为半径画圆.所画的
圆与直线L有什么位置关系
L
T
O
d
L
T
O
d
L
T
O
d
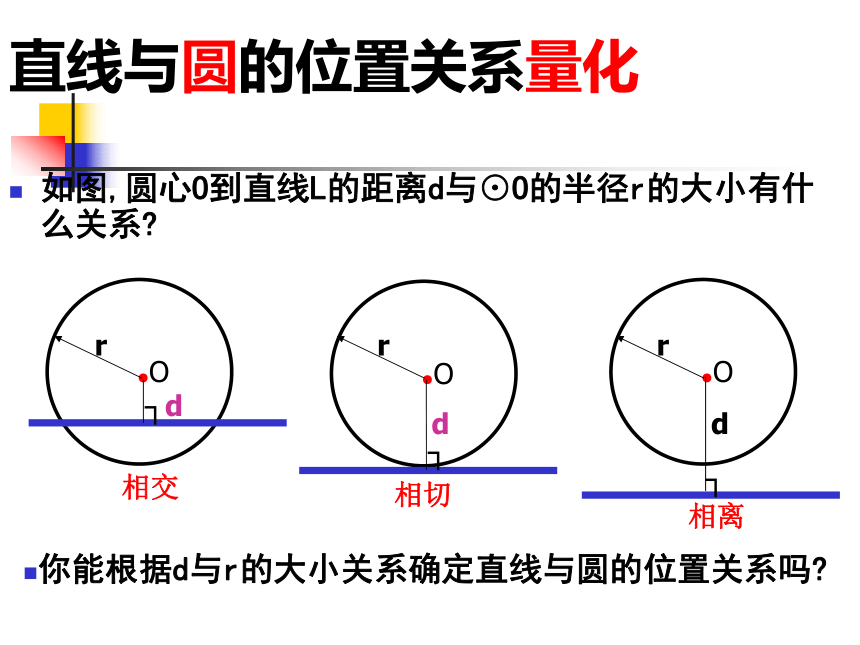
如图,圆心O到直线L的距离d与⊙O的半径r的大小有什么关系
你能根据d与r的大小关系确定直线与圆的位置关系吗
●O
●O
相交
●O
相切
相离
直线与圆的位置关系量化
r
r
r
┐d
d
┐
d
┐
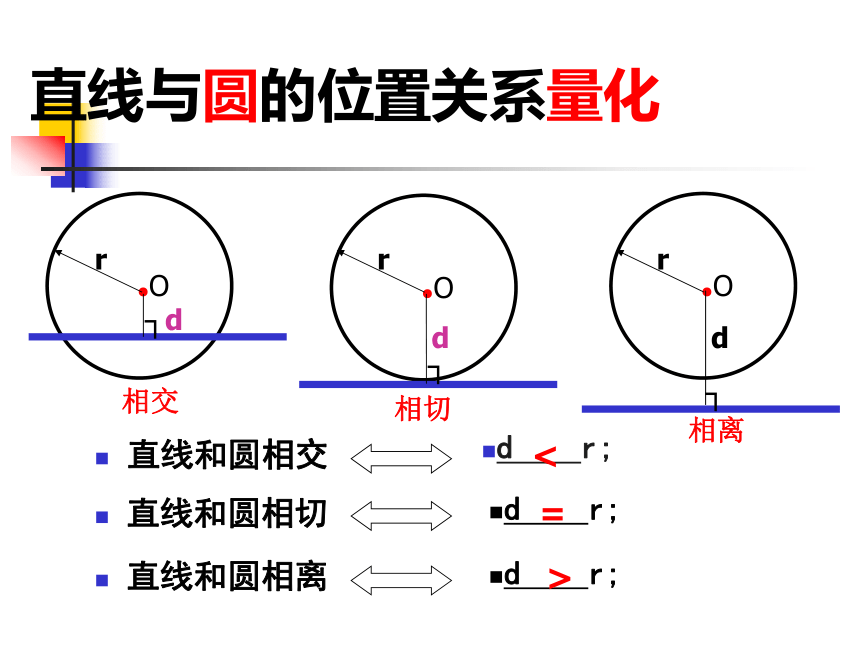
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系量化
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
设⊙O的半径为r，圆心O到直线L的距离为d，根据下列条件判断直线L与⊙O的位置关系:
d=4，r=3 (2)d=1，r= (3)
(4)
解：
（1）∵d>r,
∴直线 与⊙O相离.
（2）∵d∴直线 与⊙O相交.
（4）∵d=r,
∴直线 与⊙O相切.
（3）∵d>r,
∴直线 与⊙O相离.
已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆,当半径为多长时,AB与⊙C相切
A
C
B
┐
D
┛
例1；
解：作CD⊥AB于点D.
∵S△ABC=AC×BC÷2=AB×CD÷2
8
4
∴CD=AC×BC÷AB=
∴ AB与⊙C相切.
在直角三角形ABC 中，∠ACB=90°，CA=3，CB=4.设⊙C 的半径为r. 请根据r的下列值，判断AB与⊙C 的位置关系，并说明理由.
(1) r=2 (2) r=2.4 (3) r=3
A
C
B
┐
D
┛
3
4
解：作CD⊥AB于点D.
AB=5, CD=3×4÷5=2.4
（1）∵r＜CD, ∴直线AB与⊙C相离.
（2）∵r=CD, ∴直线AB与⊙C相切.
（3）∵r＞CD, ∴直线AB与⊙C相交.
1、船有无触礁的危险
如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.
请与同伴交流你是怎么想的 怎么去做
你认为货轮继续向东航行途中会有触礁的危险吗
P
A
B
H
北
例2；
600
450
10
解：作PH⊥AB于点H.
由题可得 ∠PAH=30○ , ∠PBH=45○
∴货轮没有触礁的危险。
P
A
B
H
北
600
450
10
如图,海中有一个小岛P,该岛四周12海里内暗礁.今有一货轮由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航 行.你认为货轮继续向东航行途中会有触礁的危险吗
直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O

d
r
O
l

d
r
O

d
r