圆的对称性1
图片预览




文档简介
(共14张PPT)
沪科版九年级下
执教者:郑海兵
第3章
圆
观察自行车的车轮和转盘以及链条,你能说出车轮、转盘的特征吗?它们与链条之间有怎样的关系呢?
这就是圆的一种原型.
本章要研究的是圆的性质、直线与圆、圆与圆的位置关系.
3.1.1 圆的对称性
如图是国际奥林匹克运动会旗的标志图案.
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径.
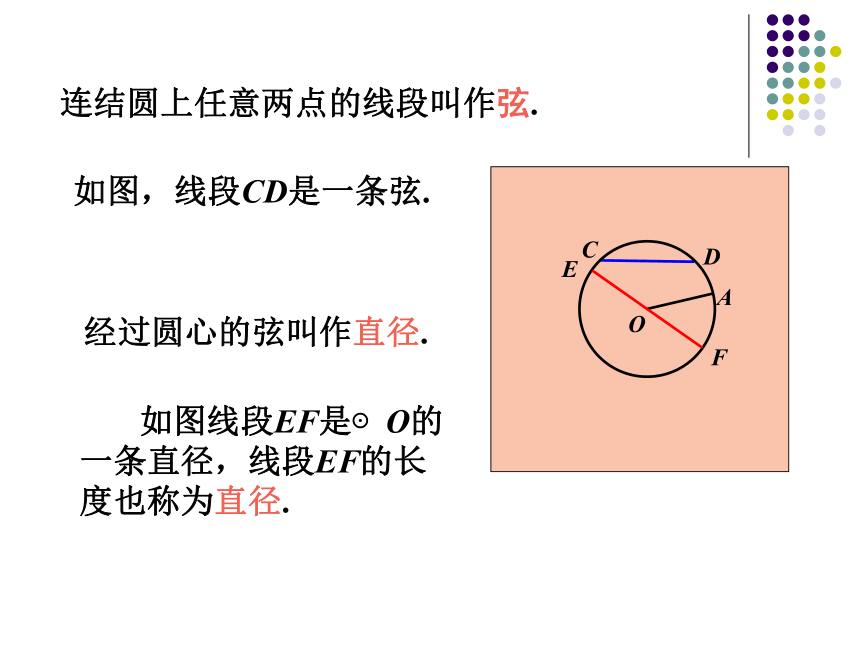
如图线段EF是⊙O的一条直径,线段EF的长度也称为直径.
连结圆上任意两点的线段叫作弦.
如图,线段CD是一条弦.
经过圆心的弦叫作直径.
·
O
A
D
C
E
F
这两个圆
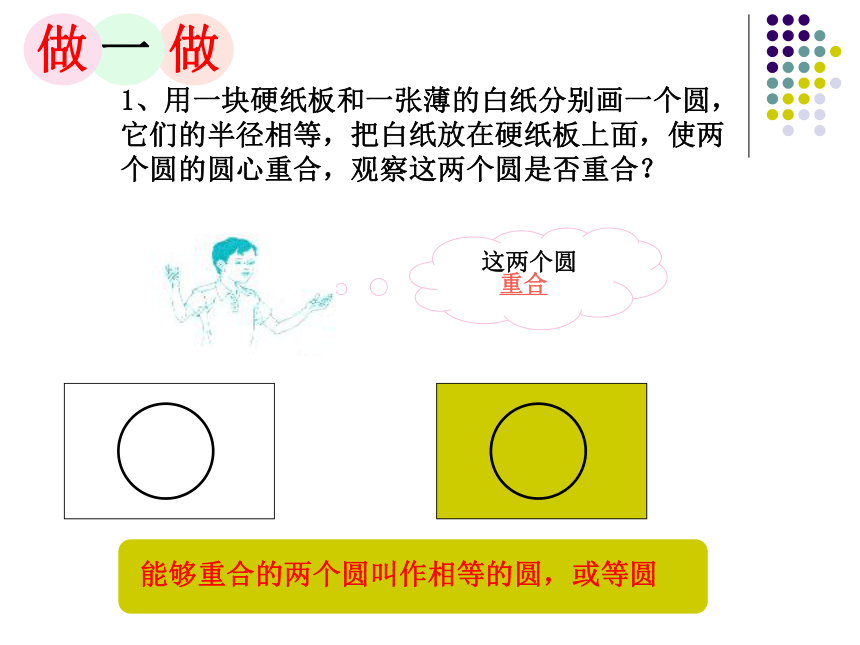
1、用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
做
一
做
能够重合的两个圆叫作相等的圆,或等圆
重合
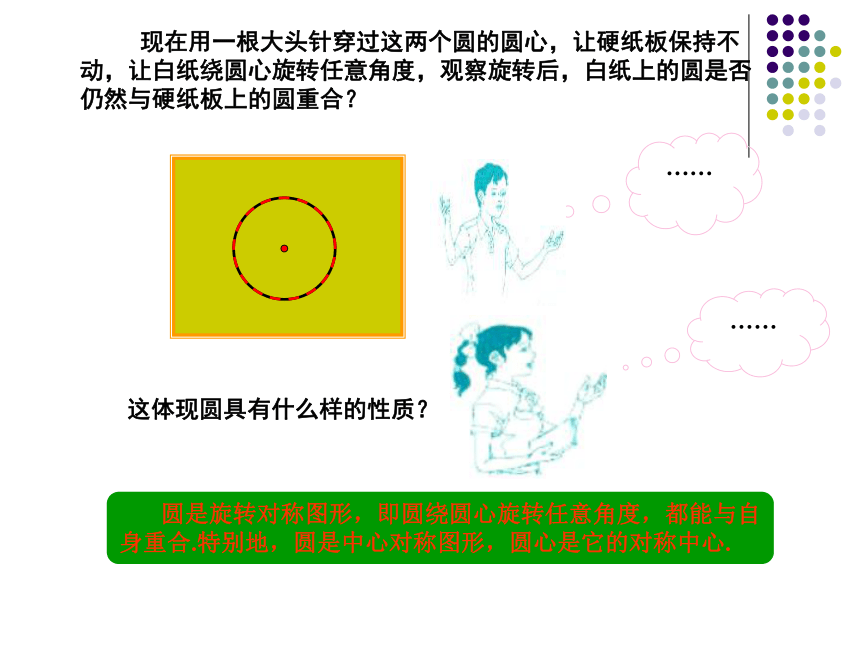
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
这体现圆具有什么样的性质?
……
……
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合.特别地,圆是中心对称图形,圆心是它的对称中心.
·
2.在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
这体现圆具有什么样的对称性?
……
你能讲出圆具有这种对称性的道理吗?
定理1 垂直于弦的直径平分这条弦.
……
证明:
现在你能说出道理吗
·
O
B
A
D
C
E
如图,在⊙O中,直径CD与弦AB垂直,
垂足为E,连结OA,OB.
由于,OA=OB
因此△OAB是等腰三角形.
又OE是底边AB上的高,
因而OE也是底边AB上的中线,
从而AE=BE.
为什么圆的任意一条直径所在的直线是它的对称轴
?
?
定理1 垂直于弦的直径平分这条弦.
P是⊙O上任意一点,
于是点P与点Q关于直线EF对称,因此,圆O关于直线EF对称.
这样我们证明了圆还有下述性质:
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
根据定理1,EF平分弦PQ,从而直线EF是线段PQ的垂直平分线.
·
O
P
F
E
Q
M
如图,EF是⊙O的任意一条直径,
直线EF与线段PQ的关系如何?
过点P作EF的垂线,与⊙O交点Q,
1、自行车的车轱辘是圆形,为什么?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
练 习
3. 已知⊙O的半径为5cm,弦AB的长为6cm求圆心到AB的
距离.
练习
如图作OD⊥AB垂足为D
在Rt △ ADO中
∴ OD=4
∴圆心到AB的距离为4㎝
·
A
B
O
D
连结OA
2.下述命题是否正确?为什么?
(1)平分弦(不是直径)的直径垂直于这条弦;
(2)圆只有一条对称轴.
根据垂径定理
有无数条对称轴
任意一条直径所在的直线都是它的对称轴.
正确
错
沪科版九年级下
执教者:郑海兵
第3章
圆
观察自行车的车轮和转盘以及链条,你能说出车轮、转盘的特征吗?它们与链条之间有怎样的关系呢?
这就是圆的一种原型.
本章要研究的是圆的性质、直线与圆、圆与圆的位置关系.
3.1.1 圆的对称性
如图是国际奥林匹克运动会旗的标志图案.
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径.
如图线段EF是⊙O的一条直径,线段EF的长度也称为直径.
连结圆上任意两点的线段叫作弦.
如图,线段CD是一条弦.
经过圆心的弦叫作直径.
·
O
A
D
C
E
F
这两个圆
1、用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
做
一
做
能够重合的两个圆叫作相等的圆,或等圆
重合
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
这体现圆具有什么样的性质?
……
……
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合.特别地,圆是中心对称图形,圆心是它的对称中心.
·
2.在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
这体现圆具有什么样的对称性?
……
你能讲出圆具有这种对称性的道理吗?
定理1 垂直于弦的直径平分这条弦.
……
证明:
现在你能说出道理吗
·
O
B
A
D
C
E
如图,在⊙O中,直径CD与弦AB垂直,
垂足为E,连结OA,OB.
由于,OA=OB
因此△OAB是等腰三角形.
又OE是底边AB上的高,
因而OE也是底边AB上的中线,
从而AE=BE.
为什么圆的任意一条直径所在的直线是它的对称轴
?
?
定理1 垂直于弦的直径平分这条弦.
P是⊙O上任意一点,
于是点P与点Q关于直线EF对称,因此,圆O关于直线EF对称.
这样我们证明了圆还有下述性质:
圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
根据定理1,EF平分弦PQ,从而直线EF是线段PQ的垂直平分线.
·
O
P
F
E
Q
M
如图,EF是⊙O的任意一条直径,
直线EF与线段PQ的关系如何?
过点P作EF的垂线,与⊙O交点Q,
1、自行车的车轱辘是圆形,为什么?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
练 习
3. 已知⊙O的半径为5cm,弦AB的长为6cm求圆心到AB的
距离.
练习
如图作OD⊥AB垂足为D
在Rt △ ADO中
∴ OD=4
∴圆心到AB的距离为4㎝
·
A
B
O
D
连结OA
2.下述命题是否正确?为什么?
(1)平分弦(不是直径)的直径垂直于这条弦;
(2)圆只有一条对称轴.
根据垂径定理
有无数条对称轴
任意一条直径所在的直线都是它的对称轴.
正确
错
