华师大新版七年级(上)数学 第5章 相交线与平行线 单元测试卷 (word版,含解析)
文档属性
| 名称 | 华师大新版七年级(上)数学 第5章 相交线与平行线 单元测试卷 (word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 674.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 06:31:44 | ||
图片预览



文档简介
第5章 相交线与平行线 单元测试卷
一、选择题(共10小题).
1.a、b、c是同一平面内的任意三条直线,其交点个数有( )
A.1或2个 B.1或2或3个
C.0或1或3个 D.0或1或2或3个
2.如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
3.如图,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
4.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3 B.PQ>3 C.PQ=3 D.PQ<3
5.如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
A.40° B.50° C.60° D.70°
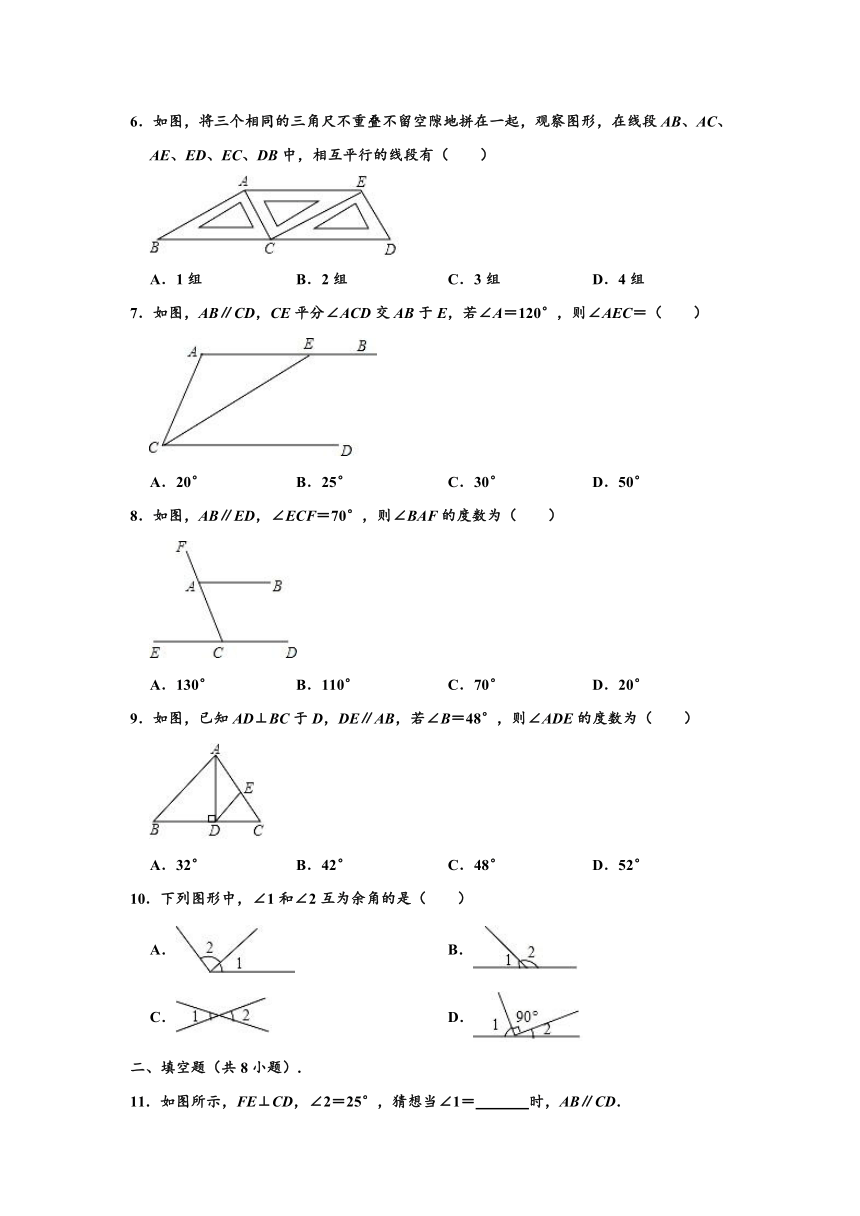
6.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
A.1组 B.2组 C.3组 D.4组
7.如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
A.20° B.25° C.30° D.50°
8.如图,AB∥ED,∠ECF=70°,则∠BAF的度数为( )
A.130° B.110° C.70° D.20°
9.如图,已知AD⊥BC于D,DE∥AB,若∠B=48°,则∠ADE的度数为( )
A.32° B.42° C.48° D.52°
10.下列图形中,∠1和∠2互为余角的是( )
A. B.
C. D.
二、填空题(共8小题).
11.如图所示,FE⊥CD,∠2=25°,猜想当∠1= 时,AB∥CD.
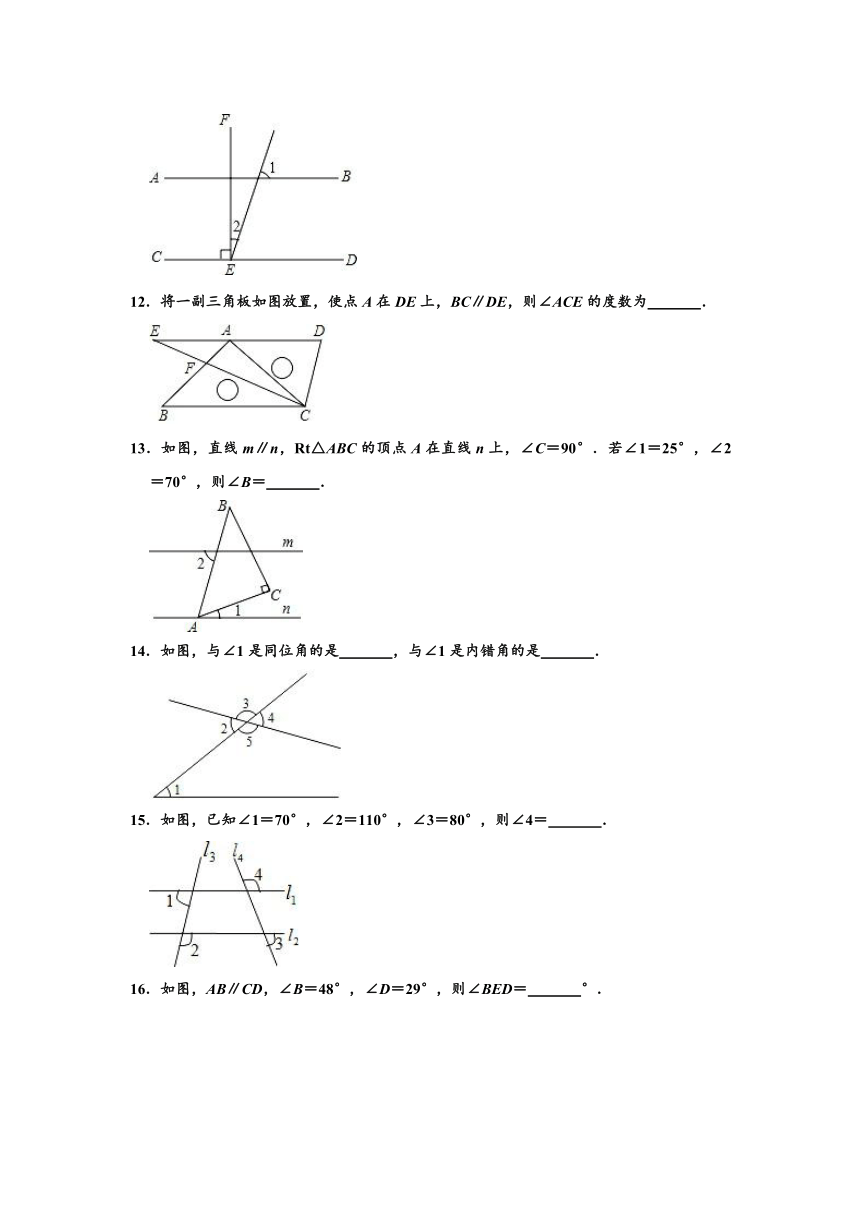
12.将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为 .
13.如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B= .
14.如图,与∠1是同位角的是 ,与∠1是内错角的是 .
15.如图,已知∠1=70°,∠2=110°,∠3=80°,则∠4= .
16.如图,AB∥CD,∠B=48°,∠D=29°,则∠BED= °.
17.上午8点时,时针与分针的夹角是 度.
18.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为 °.
三、计算题(本大题共3小题,共18分)
19.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
20.如图,直线AB、CD相交于点O,射线OM,ON分别平分∠AOC,∠AOD,求∠MON的度数.
21.(1)①如图1,已知AB∥CD,∠ABC=60°,根据 可得∠BCD= °;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM= °;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN= °.
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
四、解答题(本大题共4小题,共28分)
22.如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.
24.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
25.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案
一、选择题(本大题共10小题,共30分)
1.a、b、c是同一平面内的任意三条直线,其交点个数有( )
A.1或2个 B.1或2或3个
C.0或1或3个 D.0或1或2或3个
解:由题意画出图形,如图所示:
故选:D.
2.如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
3.如图,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
解:∠1与∠2是内错角,
故选:C.
4.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3 B.PQ>3 C.PQ=3 D.PQ<3
解:∵点P到MN的距离为3,Q是直线MN上的任意一点,
∴PQ≥3,
故选:A.
5.如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
A.40° B.50° C.60° D.70°
解:∵AB∥DE,∠CDE=40°,
∴∠B=∠CDE=40°,
又∵FG⊥BC,
∴∠FGB=90°﹣∠B=50°,
故选:B.
6.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
A.1组 B.2组 C.3组 D.4组
解:∠B=∠DCE,则AB∥EC(同位角相等,两直线平行);
∠ACE=∠DEC,则AC∥DE(内错角相等,两直线平行).
∠EAC+∠ACD=180°,则AE∥DB(同旁内角互补,两直线平行).
则线段AB、AC、AE、ED、EC、DB中,相互平行的线段有:AB∥EC,AC∥DE,AE∥DB共3组.
故选:C.
7.如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
A.20° B.25° C.30° D.50°
解:∵AB∥CD,∠A=120°,
∴∠ACD=60°,
∵CE平分∠ACD,
∴∠ECD=∠AEC=30°,
∵AB∥CD,
∴∠AEC=∠ECD=30°,
故选:C.
8.如图,AB∥ED,∠ECF=70°,则∠BAF的度数为( )
A.130° B.110° C.70° D.20°
解:∵AB∥ED,
∴∠BAC=∠ECF,又∠ECF=70°,
∴∠BAC=70°,
则∠BAF=180°﹣∠BAC=180°﹣70°=110°.
故选:B.
9.如图,已知AD⊥BC于D,DE∥AB,若∠B=48°,则∠ADE的度数为( )
A.32° B.42° C.48° D.52°
解:∵DE∥AB,
∴∠EDC=∠B=48°,
∵AD⊥BC,
∴∠ADE=90°﹣48°=42°,
故选:B.
10.下列图形中,∠1和∠2互为余角的是( )
A. B.
C. D.
解:A、∠1+∠2>90°,∠1和∠2不是互为余角,故本选项错误;
B、∠1和∠2互为邻补角,故本选项错误;
C、∠1和∠2是对顶角,不是互为余角,故本选项错误;
D、∠1+∠2=180°﹣90°=90°,∠1和∠2互为余角,故本选项正确.
故选:D.
二、填空题(本大题共8小题,共24分)
11.如图所示,FE⊥CD,∠2=25°,猜想当∠1= 65° 时,AB∥CD.
解:∵FE⊥CD,∠2=25°,
∴∠NED=65°,
当∠1=65°时,
则AB∥CD.
故答案为:65°.
12.将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为 15° .
解:∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACE=∠ACB﹣∠BCE=45°﹣30°=15°,
故答案为:15°.
13.如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B= 45° .
解:∵m∥n,
∴∠3=∠2=70°,
∴∠BAC=∠3﹣∠1=70°﹣25°=45°,
∵∠C=90°,
∴∠B=90°﹣∠BAC=90°﹣45°=45°.
故答案为:45°.
14.如图,与∠1是同位角的是 ∠4 ,与∠1是内错角的是 ∠2 .
解:与∠1是同位角的是∠4,与∠1是内错角的是∠2,
故答案为:∠4;∠2.
15.如图,已知∠1=70°,∠2=110°,∠3=80°,则∠4= 100° .
解:∵∠2+∠5=180°,∠2=110°,
∴∠5=70°,又∠1=70°,
∴∠5=∠1,
∴l1∥l2,
∴∠6=∠3=80°,
∵∠4+∠6=180°,
∴∠4=100°.
故答案为:100°.
16.如图,AB∥CD,∠B=48°,∠D=29°,则∠BED= 77 °.
解:过E作EF∥AB,
∵AB∥CD,
∴∠BEF=∠B=48°,∠DEF=∠D=29°,
∴∠BED=∠BEF+∠DEF=48°+29°=77°,
故答案为:77.
17.上午8点时,时针与分针的夹角是 120 度.
解:上午8点时,分针指向数字12,时针指向数字8,所以时针与分针的夹角=4×30°=120°.
故答案为120.
18.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为 50 °.
解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+20°=50°,
故答案为:50
三、计算题(本大题共3小题,共18分)
19.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
解:(1)∵OA平分∠EOC,
∴∠AOC=∠EOC=×70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC=∠EOC=×72°=36°,
∴∠BOD=∠AOC=36°.
20.如图,直线AB、CD相交于点O,射线OM,ON分别平分∠AOC,∠AOD,求∠MON的度数.
【解答】证明:∵射线OM,ON分别平分∠AOC,∠AOD,
∴∠AOM=∠AOC,∠AON=∠AOD.
∴∠AOM+∠AON=(∠AOC+∠AOD),
即∠MON=∠COD.
∵∠COD=180°,
∴∠MON=∠COD=×180°=90°.
∴OM⊥ON.
21.(1)①如图1,已知AB∥CD,∠ABC=60°,根据 两直线平行,内错角相等 可得∠BCD= 60 °;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM= 30 °;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN= 60 °.
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
解:(1)①两直线平行,内错角相等;60;
②30;
③60.
(2)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,
∴∠BCN=140°÷2=70°.
∵CN⊥CM,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
四、解答题(本大题共4小题,共28分)
22.如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.
解:∵BE⊥AC,
∴∠BEC=90°,
∵DF∥BE,
∴∠BEC=∠DFC=90°,
∵∠C=64°,
∴∠FDC=180°﹣(∠DFC+∠C)
=180°﹣(90°+64°)
=26°,
∵∠ABC=36°,∠C=64°,
∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣36°﹣64°=80°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=×80°=40°,
∴∠AHB=∠DAC+∠BEA
=40°+90°
=130°.
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.
解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠DAC=∠EAD=30°,
又∵AD∥BC,
∴∠C=∠DAC=30°.
24.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
解:如图,∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、
AC被直线BC所截形成的同位角.
25.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
【解答】证明:过E作EF∥AB 交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
一、选择题(共10小题).
1.a、b、c是同一平面内的任意三条直线,其交点个数有( )
A.1或2个 B.1或2或3个
C.0或1或3个 D.0或1或2或3个
2.如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
3.如图,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
4.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3 B.PQ>3 C.PQ=3 D.PQ<3
5.如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
A.40° B.50° C.60° D.70°
6.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
A.1组 B.2组 C.3组 D.4组
7.如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
A.20° B.25° C.30° D.50°
8.如图,AB∥ED,∠ECF=70°,则∠BAF的度数为( )
A.130° B.110° C.70° D.20°
9.如图,已知AD⊥BC于D,DE∥AB,若∠B=48°,则∠ADE的度数为( )
A.32° B.42° C.48° D.52°
10.下列图形中,∠1和∠2互为余角的是( )
A. B.
C. D.
二、填空题(共8小题).
11.如图所示,FE⊥CD,∠2=25°,猜想当∠1= 时,AB∥CD.
12.将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为 .
13.如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B= .
14.如图,与∠1是同位角的是 ,与∠1是内错角的是 .
15.如图,已知∠1=70°,∠2=110°,∠3=80°,则∠4= .
16.如图,AB∥CD,∠B=48°,∠D=29°,则∠BED= °.
17.上午8点时,时针与分针的夹角是 度.
18.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为 °.
三、计算题(本大题共3小题,共18分)
19.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
20.如图,直线AB、CD相交于点O,射线OM,ON分别平分∠AOC,∠AOD,求∠MON的度数.
21.(1)①如图1,已知AB∥CD,∠ABC=60°,根据 可得∠BCD= °;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM= °;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN= °.
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
四、解答题(本大题共4小题,共28分)
22.如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.
24.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
25.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案
一、选择题(本大题共10小题,共30分)
1.a、b、c是同一平面内的任意三条直线,其交点个数有( )
A.1或2个 B.1或2或3个
C.0或1或3个 D.0或1或2或3个
解:由题意画出图形,如图所示:
故选:D.
2.如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
3.如图,∠1和∠2是一对( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
解:∠1与∠2是内错角,
故选:C.
4.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3 B.PQ>3 C.PQ=3 D.PQ<3
解:∵点P到MN的距离为3,Q是直线MN上的任意一点,
∴PQ≥3,
故选:A.
5.如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
A.40° B.50° C.60° D.70°
解:∵AB∥DE,∠CDE=40°,
∴∠B=∠CDE=40°,
又∵FG⊥BC,
∴∠FGB=90°﹣∠B=50°,
故选:B.
6.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
A.1组 B.2组 C.3组 D.4组
解:∠B=∠DCE,则AB∥EC(同位角相等,两直线平行);
∠ACE=∠DEC,则AC∥DE(内错角相等,两直线平行).
∠EAC+∠ACD=180°,则AE∥DB(同旁内角互补,两直线平行).
则线段AB、AC、AE、ED、EC、DB中,相互平行的线段有:AB∥EC,AC∥DE,AE∥DB共3组.
故选:C.
7.如图,AB∥CD,CE平分∠ACD交AB于E,若∠A=120°,则∠AEC=( )
A.20° B.25° C.30° D.50°
解:∵AB∥CD,∠A=120°,
∴∠ACD=60°,
∵CE平分∠ACD,
∴∠ECD=∠AEC=30°,
∵AB∥CD,
∴∠AEC=∠ECD=30°,
故选:C.
8.如图,AB∥ED,∠ECF=70°,则∠BAF的度数为( )
A.130° B.110° C.70° D.20°
解:∵AB∥ED,
∴∠BAC=∠ECF,又∠ECF=70°,
∴∠BAC=70°,
则∠BAF=180°﹣∠BAC=180°﹣70°=110°.
故选:B.
9.如图,已知AD⊥BC于D,DE∥AB,若∠B=48°,则∠ADE的度数为( )
A.32° B.42° C.48° D.52°
解:∵DE∥AB,
∴∠EDC=∠B=48°,
∵AD⊥BC,
∴∠ADE=90°﹣48°=42°,
故选:B.
10.下列图形中,∠1和∠2互为余角的是( )
A. B.
C. D.
解:A、∠1+∠2>90°,∠1和∠2不是互为余角,故本选项错误;
B、∠1和∠2互为邻补角,故本选项错误;
C、∠1和∠2是对顶角,不是互为余角,故本选项错误;
D、∠1+∠2=180°﹣90°=90°,∠1和∠2互为余角,故本选项正确.
故选:D.
二、填空题(本大题共8小题,共24分)
11.如图所示,FE⊥CD,∠2=25°,猜想当∠1= 65° 时,AB∥CD.
解:∵FE⊥CD,∠2=25°,
∴∠NED=65°,
当∠1=65°时,
则AB∥CD.
故答案为:65°.
12.将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为 15° .
解:∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACE=∠ACB﹣∠BCE=45°﹣30°=15°,
故答案为:15°.
13.如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B= 45° .
解:∵m∥n,
∴∠3=∠2=70°,
∴∠BAC=∠3﹣∠1=70°﹣25°=45°,
∵∠C=90°,
∴∠B=90°﹣∠BAC=90°﹣45°=45°.
故答案为:45°.
14.如图,与∠1是同位角的是 ∠4 ,与∠1是内错角的是 ∠2 .
解:与∠1是同位角的是∠4,与∠1是内错角的是∠2,
故答案为:∠4;∠2.
15.如图,已知∠1=70°,∠2=110°,∠3=80°,则∠4= 100° .
解:∵∠2+∠5=180°,∠2=110°,
∴∠5=70°,又∠1=70°,
∴∠5=∠1,
∴l1∥l2,
∴∠6=∠3=80°,
∵∠4+∠6=180°,
∴∠4=100°.
故答案为:100°.
16.如图,AB∥CD,∠B=48°,∠D=29°,则∠BED= 77 °.
解:过E作EF∥AB,
∵AB∥CD,
∴∠BEF=∠B=48°,∠DEF=∠D=29°,
∴∠BED=∠BEF+∠DEF=48°+29°=77°,
故答案为:77.
17.上午8点时,时针与分针的夹角是 120 度.
解:上午8点时,分针指向数字12,时针指向数字8,所以时针与分针的夹角=4×30°=120°.
故答案为120.
18.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为 50 °.
解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+20°=50°,
故答案为:50
三、计算题(本大题共3小题,共18分)
19.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
解:(1)∵OA平分∠EOC,
∴∠AOC=∠EOC=×70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC=∠EOC=×72°=36°,
∴∠BOD=∠AOC=36°.
20.如图,直线AB、CD相交于点O,射线OM,ON分别平分∠AOC,∠AOD,求∠MON的度数.
【解答】证明:∵射线OM,ON分别平分∠AOC,∠AOD,
∴∠AOM=∠AOC,∠AON=∠AOD.
∴∠AOM+∠AON=(∠AOC+∠AOD),
即∠MON=∠COD.
∵∠COD=180°,
∴∠MON=∠COD=×180°=90°.
∴OM⊥ON.
21.(1)①如图1,已知AB∥CD,∠ABC=60°,根据 两直线平行,内错角相等 可得∠BCD= 60 °;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM= 30 °;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN= 60 °.
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
解:(1)①两直线平行,内错角相等;60;
②30;
③60.
(2)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,
∴∠BCN=140°÷2=70°.
∵CN⊥CM,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
四、解答题(本大题共4小题,共28分)
22.如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.
解:∵BE⊥AC,
∴∠BEC=90°,
∵DF∥BE,
∴∠BEC=∠DFC=90°,
∵∠C=64°,
∴∠FDC=180°﹣(∠DFC+∠C)
=180°﹣(90°+64°)
=26°,
∵∠ABC=36°,∠C=64°,
∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣36°﹣64°=80°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=×80°=40°,
∴∠AHB=∠DAC+∠BEA
=40°+90°
=130°.
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠EAD、∠DAC、∠C的度数.
解:∵AD∥BC,∠B=30°,
∴∠EAD=∠B=30°,
∵AD是∠EAC的平分线,
∴∠DAC=∠EAD=30°,
又∵AD∥BC,
∴∠C=∠DAC=30°.
24.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
解:如图,∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、
AC被直线BC所截形成的同位角.
25.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
【解答】证明:过E作EF∥AB 交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
