华师大版九年级上册22.3.1 用一元二次方程解决简单的应用问题课件(15张PPT)
文档属性
| 名称 | 华师大版九年级上册22.3.1 用一元二次方程解决简单的应用问题课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览





文档简介
用一元二次方程解决
简单的应用问题
列方程解应用题的一般步骤:
(1)
(2)
(3)
(4)
(5)
分析题意,设未知数
找出等量关系,列方程
解方程
看方程的解是否符合题意
答数
解一元二次方程有哪些方法:
直接开平方法、配方法、公式法、因式分解法.
情景导入
解方程:(1)(20-x)(30-x)=200;
(2)100(1+x)2=121.
自学互研
知识模块一 简单的几何图形问题
(一)自主探究
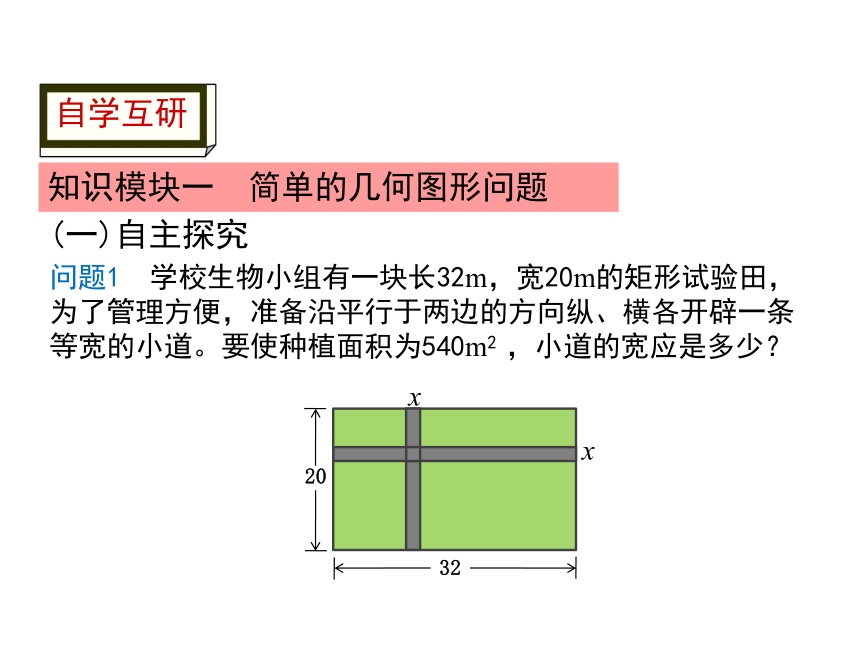
问题1 学校生物小组有一块长32m,宽20m的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道。要使种植面积为540m2 ,小道的宽应是多少?
x
20
x
32
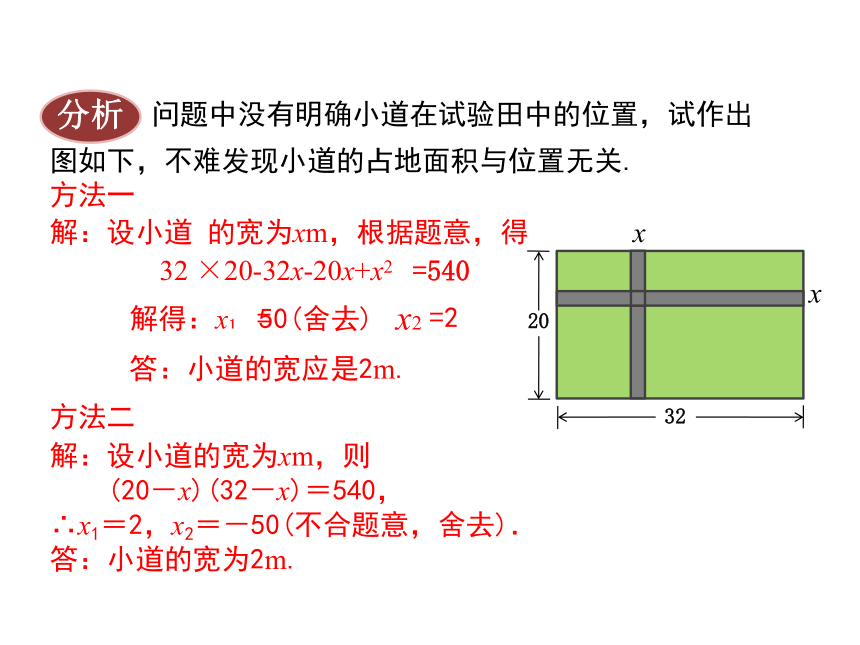
分析
问题中没有明确小道在试验田中的位置,试作出
图如下,不难发现小道的占地面积与位置无关.
解:设小道 的宽为xm,根据题意,得
32 ×20-32x-20x+x2
=540
解得:x?=
50(舍去)
=2
答:小道的宽应是2m.
x
20
x
32
解:设小道的宽为xm,则
(20-x)(32-x)=540,
∴x1=2,x2=-50(不合题意,舍去).
答:小道的宽为2m.
方法一
方法二
试一试 如果设想把小道平移到两边(如图),小道所占面积是 否保持不变?在这样的设想下,所列方程是否符合题目要求?处理问题是否方便些?
x
20
x
32
(二)合作探究
归纳:一元二次方程解应用题的一般步骤
(1)审题,分析题意,找出已知量和未知量,弄清它们之间的数量关系;
(2)设未知数,一般采取直接设法,有的要间接设;
(3)寻找数量关系,列出方程,要注意方程两边的数量相等,方程两边的代数式的单位相同;
(4)选择合适的方法解方程;
(5)检验.因为一元二次方程的解有可能不符合题意,如:线段的长度不能为负数等,因此,解出方程的根后,一定要进行检验.
问题2 某药品经过再次降价,每瓶零售价由56
若每次降价的百分率为x,则第一次降价后的零售价为原来的 倍,即56 倍,第二次降价后的零售价为56 元的 倍。
知识模块二 百分率问题
范例
元降为31.5元。已知两次降低的百分率相同。求每次降价的百分率。
分析
(一)自主探究
解:设每次降价的百分率为x,根据题意,得
56(1-x)2=31.5,
解这个方程,得
x1=0.25,x2=1.75.
因为降价的百分率不可能大于1,所以x2=1.75不符合题意.
经检验,x=0.25=25%符合本题要求.
答:每次降价的百分率为25%.
(二)合作探究
仿例
超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,求平均每月的增长率.
解:设平均每月增长x,则200(1+x)2=288,
∴x1=20%,x2=-2.2(不合题意,舍去).
答:平均每月增长20%.
展示提升
1.如图,某小区计划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少米?若设通道的宽为x米,则x应满足的方程为( )
A.(30-2x)(20-x)+2x2=468
B.20×30-30x-20·2x=468
C.20×30-20·2x+x2=468
D.(30-2x)(20-x)=468
D
2.劲威牌衬衣的价格经过连续两次降价后,由每件150元降至96元,求平均每次降价的百分率是多少,可列方程_________________.
150(1-x)2=96
3.为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
解:1
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是A,则它们的数量关系可表示为
其中增长取“+”,降低取“-”
课堂小结
这里要特别注意: 在列一元二次方程解应用题时,
由于所得的根一般有两个,所以要检验这两个根
是否符合实际问题的要求.
列一元二次方程解应用题的步骤与列一元一次方程解应用题的步骤类似,即审、设、列、解、检、答.
简单的应用问题
列方程解应用题的一般步骤:
(1)
(2)
(3)
(4)
(5)
分析题意,设未知数
找出等量关系,列方程
解方程
看方程的解是否符合题意
答数
解一元二次方程有哪些方法:
直接开平方法、配方法、公式法、因式分解法.
情景导入
解方程:(1)(20-x)(30-x)=200;
(2)100(1+x)2=121.
自学互研
知识模块一 简单的几何图形问题
(一)自主探究
问题1 学校生物小组有一块长32m,宽20m的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道。要使种植面积为540m2 ,小道的宽应是多少?
x
20
x
32
分析
问题中没有明确小道在试验田中的位置,试作出
图如下,不难发现小道的占地面积与位置无关.
解:设小道 的宽为xm,根据题意,得
32 ×20-32x-20x+x2
=540
解得:x?=
50(舍去)
=2
答:小道的宽应是2m.
x
20
x
32
解:设小道的宽为xm,则
(20-x)(32-x)=540,
∴x1=2,x2=-50(不合题意,舍去).
答:小道的宽为2m.
方法一
方法二
试一试 如果设想把小道平移到两边(如图),小道所占面积是 否保持不变?在这样的设想下,所列方程是否符合题目要求?处理问题是否方便些?
x
20
x
32
(二)合作探究
归纳:一元二次方程解应用题的一般步骤
(1)审题,分析题意,找出已知量和未知量,弄清它们之间的数量关系;
(2)设未知数,一般采取直接设法,有的要间接设;
(3)寻找数量关系,列出方程,要注意方程两边的数量相等,方程两边的代数式的单位相同;
(4)选择合适的方法解方程;
(5)检验.因为一元二次方程的解有可能不符合题意,如:线段的长度不能为负数等,因此,解出方程的根后,一定要进行检验.
问题2 某药品经过再次降价,每瓶零售价由56
若每次降价的百分率为x,则第一次降价后的零售价为原来的 倍,即56 倍,第二次降价后的零售价为56 元的 倍。
知识模块二 百分率问题
范例
元降为31.5元。已知两次降低的百分率相同。求每次降价的百分率。
分析
(一)自主探究
解:设每次降价的百分率为x,根据题意,得
56(1-x)2=31.5,
解这个方程,得
x1=0.25,x2=1.75.
因为降价的百分率不可能大于1,所以x2=1.75不符合题意.
经检验,x=0.25=25%符合本题要求.
答:每次降价的百分率为25%.
(二)合作探究
仿例
超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,求平均每月的增长率.
解:设平均每月增长x,则200(1+x)2=288,
∴x1=20%,x2=-2.2(不合题意,舍去).
答:平均每月增长20%.
展示提升
1.如图,某小区计划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少米?若设通道的宽为x米,则x应满足的方程为( )
A.(30-2x)(20-x)+2x2=468
B.20×30-30x-20·2x=468
C.20×30-20·2x+x2=468
D.(30-2x)(20-x)=468
D
2.劲威牌衬衣的价格经过连续两次降价后,由每件150元降至96元,求平均每次降价的百分率是多少,可列方程_________________.
150(1-x)2=96
3.为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
解:1
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是A,则它们的数量关系可表示为
其中增长取“+”,降低取“-”
课堂小结
这里要特别注意: 在列一元二次方程解应用题时,
由于所得的根一般有两个,所以要检验这两个根
是否符合实际问题的要求.
列一元二次方程解应用题的步骤与列一元一次方程解应用题的步骤类似,即审、设、列、解、检、答.
