23.3 5 课题 相似三角形的判定(一)课件(13张PPT)
文档属性
| 名称 | 23.3 5 课题 相似三角形的判定(一)课件(13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 20:54:33 | ||
图片预览





文档简介
相似三角形的判定(一)
情景导入
1.根据相似多边形的定义,你知道什么样的两个三角形相似吗?
2.还有判断两个三角形相似的方法吗?
3.思考:有没有其他简单的办法判断两个三角形相似?
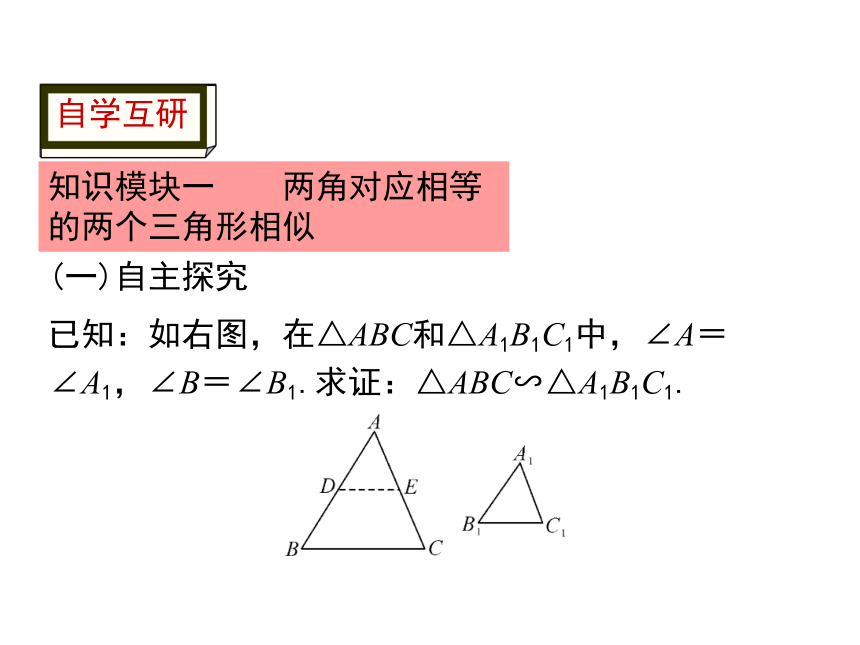
自学互研
知识模块一 两角对应相等的两个三角形相似
(一)自主探究
已知:如右图,在△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1.求证:△ABC∽△A1B1C1.
自学互研
知识模块一 两角对应相等的两个三角形相似
证明:在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,
则△ADE∽△ABC.
∵DE∥BC,∴∠ADE=∠B.
在△ADE与△A1B1C1中,
∵∠A=∠A1,∠ADE=∠B=∠B1,AD=A1B1,
∴△ADE≌△A1B1C1,
∴△ABC∽△A1B1C1.
(二)合作探究
问题:如果两个三角形仅有一个角对应相等,那么这两个三角形相似吗?
归纳:三角形相似的判定定理1:
两个角对应相等的两个三角形相似.
知识模块二 两角对应相等的两个三角形相似的应用
(一)自主探究
范例
如图,在Rt△ABC和Rt△A′B′C′中,∠C与∠C′都是直角,∠A=∠A′,求证△ABC∽△A′B′C′.
证明:∵∠C=∠C′=90°,
∠A=∠A′.
∴△ABC∽△A′B′C′
(两角分别相等的两个三角形相似).
如右图,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
范例
证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
又∵EF∥AB,
∴∠EFC=∠B,∴∠ADE=∠EFC,
∴△ADE∽△EFC
(两角分别相等的两个三角形相似).
范例
如图,已知在△ABC中,∠BAC=90°,BC的垂线交BC于D,交AC于E,交BA的延长线于F,
求证:BD·DC=DE·DF.
证明:∵∠BAC=90°,
∴∠B+∠C=90°,
∵FD⊥BC,
∴∠BDF=∠CDE=90°,
∠B+∠F=90°,
∴∠F=∠C,∴△BDF∽△EDC,
∴BD·DC=DE·DF
展示提升
1.下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个30°的内角
B.都含有一个45°的内角
C.都含有一个60°的内角
D.都含有一个80°的内角
C
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对 B.2对
3.如图,要使△ADB∽△ABC,还需增添的条件是________________________ (写一个即可).
C.3对 D.4对
C
∠C=∠ABD,不唯一
4.如图,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠1+∠2=90°.求证:△ABC∽△CDE.
证明:∵AB⊥BC,ED⊥CD,
∴∠B=∠D=90°,
∠1+∠A=90°.
∵∠1+∠2=90°,
∴∠A=∠2,
∴△ABC∽△CDE.
5.如图,△ACB是等腰直角三角形,点O为斜边AB的中点,∠EOF=45°.
(1)求证:△AOE∽△BFO;
(2)若AB=4,求AE·BF的值.
解:(1)提示:
证∠A=∠B, ∠AOE=∠BFO;
(2)AE·BF=OA2=4
相似三角形的识别方法有那些?
方法1:通过定义
方法3:通过两角对应相等。
方法2:平行于三角形一边的直线。
课堂小结
情景导入
1.根据相似多边形的定义,你知道什么样的两个三角形相似吗?
2.还有判断两个三角形相似的方法吗?
3.思考:有没有其他简单的办法判断两个三角形相似?
自学互研
知识模块一 两角对应相等的两个三角形相似
(一)自主探究
已知:如右图,在△ABC和△A1B1C1中,∠A=∠A1,∠B=∠B1.求证:△ABC∽△A1B1C1.
自学互研
知识模块一 两角对应相等的两个三角形相似
证明:在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,
则△ADE∽△ABC.
∵DE∥BC,∴∠ADE=∠B.
在△ADE与△A1B1C1中,
∵∠A=∠A1,∠ADE=∠B=∠B1,AD=A1B1,
∴△ADE≌△A1B1C1,
∴△ABC∽△A1B1C1.
(二)合作探究
问题:如果两个三角形仅有一个角对应相等,那么这两个三角形相似吗?
归纳:三角形相似的判定定理1:
两个角对应相等的两个三角形相似.
知识模块二 两角对应相等的两个三角形相似的应用
(一)自主探究
范例
如图,在Rt△ABC和Rt△A′B′C′中,∠C与∠C′都是直角,∠A=∠A′,求证△ABC∽△A′B′C′.
证明:∵∠C=∠C′=90°,
∠A=∠A′.
∴△ABC∽△A′B′C′
(两角分别相等的两个三角形相似).
如右图,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
范例
证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
又∵EF∥AB,
∴∠EFC=∠B,∴∠ADE=∠EFC,
∴△ADE∽△EFC
(两角分别相等的两个三角形相似).
范例
如图,已知在△ABC中,∠BAC=90°,BC的垂线交BC于D,交AC于E,交BA的延长线于F,
求证:BD·DC=DE·DF.
证明:∵∠BAC=90°,
∴∠B+∠C=90°,
∵FD⊥BC,
∴∠BDF=∠CDE=90°,
∠B+∠F=90°,
∴∠F=∠C,∴△BDF∽△EDC,
∴BD·DC=DE·DF
展示提升
1.下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个30°的内角
B.都含有一个45°的内角
C.都含有一个60°的内角
D.都含有一个80°的内角
C
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对 B.2对
3.如图,要使△ADB∽△ABC,还需增添的条件是________________________ (写一个即可).
C.3对 D.4对
C
∠C=∠ABD,不唯一
4.如图,点B、C、D在一条直线上,AB⊥BC,ED⊥CD,∠1+∠2=90°.求证:△ABC∽△CDE.
证明:∵AB⊥BC,ED⊥CD,
∴∠B=∠D=90°,
∠1+∠A=90°.
∵∠1+∠2=90°,
∴∠A=∠2,
∴△ABC∽△CDE.
5.如图,△ACB是等腰直角三角形,点O为斜边AB的中点,∠EOF=45°.
(1)求证:△AOE∽△BFO;
(2)若AB=4,求AE·BF的值.
解:(1)提示:
证∠A=∠B, ∠AOE=∠BFO;
(2)AE·BF=OA2=4
相似三角形的识别方法有那些?
方法1:通过定义
方法3:通过两角对应相等。
方法2:平行于三角形一边的直线。
课堂小结
