23.4 9课题 中位线课件(13张PPT)
文档属性
| 名称 | 23.4 9课题 中位线课件(13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览


文档简介
23.4 中位线
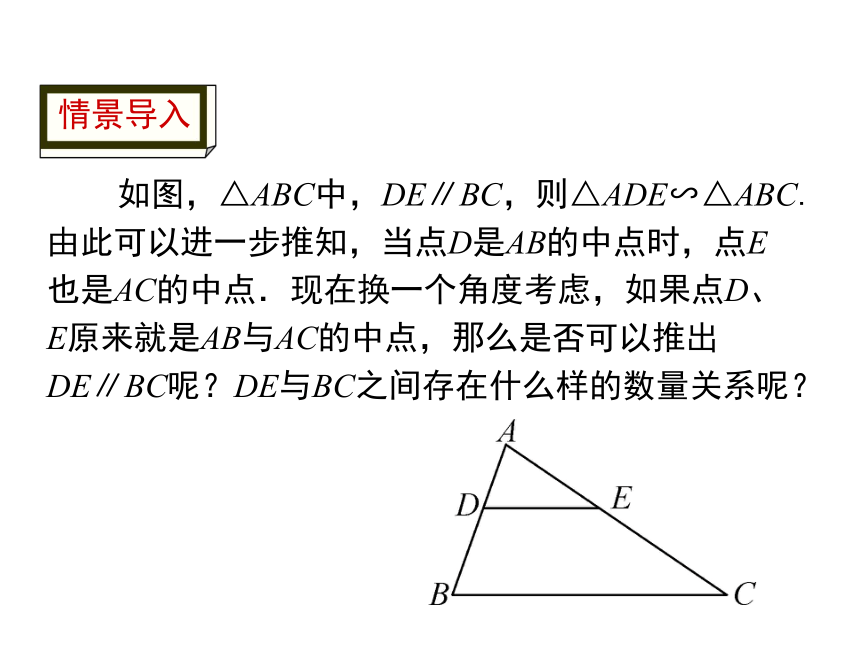
情景导入
如图,△ABC中,DE∥BC,则△ADE∽△ABC.由此可以进一步推知,当点D是AB的中点时,点E也是AC的中点.现在换一个角度考虑,如果点D、E原来就是AB与AC的中点,那么是否可以推出DE∥BC呢?DE与BC之间存在什么样的数量关系呢?
自学互研
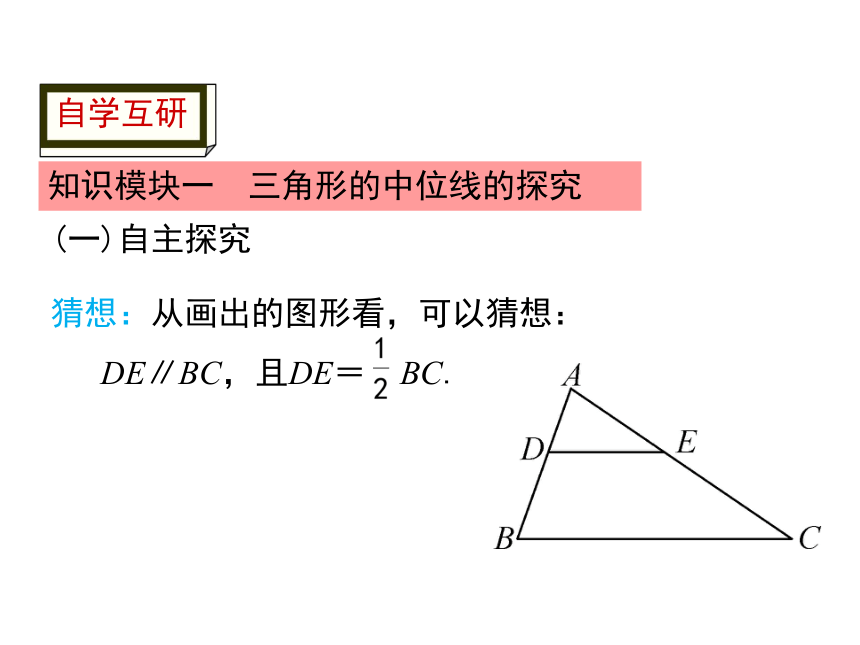
知识模块一 三角形的中位线的探究
(一)自主探究
猜想:从画出的图形看,可以猜想:
DE∥BC,且DE= BC.
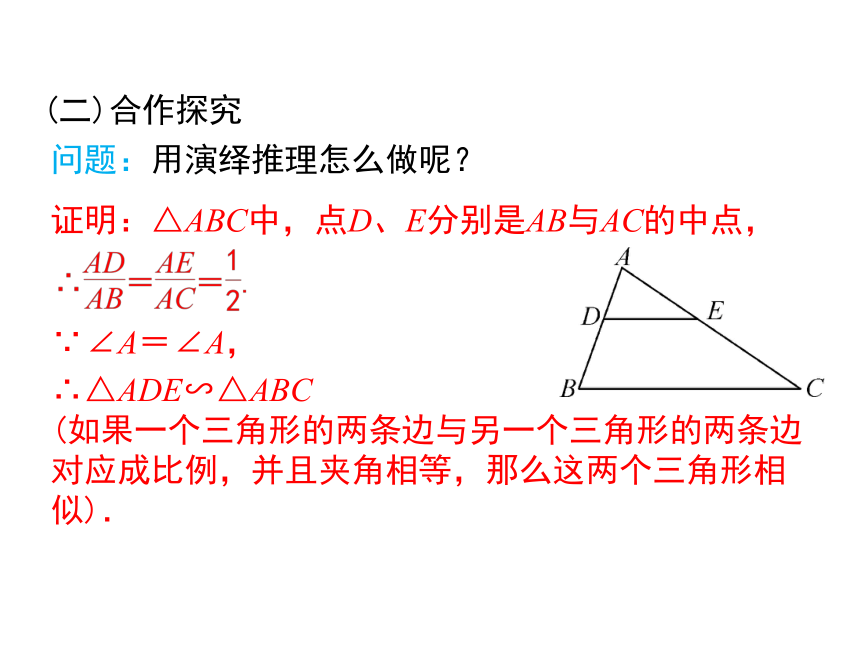
(二)合作探究
问题:用演绎推理怎么做呢?
证明:△ABC中,点D、E分别是AB与AC的中点,
∴△ADE∽△ABC
(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似).
∵∠A=∠A,
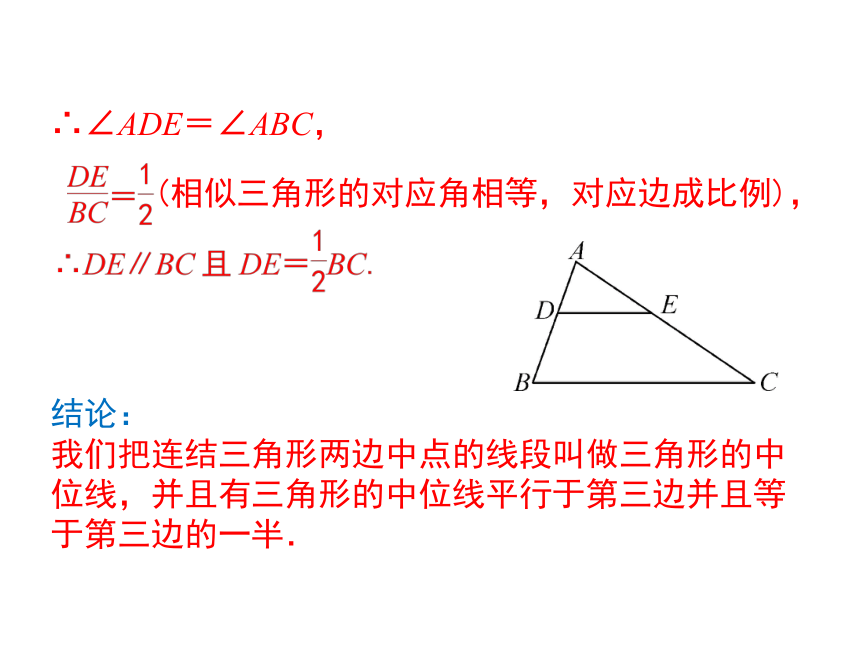
结论:
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有三角形的中位线平行于第三边并且等于第三边的一半.
(相似三角形的对应角相等,对应边成比例),
∴∠ADE=∠ABC,
知识模块二 三角形中位线的简单应用
范例
求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.求证:AE、DF互相平分.
证明:连结DE、EF.
因为AD=DB,BE=EC,
所以DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半),
同理EF∥AB,
所以四边形ADEF是平行四边形,因此AE、DF互相平分(平行四边形的对角线互相平分).
仿例
如图,△ABC中,D、E分别是边BC、AB的
中点,AD、CE相交于G.
证明:连结ED,
∵D、E分别是边BC、AB的中点,
∴DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴△ACG∽△DEG,
拓展
如果在如图中,取AC的中点F,假设BF与AD
交于G′,如图,那么我们同理有
所以有
即两图中的点G与G′是重合的.
结论:三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的三分之一.
展示提升
1.如图,D、E、F三点分别为△ABC三边的中点,则下列说法中不正确的是( )
D.DF=EF
B.S△ABF=S△AFC
A.△ADE∽△ABC
D
2.如图,在△ABC中 ,AB=4,AC=6,AD平分∠BAC,BD⊥AD于D,E是BC的中点,则DE=____.
3.在Rt△ABC中,∠ABC=90°,AC=6,点P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=____.
1
1
4.D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连结OB、OC,点G、F分别是OB、OC的中点,顺次连结点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
解:∵D、E、G、F分别是AB、AC、OB、OC的中点,
∴DE∥BC,GF∥BC,
∴DE∥GF,DE=GF,
∴四边形DGFE是平行四边形.
DE= BC,GF= BC,
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由).
解:OA=BC
课堂小结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.
3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.
情景导入
如图,△ABC中,DE∥BC,则△ADE∽△ABC.由此可以进一步推知,当点D是AB的中点时,点E也是AC的中点.现在换一个角度考虑,如果点D、E原来就是AB与AC的中点,那么是否可以推出DE∥BC呢?DE与BC之间存在什么样的数量关系呢?
自学互研
知识模块一 三角形的中位线的探究
(一)自主探究
猜想:从画出的图形看,可以猜想:
DE∥BC,且DE= BC.
(二)合作探究
问题:用演绎推理怎么做呢?
证明:△ABC中,点D、E分别是AB与AC的中点,
∴△ADE∽△ABC
(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似).
∵∠A=∠A,
结论:
我们把连结三角形两边中点的线段叫做三角形的中位线,并且有三角形的中位线平行于第三边并且等于第三边的一半.
(相似三角形的对应角相等,对应边成比例),
∴∠ADE=∠ABC,
知识模块二 三角形中位线的简单应用
范例
求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.求证:AE、DF互相平分.
证明:连结DE、EF.
因为AD=DB,BE=EC,
所以DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半),
同理EF∥AB,
所以四边形ADEF是平行四边形,因此AE、DF互相平分(平行四边形的对角线互相平分).
仿例
如图,△ABC中,D、E分别是边BC、AB的
中点,AD、CE相交于G.
证明:连结ED,
∵D、E分别是边BC、AB的中点,
∴DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴△ACG∽△DEG,
拓展
如果在如图中,取AC的中点F,假设BF与AD
交于G′,如图,那么我们同理有
所以有
即两图中的点G与G′是重合的.
结论:三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线的长是对应中线长的三分之一.
展示提升
1.如图,D、E、F三点分别为△ABC三边的中点,则下列说法中不正确的是( )
D.DF=EF
B.S△ABF=S△AFC
A.△ADE∽△ABC
D
2.如图,在△ABC中 ,AB=4,AC=6,AD平分∠BAC,BD⊥AD于D,E是BC的中点,则DE=____.
3.在Rt△ABC中,∠ABC=90°,AC=6,点P、Q分别为AC、BC的中点,AQ、BP相交于点O,则OP=____.
1
1
4.D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连结OB、OC,点G、F分别是OB、OC的中点,顺次连结点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
解:∵D、E、G、F分别是AB、AC、OB、OC的中点,
∴DE∥BC,GF∥BC,
∴DE∥GF,DE=GF,
∴四边形DGFE是平行四边形.
DE= BC,GF= BC,
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由).
解:OA=BC
课堂小结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.
3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.
