23.3 8 课题 相似三角形的应用课件(15张PPT)
文档属性
| 名称 | 23.3 8 课题 相似三角形的应用课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览




文档简介
相似三角形的应用
情景导入
1.识别两个三角形相似的方法有哪些?
2.相似三角形有哪些性质?
自学互研
知识模块一 相似三角形的应用一
(一)自主探究
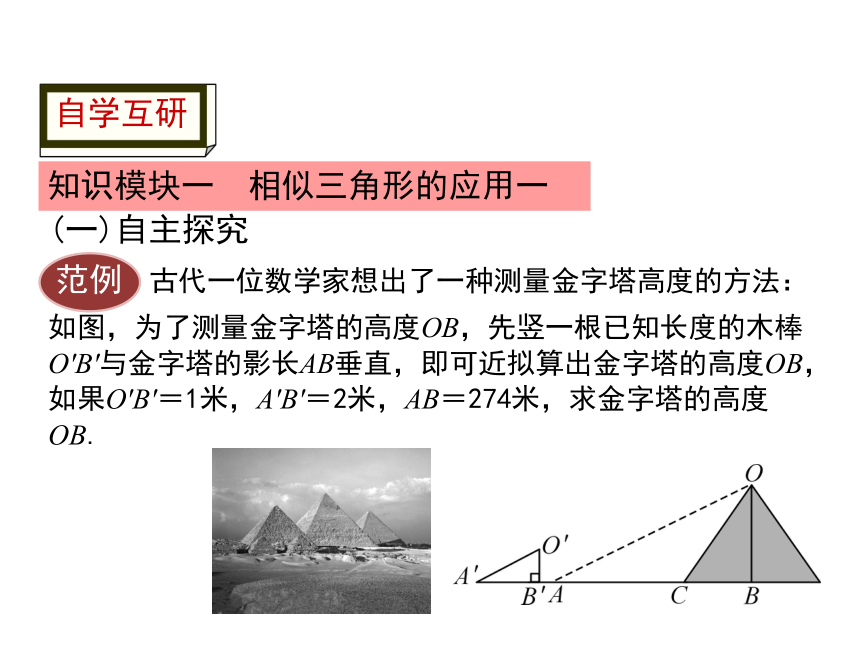
范例
古代一位数学家想出了一种测量金字塔高度的方法:
如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′与金字塔的影长AB垂直,即可近拟算出金字塔的高度OB,如果O′B′=1米,A′B′=2米,AB=274米,求金字塔的高度OB.
解:∵太阳光线是平行光线,
∴∠OAB=∠O′A′B′.
∵∠ABO=∠A′B′O′=90°,
答:金字塔的高度OB为137米.
∴△OAB∽△O′A′B′
(两角分别相等的两个三角形相似).
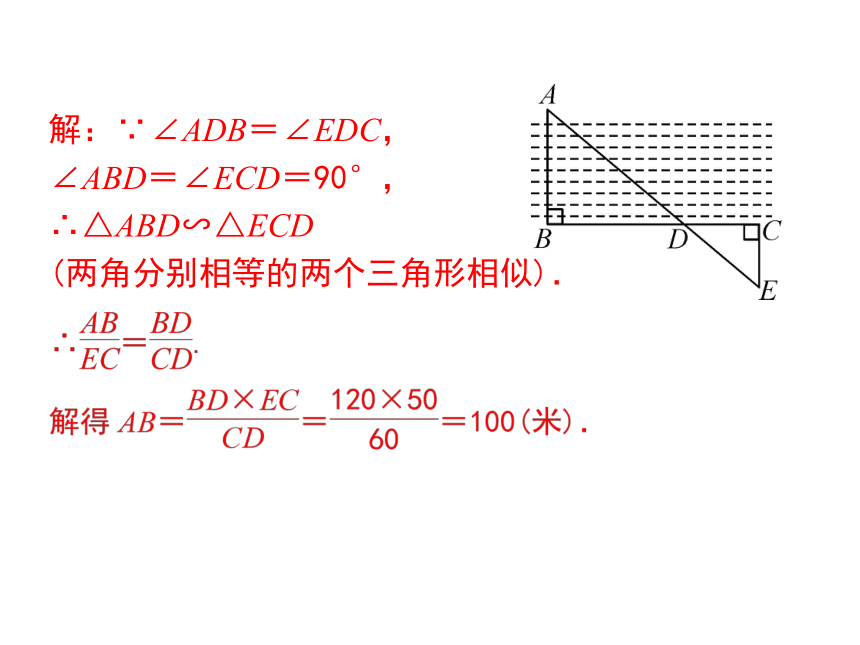
范例
如右图,为了估算河的宽度,我们可以在河
对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选定点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
解:∵∠ADB=∠EDC,
∠ABD=∠ECD=90°,
∴△ABD∽△ECD
(两角分别相等的两个三角形相似).
知识模块二 相似三角形的应用二
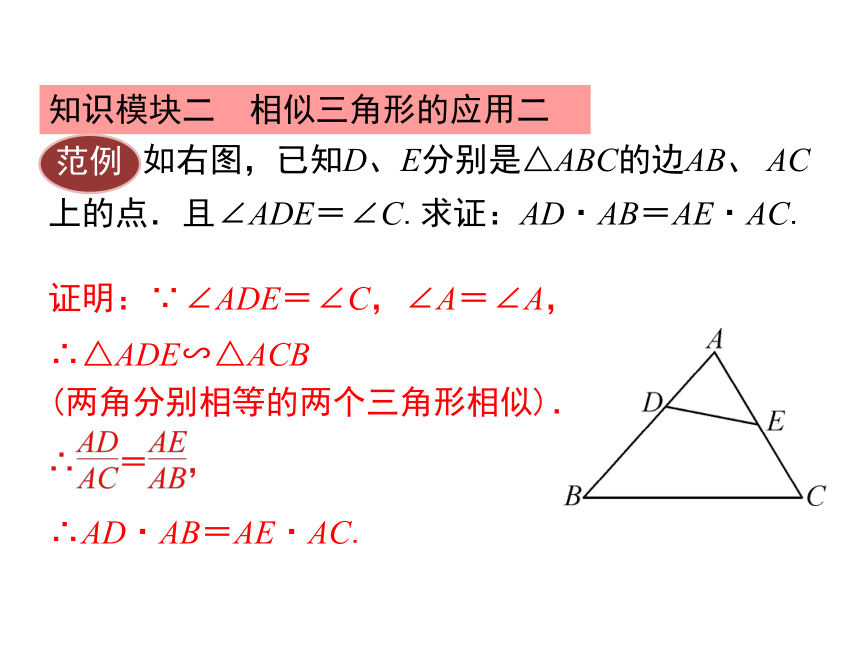
范例
如右图,已知D、E分别是△ABC的边AB、 AC
上的点.且∠ADE=∠C.求证:AD·AB=AE·AC.
证明:∵∠ADE=∠C,∠A=∠A,
∴AD·AB=AE·AC.
∴△ADE∽△ACB
(两角分别相等的两个三角形相似).
仿例
如图,AE= EC,AD= DB,测得DE=20米,
求池塘宽BC是多少米?
解:∵ AE= EC,AD= DB, ∠A=∠A,
∴△ADE∽△ABC,
∵DE=20米,
∴BC=60米.
答:池塘宽BC为60米.
仿例
小明在打网球时,使球恰好能过网,而且落在
离网5米的位置上,已知如图,求球拍击球的高度h?(设网球作直线运动)
解:∵DE⊥AB,CB⊥AB,
∴DE∥BC,
∵DE=0.8,AD=5,AB=15,
答:球拍击球高度为2.4米.
∴BC=2.4米.
展示提升
1.如图,在△ABC中,DE∥BC,
则下列结论
中正确的是( )
C
2.已知△ABC∽△A′B′C′且S△ABC∶S△A′B′C′=16∶9,若AB=2,则A′B′=____.
3.如图,矩形ABCD,DE⊥AC交AC于F,交BC于E,
若EF∶DF=1∶2,则 ____
1.5
4.如图,四边形DEFG是Rt△ABC的内接正方形,若CF=8,
求BE的长.
解:BE=4.
5.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯CD的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
解:CD≈6.1m
课堂小结
1. 相似三角形的应用主要有两个方面:
(1)测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺测量)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2)测距
2. 解相似三角形实际问题的一般步骤:
(1)审题;
(2)构建图形;
(3)利用相似解决问题.
情景导入
1.识别两个三角形相似的方法有哪些?
2.相似三角形有哪些性质?
自学互研
知识模块一 相似三角形的应用一
(一)自主探究
范例
古代一位数学家想出了一种测量金字塔高度的方法:
如图,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′与金字塔的影长AB垂直,即可近拟算出金字塔的高度OB,如果O′B′=1米,A′B′=2米,AB=274米,求金字塔的高度OB.
解:∵太阳光线是平行光线,
∴∠OAB=∠O′A′B′.
∵∠ABO=∠A′B′O′=90°,
答:金字塔的高度OB为137米.
∴△OAB∽△O′A′B′
(两角分别相等的两个三角形相似).
范例
如右图,为了估算河的宽度,我们可以在河
对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选定点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
解:∵∠ADB=∠EDC,
∠ABD=∠ECD=90°,
∴△ABD∽△ECD
(两角分别相等的两个三角形相似).
知识模块二 相似三角形的应用二
范例
如右图,已知D、E分别是△ABC的边AB、 AC
上的点.且∠ADE=∠C.求证:AD·AB=AE·AC.
证明:∵∠ADE=∠C,∠A=∠A,
∴AD·AB=AE·AC.
∴△ADE∽△ACB
(两角分别相等的两个三角形相似).
仿例
如图,AE= EC,AD= DB,测得DE=20米,
求池塘宽BC是多少米?
解:∵ AE= EC,AD= DB, ∠A=∠A,
∴△ADE∽△ABC,
∵DE=20米,
∴BC=60米.
答:池塘宽BC为60米.
仿例
小明在打网球时,使球恰好能过网,而且落在
离网5米的位置上,已知如图,求球拍击球的高度h?(设网球作直线运动)
解:∵DE⊥AB,CB⊥AB,
∴DE∥BC,
∵DE=0.8,AD=5,AB=15,
答:球拍击球高度为2.4米.
∴BC=2.4米.
展示提升
1.如图,在△ABC中,DE∥BC,
则下列结论
中正确的是( )
C
2.已知△ABC∽△A′B′C′且S△ABC∶S△A′B′C′=16∶9,若AB=2,则A′B′=____.
3.如图,矩形ABCD,DE⊥AC交AC于F,交BC于E,
若EF∶DF=1∶2,则 ____
1.5
4.如图,四边形DEFG是Rt△ABC的内接正方形,若CF=8,
求BE的长.
解:BE=4.
5.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯CD的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
解:CD≈6.1m
课堂小结
1. 相似三角形的应用主要有两个方面:
(1)测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺测量)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2)测距
2. 解相似三角形实际问题的一般步骤:
(1)审题;
(2)构建图形;
(3)利用相似解决问题.
