23.3 6 课题 相似三角形的判定(二)课件(13张PPT)
文档属性
| 名称 | 23.3 6 课题 相似三角形的判定(二)课件(13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览



文档简介
相似三角形的判定(二)
判断两个三角形相似,你有哪些方法?
方法1:通过定义(不常用)
方法2:通过平行线。
方法3:两角对应相等。
情景导入
自学互研
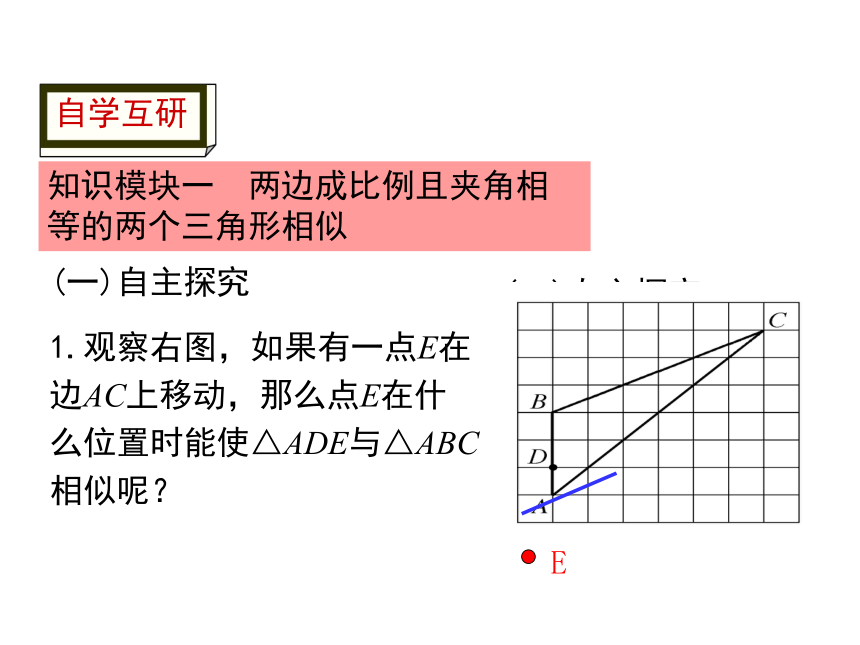
知识模块一 两边成比例且夹角相等的两个三角形相似
(一)自主探究
1.观察右图,如果有一点E在边AC上移动,那么点E在什么位置时能使△ADE与△ABC相似呢?
E
(一)自主探究
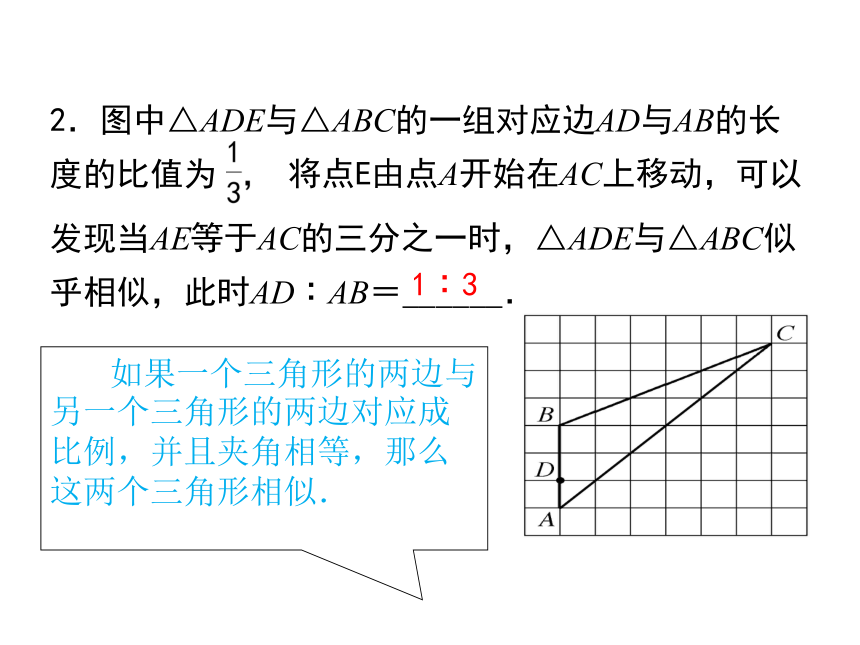
如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.
2.图中△ADE与△ABC的一组对应边AD与AB的长度的比值为
将点E由点A开始在AC上移动,可以
发现当AE等于AC的三分之一时,△ADE与△ABC似乎相似,此时AD∶AB=______.
1∶3
(二)合作探究
已知:如图,在△ABC和△A1B1C1中,∠A=∠A1,
求证:△ABC∽△A1B1C1.
证明:在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,则△ADE∽△ABC,
AD=A1B1,
∴AE=A1C1,在△ADE和△A1B1C1中,
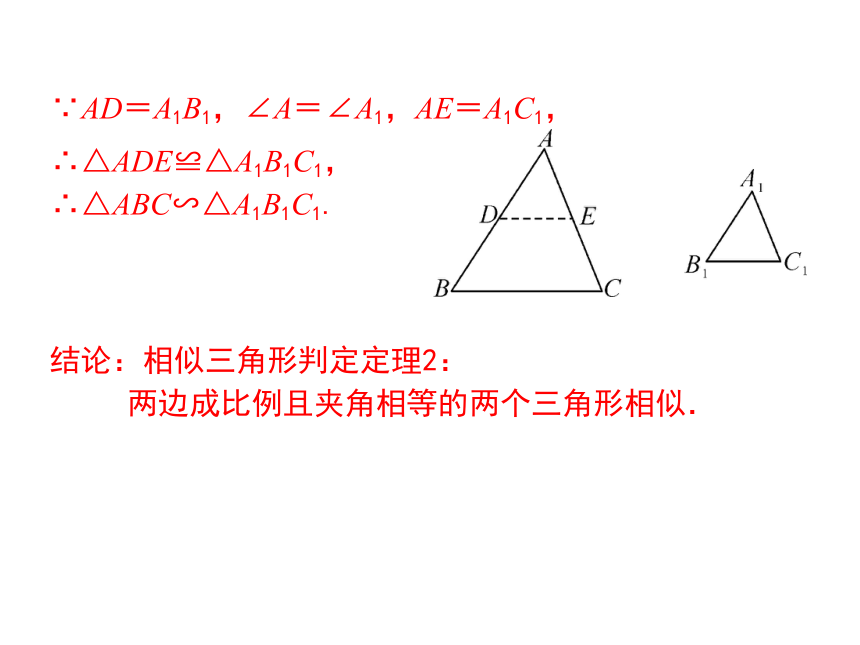
结论:相似三角形判定定理2:
两边成比例且夹角相等的两个三角形相似.
∵AD=A1B1,∠A=∠A1,AE=A1C1,
∴△ADE≌△A1B1C1,∴△ABC∽△A1B1C1.
范例
证明:如图中的△AEB和△FEC相似.
证明:
又∵∠AEB=∠FEC,
∴△AEB∽△FEC
(两边成比例且夹角相等的两个三角形相似)
知识模块二 三边对应成比例的两个三角形相似
(一)自主探究
探索:三边对应相等的两个三角形全等,那么三边对应成比例的两个三角形相似吗?
在如图所示的方格图中任画一个三角形,再画出第二个三角形,使它的三边长都是原来三角形三边长的相同倍数,画完之后,用量角器度量并比较两个三角形对应角的大小,你得出了什么结论?
结论:相似三角形的判定定理3:
三边对应成比例的两个三角形相似.
(二)合作探究
范例
在△ABC和△A′B′C′中,AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm,试证明△ABC与△A′B′C′相似.
∴△ABC∽△A′B′C′
(三边成比例的两个三角形相似).
展示提升
1.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B
C
2.如图,在△ABC中,D是边AC上一点,连结BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD·AC;③AD·BC=AB·BD;④AB·BC=AC·BD.其中单独能够判断△ABD∽△ACB的个数是( )
C.3个 D.4个
A.1个 B.2个
B
3.在△ABC中,∠C=90°,CD⊥AB于D,如果AD=9,BD=16,那么CD=____,AC=____.
4.如图,在△ABC中,AB=4,AC=8,点P从B点出发沿BA方向以每秒1个单位移动;点Q从A出发沿AC方向以每秒2个单位移动,当它们到达A、C后停止运动,试问经过几秒后,△ABC与△APQ相似?请说明理由.
12
15
课堂小结
简单地说:三边对应成比例,两三角形相似.
相似三角形的判定定理:
相似三角形的判定定理1:两角分别相等的两个三角形相似.
相似三角形的判定定理2: 如果两个三角形两边对应成比例,两条对应边的夹角相等,那么两个三角形相似.
注意:对应相等的角一定要是两条对应边的夹角.
相似三角形的判定定理3: 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
判断两个三角形相似,你有哪些方法?
方法1:通过定义(不常用)
方法2:通过平行线。
方法3:两角对应相等。
情景导入
自学互研
知识模块一 两边成比例且夹角相等的两个三角形相似
(一)自主探究
1.观察右图,如果有一点E在边AC上移动,那么点E在什么位置时能使△ADE与△ABC相似呢?
E
(一)自主探究
如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.
2.图中△ADE与△ABC的一组对应边AD与AB的长度的比值为
将点E由点A开始在AC上移动,可以
发现当AE等于AC的三分之一时,△ADE与△ABC似乎相似,此时AD∶AB=______.
1∶3
(二)合作探究
已知:如图,在△ABC和△A1B1C1中,∠A=∠A1,
求证:△ABC∽△A1B1C1.
证明:在边AB或它的延长线上截取AD=A1B1,
过点D作BC的平行线交AC于点E,则△ADE∽△ABC,
AD=A1B1,
∴AE=A1C1,在△ADE和△A1B1C1中,
结论:相似三角形判定定理2:
两边成比例且夹角相等的两个三角形相似.
∵AD=A1B1,∠A=∠A1,AE=A1C1,
∴△ADE≌△A1B1C1,∴△ABC∽△A1B1C1.
范例
证明:如图中的△AEB和△FEC相似.
证明:
又∵∠AEB=∠FEC,
∴△AEB∽△FEC
(两边成比例且夹角相等的两个三角形相似)
知识模块二 三边对应成比例的两个三角形相似
(一)自主探究
探索:三边对应相等的两个三角形全等,那么三边对应成比例的两个三角形相似吗?
在如图所示的方格图中任画一个三角形,再画出第二个三角形,使它的三边长都是原来三角形三边长的相同倍数,画完之后,用量角器度量并比较两个三角形对应角的大小,你得出了什么结论?
结论:相似三角形的判定定理3:
三边对应成比例的两个三角形相似.
(二)合作探究
范例
在△ABC和△A′B′C′中,AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm,试证明△ABC与△A′B′C′相似.
∴△ABC∽△A′B′C′
(三边成比例的两个三角形相似).
展示提升
1.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B
C
2.如图,在△ABC中,D是边AC上一点,连结BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD·AC;③AD·BC=AB·BD;④AB·BC=AC·BD.其中单独能够判断△ABD∽△ACB的个数是( )
C.3个 D.4个
A.1个 B.2个
B
3.在△ABC中,∠C=90°,CD⊥AB于D,如果AD=9,BD=16,那么CD=____,AC=____.
4.如图,在△ABC中,AB=4,AC=8,点P从B点出发沿BA方向以每秒1个单位移动;点Q从A出发沿AC方向以每秒2个单位移动,当它们到达A、C后停止运动,试问经过几秒后,△ABC与△APQ相似?请说明理由.
12
15
课堂小结
简单地说:三边对应成比例,两三角形相似.
相似三角形的判定定理:
相似三角形的判定定理1:两角分别相等的两个三角形相似.
相似三角形的判定定理2: 如果两个三角形两边对应成比例,两条对应边的夹角相等,那么两个三角形相似.
注意:对应相等的角一定要是两条对应边的夹角.
相似三角形的判定定理3: 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
