23.6 12 课题 图形的变换与坐标课件(13张PPT)
文档属性
| 名称 | 23.6 12 课题 图形的变换与坐标课件(13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 21:09:54 | ||
图片预览




文档简介
23.6.2 图形的变换与坐标
情景导入
1.平移的特征是什么?
2.轴对称图形的特征是什么?
3.相似图形的特征是什么?
自学互研
知识模块一 图形的平移
(一)自主探究
范例
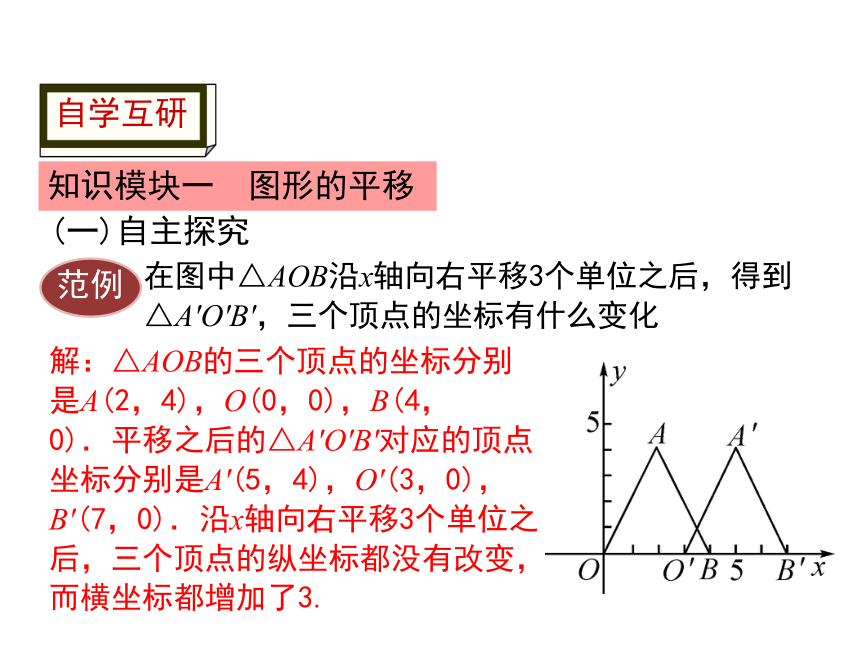
在图中△AOB沿x轴向右平移3个单位之后,得到△A′O′B′,三个顶点的坐标有什么变化
解:△AOB的三个顶点的坐标分别是A(2,4),O(0,0),B(4,0).平移之后的△A′O′B′对应的顶点坐标分别是A′(5,4),O′(3,0),B′(7,0).沿x轴向右平移3个单位之后,三个顶点的纵坐标都没有改变,而横坐标都增加了3.
范例
如图,△ABC的三个顶点的坐标分别为
(-3,4)、(-4,3)和(-1,3).将△ABC沿y轴向下平移3个单位得到△A′B′C′,然后再将△A′B′C′沿x轴向右平移4个单位得到△A″B″C″.试写出现在三个顶点的坐标,看看发生了什么变化.
解:△ABC的三个顶点的坐标分别是A(-3,4),B(-4,3),C(-1,3),沿y轴向下平移3个单位之后的△A′B′C′对应的顶点坐标分别是A′(-3,1),B′(-4,0),C′(-1,0).沿x轴向右平移4个单位之后的△A″B″C″对应的顶点坐标分别是A″(1,1),B″(0,0),C″(3,0).经过两次平移后,三角形三个顶点的横坐标都增加了4,纵坐标都减少了3.我们还可以把这两次平移看作是△ABC沿BB″方向平移一次,得到△A″B″C″.
知识模块二 轴对称
O
y
x
A
B
A′
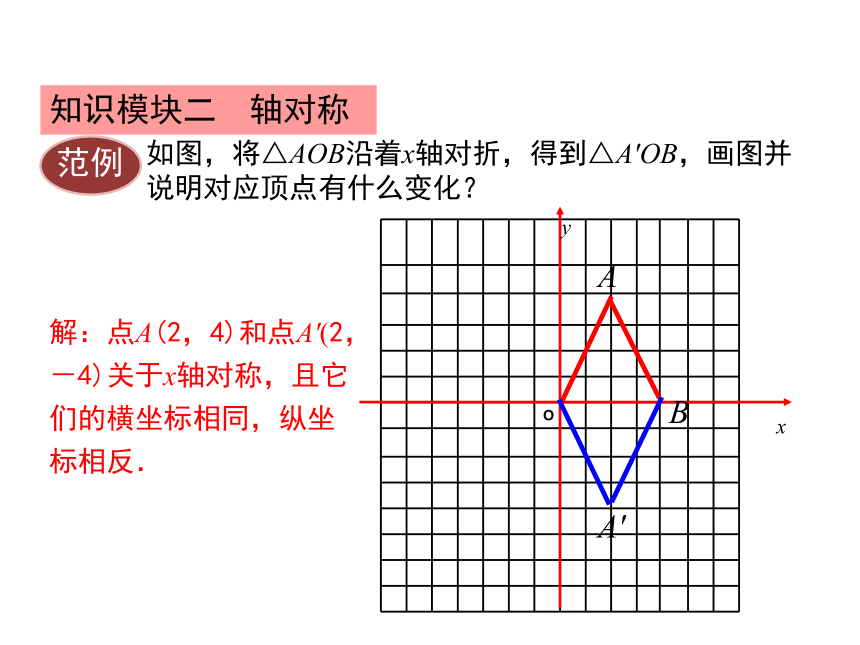
如图,将△AOB沿着x轴对折,得到△A′OB,画图并说明对应顶点有什么变化?
范例
解:点A(2,4)和点A′(2,-4)关于x轴对称,且它们的横坐标相同,纵坐标相反.
仿例
请在右图中的平面直角坐标系中画一个平行
四边形,写出它的四个顶点的坐标,然后画出这个平行四边形关于y轴的对称图形,写出对称图形四个顶点的坐标,观察对应顶点的坐标有什么变化.
知识模块三 相似
范例
如图,将△AOB缩小后得到△COD,你能求
出它们的相似比吗?
探索:如图,已知矩形ABCD四个顶点的坐标分别是A(0,0)、B(3,0)、C(3,2)、D(0,2),将这四个顶点坐标同时扩大到原来的2倍后得到一组新坐标,画出新坐标对应的点所确定的图形,看看新的图形和原图形之间有什么关系.
概括:我们看到,当一个几何图形经过某种运动改变位置后,图形上各点的坐标也发生了相应的变化,这些变化可以归纳成下表(请补充完整表格中的内容).
图形变换
关于x轴对称
关于y轴对称
关于原点对称
沿x轴向右平移a个单位
沿y轴向上平移b个单位
图形以原点为位似中心缩放4倍
运动前
点的坐标
(x,y)
运动后
点的坐标
(x,-y)
(x+a,y)
反过来,以某种方式同时改变一个几何图形上各点的坐标,也会使该图形产生相应的变换,从而改变它的位置或大小.
展示提升
1.已知点A(a,3)和B(4,b)关于y轴对称,则(a+b)2017的值为( )
A.-1 B.1 C.72017 D.-72017
A
2.平面直角坐标系中,A(-2,1),B(1,-2),将线段AB平移得到A′B′,且A′(1,3),则B′的坐标为________ .
3.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为
B′(4,0)
则A′的坐标为:__________________.
(4,6)或(-4,-6)
课堂小结
图形左右移动时,对应的横坐标左减右加,纵坐标不变.
图形上下移动时,对应的横坐标不变,纵坐标上加下减.
对应点关于x轴对称.即对应点的横坐标相等、纵坐标互为相反数.
对应点关于 y 轴对称.即对应点的横坐标互为相反数、纵坐标相等.
规律:对应点关于原点对称.即对应点的横坐标和纵坐标都互为相反数.
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
情景导入
1.平移的特征是什么?
2.轴对称图形的特征是什么?
3.相似图形的特征是什么?
自学互研
知识模块一 图形的平移
(一)自主探究
范例
在图中△AOB沿x轴向右平移3个单位之后,得到△A′O′B′,三个顶点的坐标有什么变化
解:△AOB的三个顶点的坐标分别是A(2,4),O(0,0),B(4,0).平移之后的△A′O′B′对应的顶点坐标分别是A′(5,4),O′(3,0),B′(7,0).沿x轴向右平移3个单位之后,三个顶点的纵坐标都没有改变,而横坐标都增加了3.
范例
如图,△ABC的三个顶点的坐标分别为
(-3,4)、(-4,3)和(-1,3).将△ABC沿y轴向下平移3个单位得到△A′B′C′,然后再将△A′B′C′沿x轴向右平移4个单位得到△A″B″C″.试写出现在三个顶点的坐标,看看发生了什么变化.
解:△ABC的三个顶点的坐标分别是A(-3,4),B(-4,3),C(-1,3),沿y轴向下平移3个单位之后的△A′B′C′对应的顶点坐标分别是A′(-3,1),B′(-4,0),C′(-1,0).沿x轴向右平移4个单位之后的△A″B″C″对应的顶点坐标分别是A″(1,1),B″(0,0),C″(3,0).经过两次平移后,三角形三个顶点的横坐标都增加了4,纵坐标都减少了3.我们还可以把这两次平移看作是△ABC沿BB″方向平移一次,得到△A″B″C″.
知识模块二 轴对称
O
y
x
A
B
A′
如图,将△AOB沿着x轴对折,得到△A′OB,画图并说明对应顶点有什么变化?
范例
解:点A(2,4)和点A′(2,-4)关于x轴对称,且它们的横坐标相同,纵坐标相反.
仿例
请在右图中的平面直角坐标系中画一个平行
四边形,写出它的四个顶点的坐标,然后画出这个平行四边形关于y轴的对称图形,写出对称图形四个顶点的坐标,观察对应顶点的坐标有什么变化.
知识模块三 相似
范例
如图,将△AOB缩小后得到△COD,你能求
出它们的相似比吗?
探索:如图,已知矩形ABCD四个顶点的坐标分别是A(0,0)、B(3,0)、C(3,2)、D(0,2),将这四个顶点坐标同时扩大到原来的2倍后得到一组新坐标,画出新坐标对应的点所确定的图形,看看新的图形和原图形之间有什么关系.
概括:我们看到,当一个几何图形经过某种运动改变位置后,图形上各点的坐标也发生了相应的变化,这些变化可以归纳成下表(请补充完整表格中的内容).
图形变换
关于x轴对称
关于y轴对称
关于原点对称
沿x轴向右平移a个单位
沿y轴向上平移b个单位
图形以原点为位似中心缩放4倍
运动前
点的坐标
(x,y)
运动后
点的坐标
(x,-y)
(x+a,y)
反过来,以某种方式同时改变一个几何图形上各点的坐标,也会使该图形产生相应的变换,从而改变它的位置或大小.
展示提升
1.已知点A(a,3)和B(4,b)关于y轴对称,则(a+b)2017的值为( )
A.-1 B.1 C.72017 D.-72017
A
2.平面直角坐标系中,A(-2,1),B(1,-2),将线段AB平移得到A′B′,且A′(1,3),则B′的坐标为________ .
3.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为
B′(4,0)
则A′的坐标为:__________________.
(4,6)或(-4,-6)
课堂小结
图形左右移动时,对应的横坐标左减右加,纵坐标不变.
图形上下移动时,对应的横坐标不变,纵坐标上加下减.
对应点关于x轴对称.即对应点的横坐标相等、纵坐标互为相反数.
对应点关于 y 轴对称.即对应点的横坐标互为相反数、纵坐标相等.
规律:对应点关于原点对称.即对应点的横坐标和纵坐标都互为相反数.
在平面直角坐标系中,如果位似变换是以原点为位似中心,
相似比为k,那么位似图形对应点的坐标的比等于k或-k.
