23.3 7 课题 相似三角形的性质课件(11张PPT)
文档属性
| 名称 | 23.3 7 课题 相似三角形的性质课件(11张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 16.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览



文档简介
相似三角形的性质
情景导入
1.什么叫相似三角形?
2.如何判定两个三角形相似?
3.相似三角形的对应边有什么特征?对应角有什么特征?
(一)自主探究
自学互研
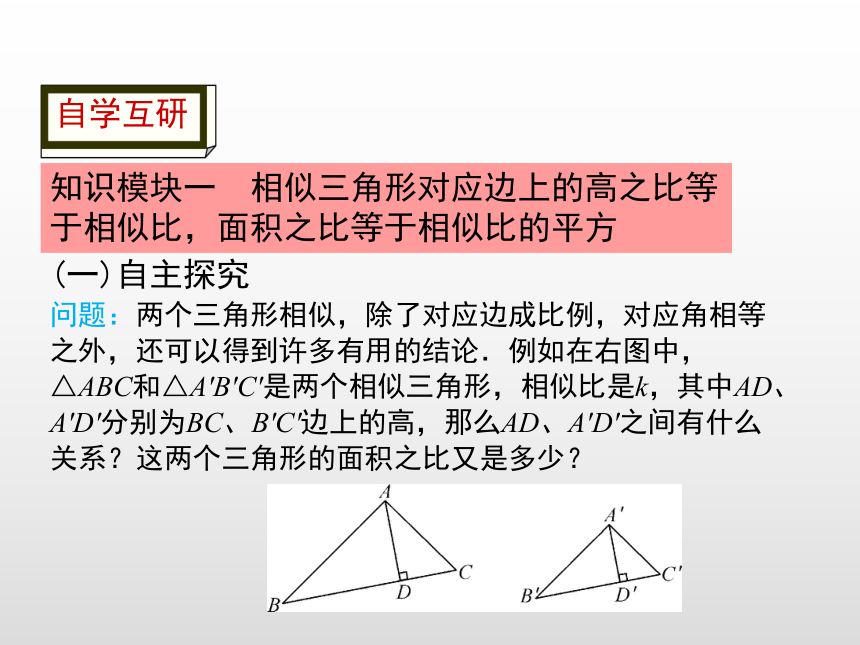
知识模块一 相似三角形对应边上的高之比等于相似比,面积之比等于相似比的平方
问题:两个三角形相似,除了对应边成比例,对应角相等之外,还可以得到许多有用的结论.例如在右图中,△ABC和△A′B′C′是两个相似三角形,相似比是k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?这两个三角形的面积之比又是多少?
(二)合作探究
归纳
△ABD和△A′B′D′都是直角三角形,且
∠B=∠B′,因为有两个角对应相等,所以这两个三角形相似,因此
由此可以得出结论:相似三角形对应边上的高的比等于相似比.
由此可以得出结论:相似三角形面积的比等于相似比的平方.
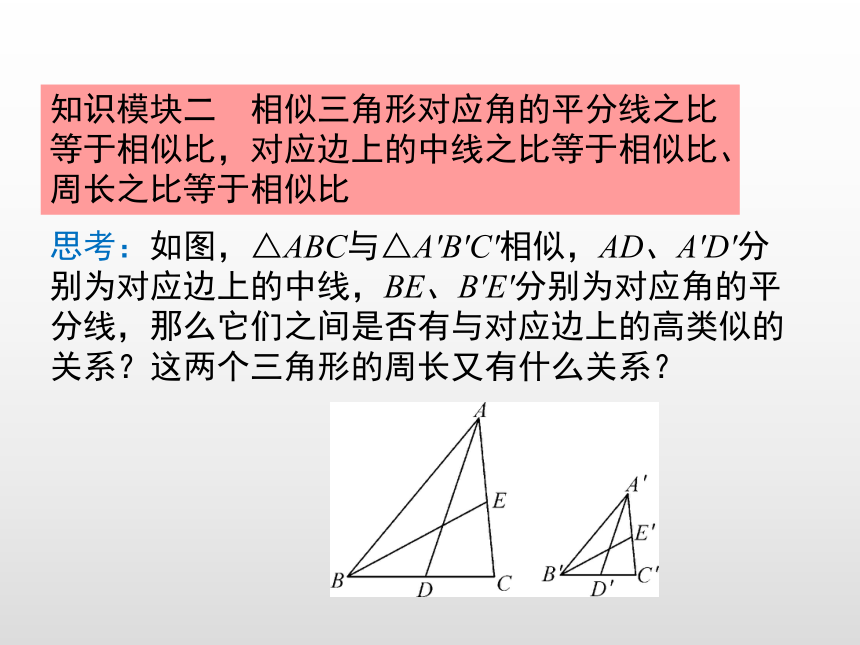
知识模块二 相似三角形对应角的平分线之比等于相似比,对应边上的中线之比等于相似比、周长之比等于相似比
思考:如图,△ABC与△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的平分线,那么它们之间是否有与对应边上的高类似的关系?这两个三角形的周长又有什么关系?
以周长为例探究一下:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′,
结论:
相似三角形对应角的平分线之比等于相似比.
相似三角形对应边上的中线之比等于相似比.
相似三角形的周长之比等于相似比.
∵△ABC∽△A′B′C′,
展示提升
1.如果两个相似多边形面积的比为1∶5,则它们的相似比为( )
A.1∶25 B.1∶5
C.1∶2.5
D
2.如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE∶S△COB=( )
A.1∶4 B.2∶3
C.1∶3 D.1∶2
A
3.已知,△ABC与△DEF相似,且对应边的比为
4.如图,在△ABC中,DE∥BC,
的面积是8,则△ABC的面积为______.
△ADE
则 ∶1, S△ABC∶S△DEF=________.
2∶1
18
5.如图,平行于BC的直线DE把△ABC分成的两部
分面积相等,则 =____
6.已知两个相似三角形两条对应边上的中线的长是3cm和5cm,那么它们的相似比是多少,对应高的比是多少?
解:3∶5,3∶5
1.相似三角形的对应高,中线,角平分线的比等于相似比.一般地,我们有:
相似三角形对应线段的比等于相似比.
2.相似三角形周长的比等于相似比;
相似多边形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方;
相似多边形面积的比等于相似比的平方.
课堂小结
情景导入
1.什么叫相似三角形?
2.如何判定两个三角形相似?
3.相似三角形的对应边有什么特征?对应角有什么特征?
(一)自主探究
自学互研
知识模块一 相似三角形对应边上的高之比等于相似比,面积之比等于相似比的平方
问题:两个三角形相似,除了对应边成比例,对应角相等之外,还可以得到许多有用的结论.例如在右图中,△ABC和△A′B′C′是两个相似三角形,相似比是k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?这两个三角形的面积之比又是多少?
(二)合作探究
归纳
△ABD和△A′B′D′都是直角三角形,且
∠B=∠B′,因为有两个角对应相等,所以这两个三角形相似,因此
由此可以得出结论:相似三角形对应边上的高的比等于相似比.
由此可以得出结论:相似三角形面积的比等于相似比的平方.
知识模块二 相似三角形对应角的平分线之比等于相似比,对应边上的中线之比等于相似比、周长之比等于相似比
思考:如图,△ABC与△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的平分线,那么它们之间是否有与对应边上的高类似的关系?这两个三角形的周长又有什么关系?
以周长为例探究一下:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′,
结论:
相似三角形对应角的平分线之比等于相似比.
相似三角形对应边上的中线之比等于相似比.
相似三角形的周长之比等于相似比.
∵△ABC∽△A′B′C′,
展示提升
1.如果两个相似多边形面积的比为1∶5,则它们的相似比为( )
A.1∶25 B.1∶5
C.1∶2.5
D
2.如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE∶S△COB=( )
A.1∶4 B.2∶3
C.1∶3 D.1∶2
A
3.已知,△ABC与△DEF相似,且对应边的比为
4.如图,在△ABC中,DE∥BC,
的面积是8,则△ABC的面积为______.
△ADE
则 ∶1, S△ABC∶S△DEF=________.
2∶1
18
5.如图,平行于BC的直线DE把△ABC分成的两部
分面积相等,则 =____
6.已知两个相似三角形两条对应边上的中线的长是3cm和5cm,那么它们的相似比是多少,对应高的比是多少?
解:3∶5,3∶5
1.相似三角形的对应高,中线,角平分线的比等于相似比.一般地,我们有:
相似三角形对应线段的比等于相似比.
2.相似三角形周长的比等于相似比;
相似多边形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方;
相似多边形面积的比等于相似比的平方.
课堂小结
