小学数学浙教版五年级上4.13三角形的面积 教案
文档属性
| 名称 | 小学数学浙教版五年级上4.13三角形的面积 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 121.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览

文档简介
《三角形的面积》教学设计
教学目标:1、经历三角形面积计算的探索和推导过程,准确理解三角形面积的计算公式。
2、能运用三角形面积计算公式进行有关计算,运用所学知识解决实际问题。
3、在探索过程中,体会平面图形间的相互转化和相互联系,进一步体会转化的数学思想方法。
教学重点:引导学生探索三角形的面积计算公式,并能运用知识进行准确计算。
教学难点:引导学生在探索过程中发现图形间的内在联系及推导说理。
教学过程:
一、复习引入
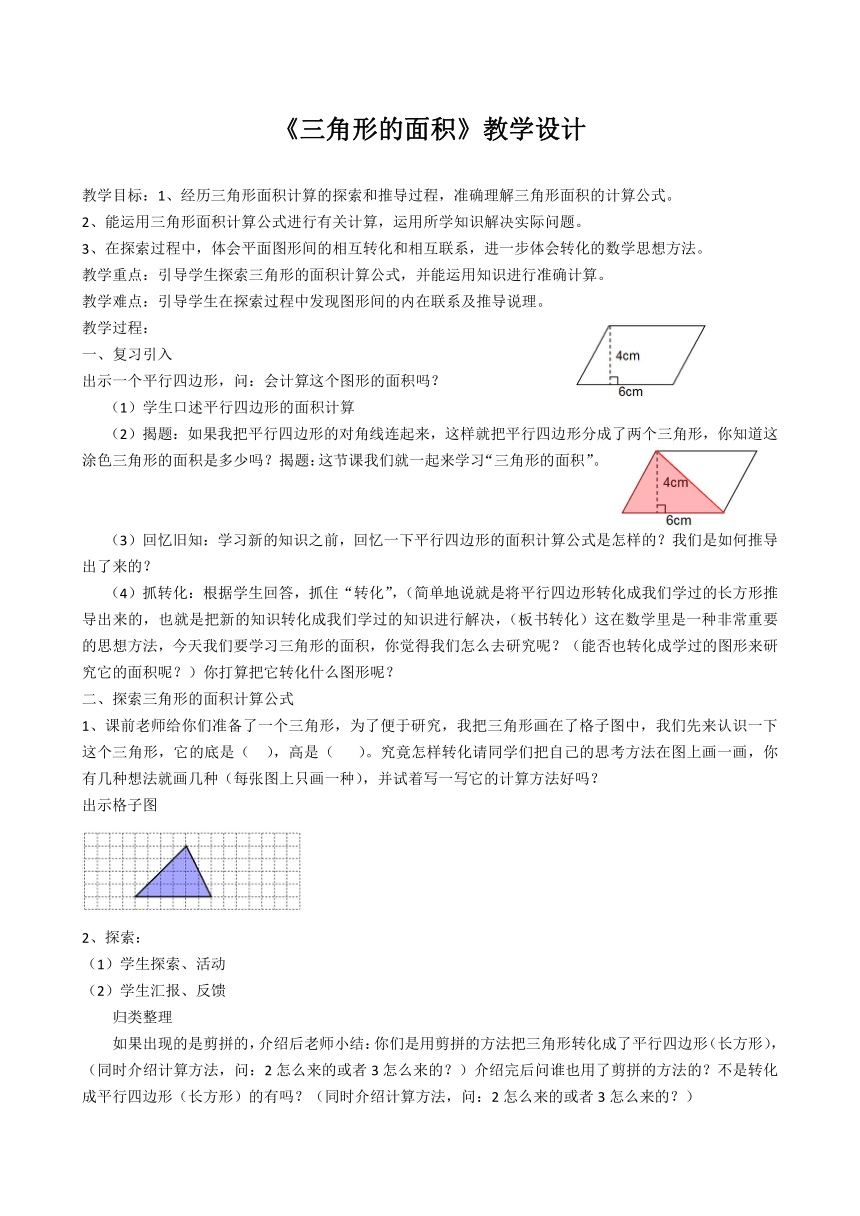
出示一个平行四边形,问:会计算这个图形的面积吗?
(1)学生口述平行四边形的面积计算
(2)揭题:如果我把平行四边形的对角线连起来,这样就把平行四边形分成了两个三角形,你知道这涂色三角形的面积是多少吗?揭题:这节课我们就一起来学习“三角形的面积”。
(3)回忆旧知:学习新的知识之前,回忆一下平行四边形的面积计算公式是怎样的?我们是如何推导出了来的?
(4)抓转化:根据学生回答,抓住“转化”,(简单地说就是将平行四边形转化成我们学过的长方形推导出来的,也就是把新的知识转化成我们学过的知识进行解决,(板书转化)这在数学里是一种非常重要的思想方法,今天我们要学习三角形的面积,你觉得我们怎么去研究呢?(能否也转化成学过的图形来研究它的面积呢?)你打算把它转化什么图形呢?
二、探索三角形的面积计算公式
1、课前老师给你们准备了一个三角形,为了便于研究,我把三角形画在了格子图中,我们先来认识一下这个三角形,它的底是( ),高是( )。究竟怎样转化请同学们把自己的思考方法在图上画一画,你有几种想法就画几种(每张图上只画一种),并试着写一写它的计算方法好吗?
出示格子图
2、探索:
(1)学生探索、活动
(2)学生汇报、反馈
归类整理
如果出现的是剪拼的,介绍后老师小结:你们是用剪拼的方法把三角形转化成了平行四边形(长方形),(同时介绍计算方法,问:2怎么来的或者3怎么来的?)介绍完后问谁也用了剪拼的方法的?不是转化成平行四边形(长方形)的有吗?(同时介绍计算方法,问:2怎么来的或者3怎么来的?)
然后再问还有不同的方法吗?
如果出现的是拼成平行四边形的方法,介绍后老师小结:你们是用拼的方法把两个三角形拼成了一个平行四边形,(介绍计算方法)然后再问还有不同的方法吗?
小结:刚才同学们有的用6×4÷2、6×(4÷2)、(6÷2)×4,其实这些方法我们都可以用6×4÷2来计算。
这里的6就是原来三角形的( ),4就是原来三角形的( )所以三角形的面积就等于底×高÷2(板书)
回过头来,你能结合这种方法(拼的方法)说一说我们是如何推导出三角形的面积计算公式的?(谁能把刚才的过程完整的说一下)
经过同学们的努力,我们成功地推导出了三角形的面积计算公式,我们一起来读一遍。
介绍字母表达式,用字母s表示三角形的面积,a和h分别表示三角形的底和高,那么三角形的面积计算公式可以怎么表示?(板书:s=ah÷2)
三、巩固练习
在我们生活中会有各种三角形,看,你会计算它们的面积吗?
学生先计算(先规范书写格式),求了这4个三角形的面积,你有什么想说的?(它们的形状各不相同,怎么它们的面积都可以用2×4÷2,这其中有什么奥秘吗?)
让学生去揭示它们的底都是2cm,高都是4cm,所以它们的面积都是( )×( )÷2=( )c㎡得出等底等高的三角形面积相等。
2、求出下列各三角形的面积(单位:cm)
交流反馈:有的同学对第四个图形有疑问,我们把这个图形放一放,待会再来讨论,先校对一下前面三个三角形的面积是怎么算的好吗?
第一个突出格式(板书)和÷2,
第二个突出底和高的对应
第三个突出底和高的对应,只要找到对应的底和高都可以算
现在我来看第四个三角形:现在对这个三角形你还有疑问吗?能用“5×4÷2”来计算吗?
那需要给你们补充什么条件?(高或底,就给你这条高的长度,会算了吗?那你知道4cm所对应的底是多少吗?知道它的面积又能求出哪些东西?)
拓展题:
先填表,问:填完表格,你有什么发现?为什么加3?这其中隐藏着什么秘密呢?请同学们讨论一下:三角形的底、高、面积中,哪两个变化了?哪一个没有变?两个变化的又是怎么变的?它们之间有什么关系?(得出,一个三角形,如果底不变,面积随着高的变化而变化,或者,高变大了,面积也增加了,进而追问,高增加了,面积是怎样增加的?:高扩大几倍,面积就扩大几倍)
四、课堂小结
这节课我们研究了哪些内容?三角形面积的计算方法是什么?怎么研究出来的?
附:板书设计
三角形的面积
转化
6×4÷2 6×(4÷2) (6÷2)×4
6×4÷2
三角形的面积=底×高÷2
S=ah÷2
教学目标:1、经历三角形面积计算的探索和推导过程,准确理解三角形面积的计算公式。
2、能运用三角形面积计算公式进行有关计算,运用所学知识解决实际问题。
3、在探索过程中,体会平面图形间的相互转化和相互联系,进一步体会转化的数学思想方法。
教学重点:引导学生探索三角形的面积计算公式,并能运用知识进行准确计算。
教学难点:引导学生在探索过程中发现图形间的内在联系及推导说理。
教学过程:
一、复习引入
出示一个平行四边形,问:会计算这个图形的面积吗?
(1)学生口述平行四边形的面积计算
(2)揭题:如果我把平行四边形的对角线连起来,这样就把平行四边形分成了两个三角形,你知道这涂色三角形的面积是多少吗?揭题:这节课我们就一起来学习“三角形的面积”。
(3)回忆旧知:学习新的知识之前,回忆一下平行四边形的面积计算公式是怎样的?我们是如何推导出了来的?
(4)抓转化:根据学生回答,抓住“转化”,(简单地说就是将平行四边形转化成我们学过的长方形推导出来的,也就是把新的知识转化成我们学过的知识进行解决,(板书转化)这在数学里是一种非常重要的思想方法,今天我们要学习三角形的面积,你觉得我们怎么去研究呢?(能否也转化成学过的图形来研究它的面积呢?)你打算把它转化什么图形呢?
二、探索三角形的面积计算公式
1、课前老师给你们准备了一个三角形,为了便于研究,我把三角形画在了格子图中,我们先来认识一下这个三角形,它的底是( ),高是( )。究竟怎样转化请同学们把自己的思考方法在图上画一画,你有几种想法就画几种(每张图上只画一种),并试着写一写它的计算方法好吗?
出示格子图
2、探索:
(1)学生探索、活动
(2)学生汇报、反馈
归类整理
如果出现的是剪拼的,介绍后老师小结:你们是用剪拼的方法把三角形转化成了平行四边形(长方形),(同时介绍计算方法,问:2怎么来的或者3怎么来的?)介绍完后问谁也用了剪拼的方法的?不是转化成平行四边形(长方形)的有吗?(同时介绍计算方法,问:2怎么来的或者3怎么来的?)
然后再问还有不同的方法吗?
如果出现的是拼成平行四边形的方法,介绍后老师小结:你们是用拼的方法把两个三角形拼成了一个平行四边形,(介绍计算方法)然后再问还有不同的方法吗?
小结:刚才同学们有的用6×4÷2、6×(4÷2)、(6÷2)×4,其实这些方法我们都可以用6×4÷2来计算。
这里的6就是原来三角形的( ),4就是原来三角形的( )所以三角形的面积就等于底×高÷2(板书)
回过头来,你能结合这种方法(拼的方法)说一说我们是如何推导出三角形的面积计算公式的?(谁能把刚才的过程完整的说一下)
经过同学们的努力,我们成功地推导出了三角形的面积计算公式,我们一起来读一遍。
介绍字母表达式,用字母s表示三角形的面积,a和h分别表示三角形的底和高,那么三角形的面积计算公式可以怎么表示?(板书:s=ah÷2)
三、巩固练习
在我们生活中会有各种三角形,看,你会计算它们的面积吗?
学生先计算(先规范书写格式),求了这4个三角形的面积,你有什么想说的?(它们的形状各不相同,怎么它们的面积都可以用2×4÷2,这其中有什么奥秘吗?)
让学生去揭示它们的底都是2cm,高都是4cm,所以它们的面积都是( )×( )÷2=( )c㎡得出等底等高的三角形面积相等。
2、求出下列各三角形的面积(单位:cm)
交流反馈:有的同学对第四个图形有疑问,我们把这个图形放一放,待会再来讨论,先校对一下前面三个三角形的面积是怎么算的好吗?
第一个突出格式(板书)和÷2,
第二个突出底和高的对应
第三个突出底和高的对应,只要找到对应的底和高都可以算
现在我来看第四个三角形:现在对这个三角形你还有疑问吗?能用“5×4÷2”来计算吗?
那需要给你们补充什么条件?(高或底,就给你这条高的长度,会算了吗?那你知道4cm所对应的底是多少吗?知道它的面积又能求出哪些东西?)
拓展题:
先填表,问:填完表格,你有什么发现?为什么加3?这其中隐藏着什么秘密呢?请同学们讨论一下:三角形的底、高、面积中,哪两个变化了?哪一个没有变?两个变化的又是怎么变的?它们之间有什么关系?(得出,一个三角形,如果底不变,面积随着高的变化而变化,或者,高变大了,面积也增加了,进而追问,高增加了,面积是怎样增加的?:高扩大几倍,面积就扩大几倍)
四、课堂小结
这节课我们研究了哪些内容?三角形面积的计算方法是什么?怎么研究出来的?
附:板书设计
三角形的面积
转化
6×4÷2 6×(4÷2) (6÷2)×4
6×4÷2
三角形的面积=底×高÷2
S=ah÷2
同课章节目录
