2020年秋人教版九年级数学上册随堂练——23.1图形的旋转随堂练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练——23.1图形的旋转随堂练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 373.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览

文档简介
23.1图形的旋转随堂练习
一、选择题
1.已知点,把点绕点逆时针旋转后得到的点的坐标为(
)
A.(-2,?1)
B.(-1,?2)
C.(2,?-1)
D.(1,?-2)
2.
如图,的斜边在轴上,,含角的顶点与原点重合,直角顶点在第二象限,将绕原点顺时针旋转后得到,则点的对应点的坐标是(
)
A.
B.
C.
D.
3.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(
)
A.60°
B.90°
C.120°
D.150°
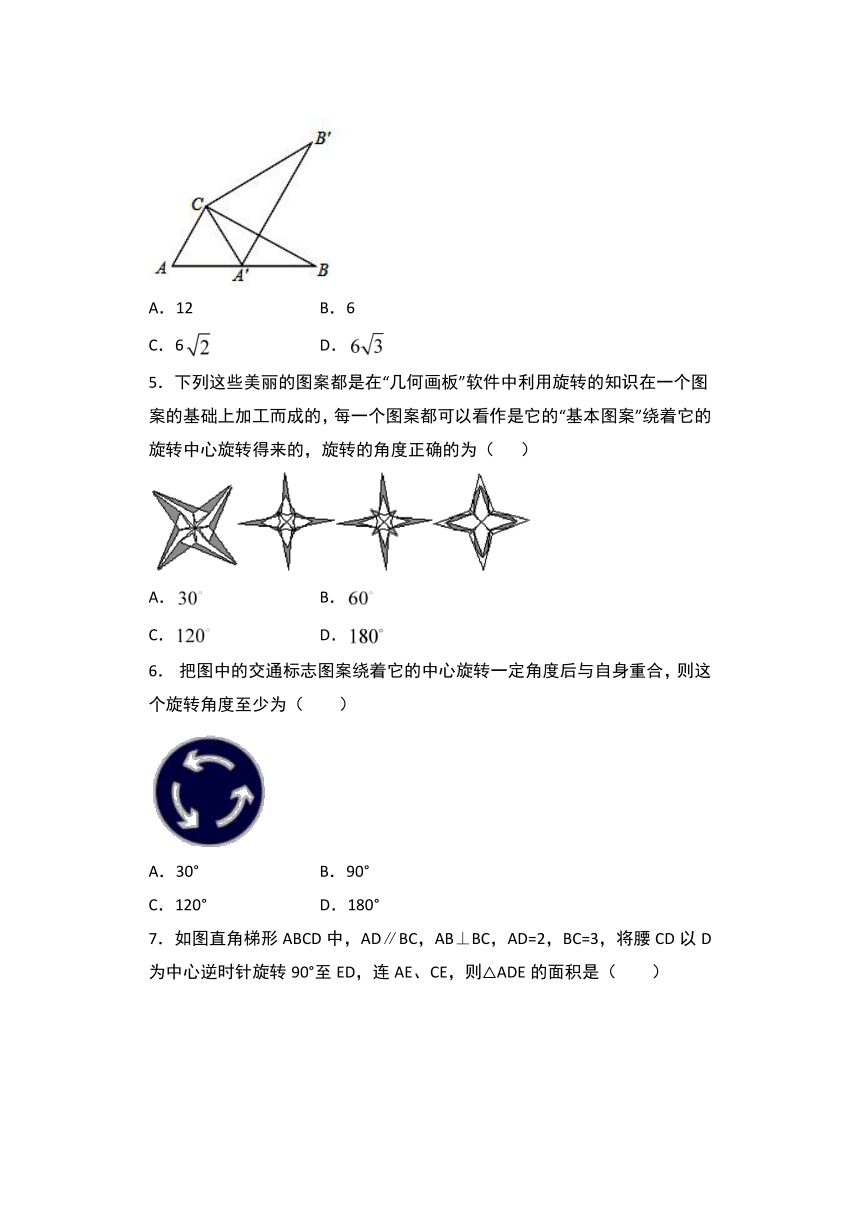
4.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A.12
B.6
C.6
D.
5.下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为(
)
A.
B.
C.
D.
6.
把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为(
)
A.30°
B.90°
C.120°
D.180°
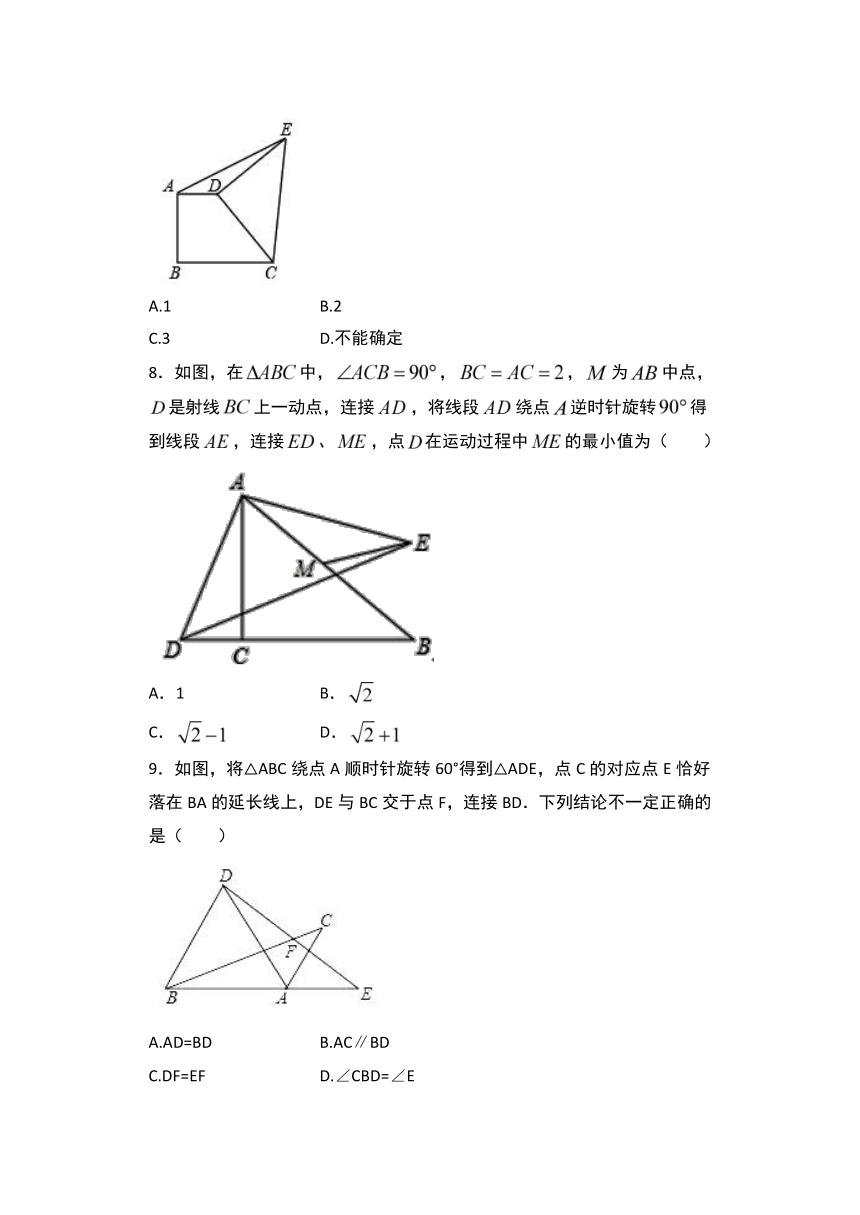
7.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1
B.2
C.3
D.不能确定
8.如图,在中,,,为中点,是射线上一动点,连接,将线段绕点逆时针旋转得到线段,连接、,点在运动过程中的最小值为( )
A.1
B.
C.
D.
9.如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
A.AD=BD
B.AC∥BD
C.DF=EF
D.∠CBD=∠E
二、填空题
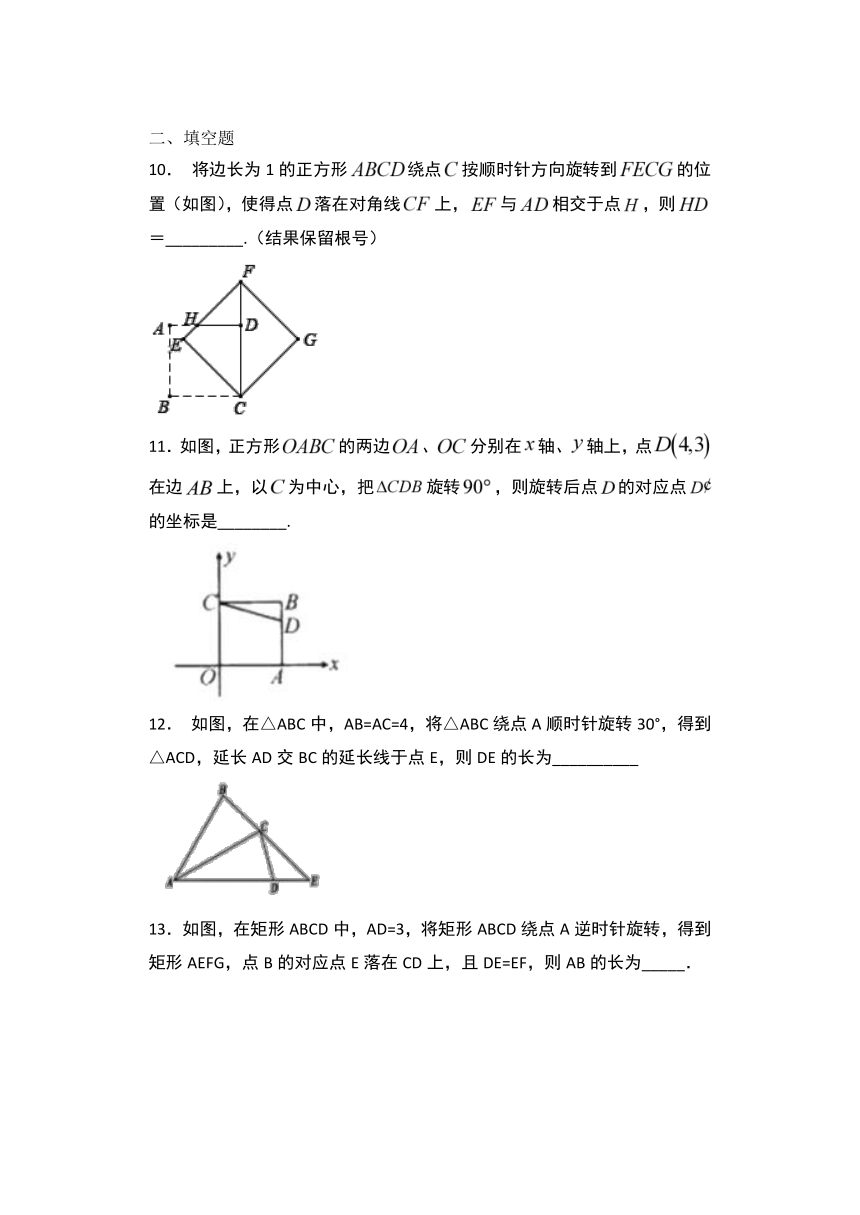
10.
将边长为1的正方形绕点按顺时针方向旋转到的位置(如图),使得点落在对角线上,与相交于点,则=_________.(结果保留根号)
11.如图,正方形的两边、分别在轴、轴上,点在边上,以为中心,把旋转,则旋转后点的对应点的坐标是________.
12.
如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
13.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.
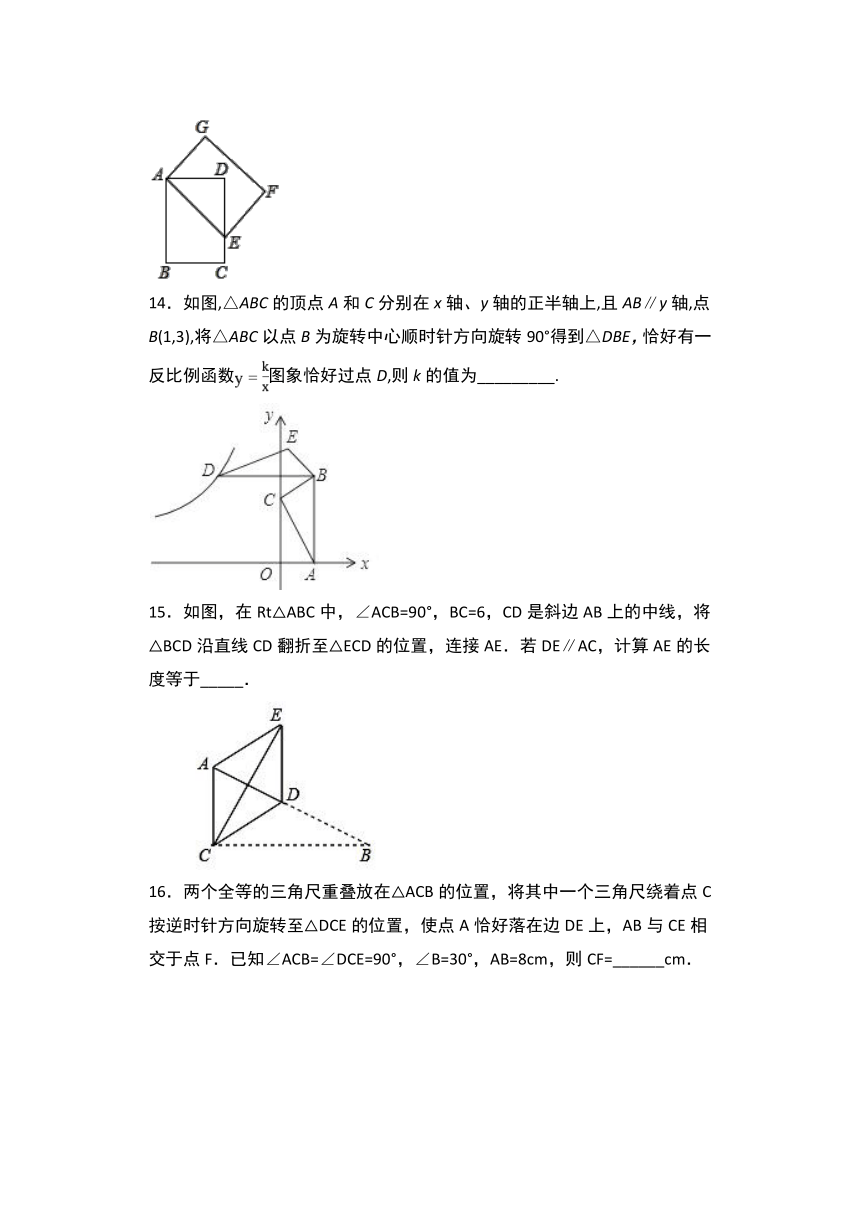
14.如图,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数图象恰好过点D,则k的值为_________.
15.如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
16.两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=______cm.
17.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接E,F.给出下列五个结论:①AP=EF;②PD=EC;③∠PFE=∠BAP;④△APD一定是等腰三角形;⑤AP⊥EF.其中正确结论的序号是_____.
三、解答题
18.
如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点,点B的对应点为点,请画出平移后的线段;
(2)将线段绕点按逆时针方向旋转,点的对应点为点,请画出旋转后的线段;
(3)连接、,求的面积.
19.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
20.如图,在中,,,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转得到线段CE,连结DE交BC于点F,连接BE.
求证:≌;
当时,求的度数.
21.四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
22.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
23.如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
24.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=
;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON=
;∠CON=
.
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
25.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
答案
1.
B
2.
A
3.
D
4.
D
5.
D
6.
C
7.
A
8.
A
9.
C
10.
11.
或
12.
13.
3
14.
-6.
15.
2
16.
17.
①③⑤
18.
解(1)线段如图所示;
(2)线段如图所示;
(3)S△
.
19.
解:证明:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,AD=OB=3,
又∵△COD是等边三角形,
∴∠ODC=60°,OD=OC=4
∴∠ADO=∠ADC﹣∠ODC=90°,
∴OA==5
20.
解由题意可知:,,
,
,
,
,
在与中,
,
≌;
,,
,
由可知:,
,
,
.
21.
解
(1)
根据旋转的性质可知:△AFD≌△AEB,
所以,AE=AF=4,∠EAF=90°,∠EBA=∠FDA,
可得旋转中心为点A,旋转角度为90°或270°;
(2)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD?AE=7?4=3;
(3)BE、DF的关系为:
BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°?90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE⊥DF.
22.
(1)连接BD,
∵AB=AD,∠A=60°,∴△ABD是等边三角形,∴∠ADB=60°,DB=4,
∵42+82=(4)2,∴DB2+CD2=BC2,∴∠BDC=90°,∴∠ADC=60°+90°=150°;
(2)过B作BE⊥AD,∵∠A=60°,AB=4,∴BE=AB?sin60°=4×=2,
∴四边形ABCD的面积为:AD?EB+DB?CD=×4×2+×4×8=4+16.
23.
(1)如图1,结论:CM=EM,CM⊥EM.
理由:∵AD∥EF,AD∥BC,
∴BC∥EF,
∴∠EFM=∠HBM,
在△FME和△BMH中,
,,
∴△FME≌△BMH,
∴HM=EM,EF=BH,
∵CD=BC,
∴CE=CH,∵∠HCE=90°,HM=EM,
∴CM=ME,CM⊥EM.
(2)如图2,连接AE,
∵四边形ABCD和四边形EDGF是正方形,
∴∠FDE=45°,∠CBD=45°,
∴点B、E、D在同一条直线上,
∵∠BCF=90°,∠BEF=90°,M为AF的中点,
∴CM=AF,EM=AF,
∴CM=ME,
∵∠EFD=45°,
∴∠EFC=135°,
∵CM=FM=ME,
∴∠MCF=∠MFC,∠MFE=∠MEF,
∴∠MCF+∠MEF=135°,
∴∠CME=360°-135°-135°=90°,
∴CM⊥ME.
(3)如图3,连接CF,MG,作MN⊥CD于N,
在△EDM和△GDM中,
,
∴△EDM≌△GDM,
∴ME=MG,∠MED=∠MGD,
∵M为BF的中点,FG∥MN∥BC,
∴GN=NC,又MN⊥CD,
∴MC=MG,
∴MD=ME,∠MCG=∠MGC,
∵∠MGC+∠MGD=180°,
∴∠MCG+∠MED=180°,
∴∠CME+∠CDE=180°,
∵∠CDE=90°,
∴∠CME=90°,
∴(1)中的结论成立.
24.
(1)∠MOC=∠MON﹣∠BOC=90°﹣65°=25°,
故答案为:25°;
(2)∵OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=2×65°=130°,
∴旋转角∠BON=∠MOB﹣∠MON=130°﹣90°=40°,
∠CON=∠BOC﹣∠BON=65°﹣40°=25°,
故答案为:40°,25°;
(3)∵∠NOC=5°,∠BOC=65°,
∴∠BON=∠NOC+∠BOC=70°,
∵点O为直线AB上一点,
∴∠AOB=180°,
∵∠MON=90°,
∴∠AOM=∠AOB﹣∠MON﹣∠BON=180°﹣90°﹣70°=20°.
25.
(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
,
∴△EAB≌△DAC.
∴∠AEB=∠ADC.
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=105°.
∴∠BED=45°.
一、选择题
1.已知点,把点绕点逆时针旋转后得到的点的坐标为(
)
A.(-2,?1)
B.(-1,?2)
C.(2,?-1)
D.(1,?-2)
2.
如图,的斜边在轴上,,含角的顶点与原点重合,直角顶点在第二象限,将绕原点顺时针旋转后得到,则点的对应点的坐标是(
)
A.
B.
C.
D.
3.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(
)
A.60°
B.90°
C.120°
D.150°
4.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A.12
B.6
C.6
D.
5.下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为(
)
A.
B.
C.
D.
6.
把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为(
)
A.30°
B.90°
C.120°
D.180°
7.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
A.1
B.2
C.3
D.不能确定
8.如图,在中,,,为中点,是射线上一动点,连接,将线段绕点逆时针旋转得到线段,连接、,点在运动过程中的最小值为( )
A.1
B.
C.
D.
9.如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
A.AD=BD
B.AC∥BD
C.DF=EF
D.∠CBD=∠E
二、填空题
10.
将边长为1的正方形绕点按顺时针方向旋转到的位置(如图),使得点落在对角线上,与相交于点,则=_________.(结果保留根号)
11.如图,正方形的两边、分别在轴、轴上,点在边上,以为中心,把旋转,则旋转后点的对应点的坐标是________.
12.
如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
13.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.
14.如图,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数图象恰好过点D,则k的值为_________.
15.如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
16.两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=______cm.
17.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接E,F.给出下列五个结论:①AP=EF;②PD=EC;③∠PFE=∠BAP;④△APD一定是等腰三角形;⑤AP⊥EF.其中正确结论的序号是_____.
三、解答题
18.
如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点,点B的对应点为点,请画出平移后的线段;
(2)将线段绕点按逆时针方向旋转,点的对应点为点,请画出旋转后的线段;
(3)连接、,求的面积.
19.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
20.如图,在中,,,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转得到线段CE,连结DE交BC于点F,连接BE.
求证:≌;
当时,求的度数.
21.四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
22.如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4,CD=8.
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
23.如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
24.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC=
;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON=
;∠CON=
.
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.
25.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
答案
1.
B
2.
A
3.
D
4.
D
5.
D
6.
C
7.
A
8.
A
9.
C
10.
11.
或
12.
13.
3
14.
-6.
15.
2
16.
17.
①③⑤
18.
解(1)线段如图所示;
(2)线段如图所示;
(3)S△
.
19.
解:证明:(1)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,AD=OB=3,
又∵△COD是等边三角形,
∴∠ODC=60°,OD=OC=4
∴∠ADO=∠ADC﹣∠ODC=90°,
∴OA==5
20.
解由题意可知:,,
,
,
,
,
在与中,
,
≌;
,,
,
由可知:,
,
,
.
21.
解
(1)
根据旋转的性质可知:△AFD≌△AEB,
所以,AE=AF=4,∠EAF=90°,∠EBA=∠FDA,
可得旋转中心为点A,旋转角度为90°或270°;
(2)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD?AE=7?4=3;
(3)BE、DF的关系为:
BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°?90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE⊥DF.
22.
(1)连接BD,
∵AB=AD,∠A=60°,∴△ABD是等边三角形,∴∠ADB=60°,DB=4,
∵42+82=(4)2,∴DB2+CD2=BC2,∴∠BDC=90°,∴∠ADC=60°+90°=150°;
(2)过B作BE⊥AD,∵∠A=60°,AB=4,∴BE=AB?sin60°=4×=2,
∴四边形ABCD的面积为:AD?EB+DB?CD=×4×2+×4×8=4+16.
23.
(1)如图1,结论:CM=EM,CM⊥EM.
理由:∵AD∥EF,AD∥BC,
∴BC∥EF,
∴∠EFM=∠HBM,
在△FME和△BMH中,
,,
∴△FME≌△BMH,
∴HM=EM,EF=BH,
∵CD=BC,
∴CE=CH,∵∠HCE=90°,HM=EM,
∴CM=ME,CM⊥EM.
(2)如图2,连接AE,
∵四边形ABCD和四边形EDGF是正方形,
∴∠FDE=45°,∠CBD=45°,
∴点B、E、D在同一条直线上,
∵∠BCF=90°,∠BEF=90°,M为AF的中点,
∴CM=AF,EM=AF,
∴CM=ME,
∵∠EFD=45°,
∴∠EFC=135°,
∵CM=FM=ME,
∴∠MCF=∠MFC,∠MFE=∠MEF,
∴∠MCF+∠MEF=135°,
∴∠CME=360°-135°-135°=90°,
∴CM⊥ME.
(3)如图3,连接CF,MG,作MN⊥CD于N,
在△EDM和△GDM中,
,
∴△EDM≌△GDM,
∴ME=MG,∠MED=∠MGD,
∵M为BF的中点,FG∥MN∥BC,
∴GN=NC,又MN⊥CD,
∴MC=MG,
∴MD=ME,∠MCG=∠MGC,
∵∠MGC+∠MGD=180°,
∴∠MCG+∠MED=180°,
∴∠CME+∠CDE=180°,
∵∠CDE=90°,
∴∠CME=90°,
∴(1)中的结论成立.
24.
(1)∠MOC=∠MON﹣∠BOC=90°﹣65°=25°,
故答案为:25°;
(2)∵OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=2×65°=130°,
∴旋转角∠BON=∠MOB﹣∠MON=130°﹣90°=40°,
∠CON=∠BOC﹣∠BON=65°﹣40°=25°,
故答案为:40°,25°;
(3)∵∠NOC=5°,∠BOC=65°,
∴∠BON=∠NOC+∠BOC=70°,
∵点O为直线AB上一点,
∴∠AOB=180°,
∵∠MON=90°,
∴∠AOM=∠AOB﹣∠MON﹣∠BON=180°﹣90°﹣70°=20°.
25.
(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
,
∴△EAB≌△DAC.
∴∠AEB=∠ADC.
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=105°.
∴∠BED=45°.
同课章节目录
