2020年秋人教版九年级数学上册随堂练——23.1图形的旋转提升练习(word版,含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练——23.1图形的旋转提升练习(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 336.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 14:07:35 | ||
图片预览

文档简介
23.1图形的旋转提升练习
一、选择题
1.
如图,在平面直角坐标系中,将点绕原点顺时针旋转90°得到点,则的坐标为(
)
A.
B.
C.
D.
2.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为(
)
A.(1,-1)
B.(-1,-1)
C.(,0)
D.(0,-)
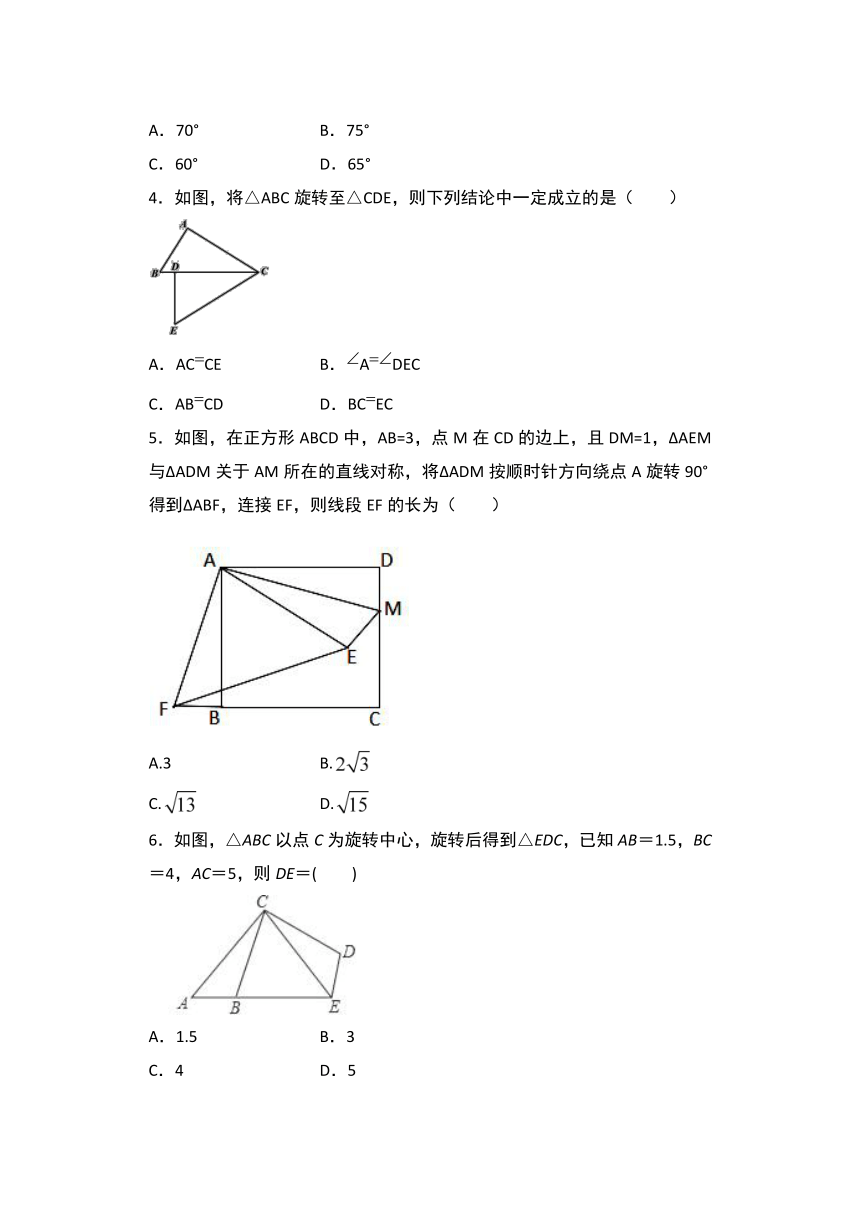
3.如图,△ODC是由△OAB统点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70°
B.75°
C.60°
D.65°
4.如图,将△ABC旋转至△CDE,则下列结论中一定成立的是(
)
A.ACCE
B.ADEC
C.ABCD
D.BCEC
5.如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为(
)
A.3
B.
C.
D.
6.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
A.1.5
B.3
C.4
D.5
7.
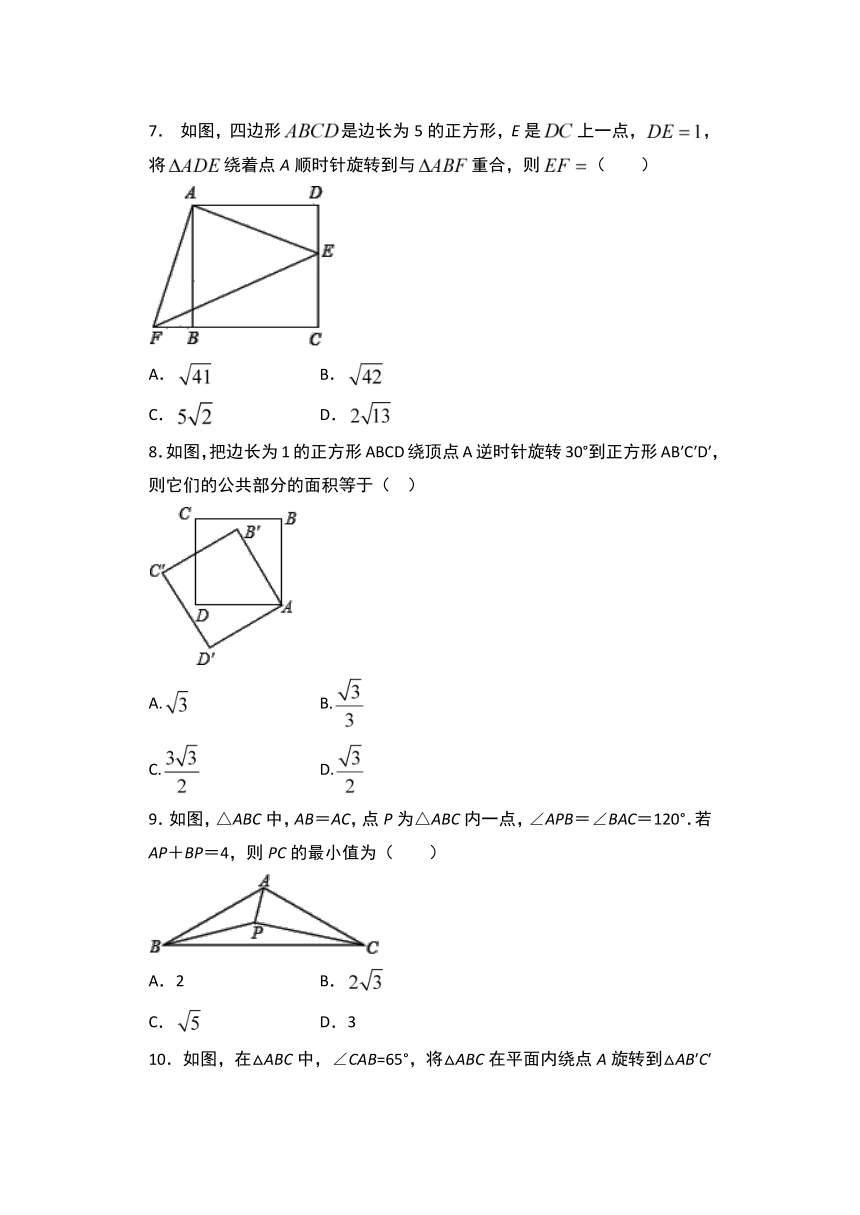
如图,四边形是边长为5的正方形,E是上一点,,将绕着点A顺时针旋转到与重合,则(
)
A.
B.
C.
D.
8.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于(??
)
A.
B.
C.
D.
9.如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为(
)
A.2
B.
C.
D.3
10.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30°
B.40°
C.50°
D.65°
二、填空题
11.
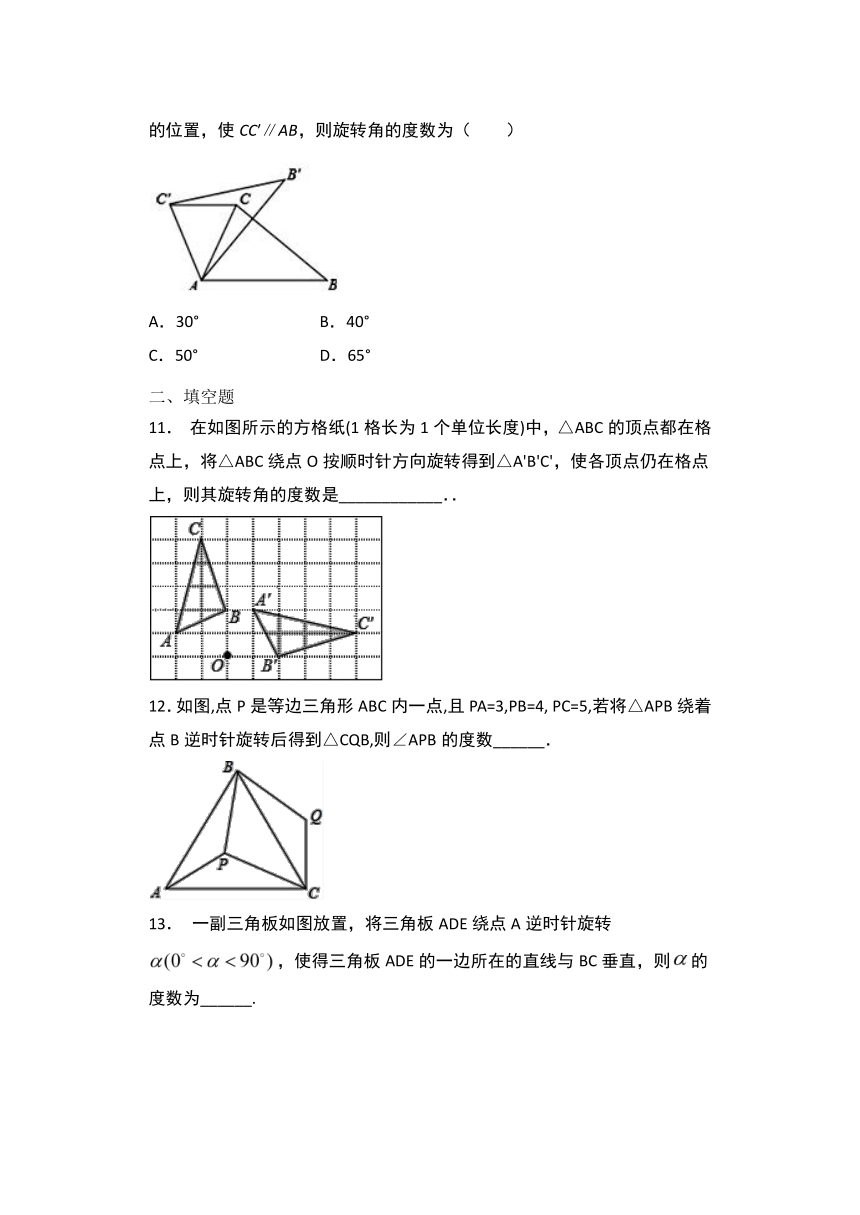
在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是____________..
12.如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
13.
一副三角板如图放置,将三角板ADE绕点A逆时针旋转,使得三角板ADE的一边所在的直线与BC垂直,则的度数为______.
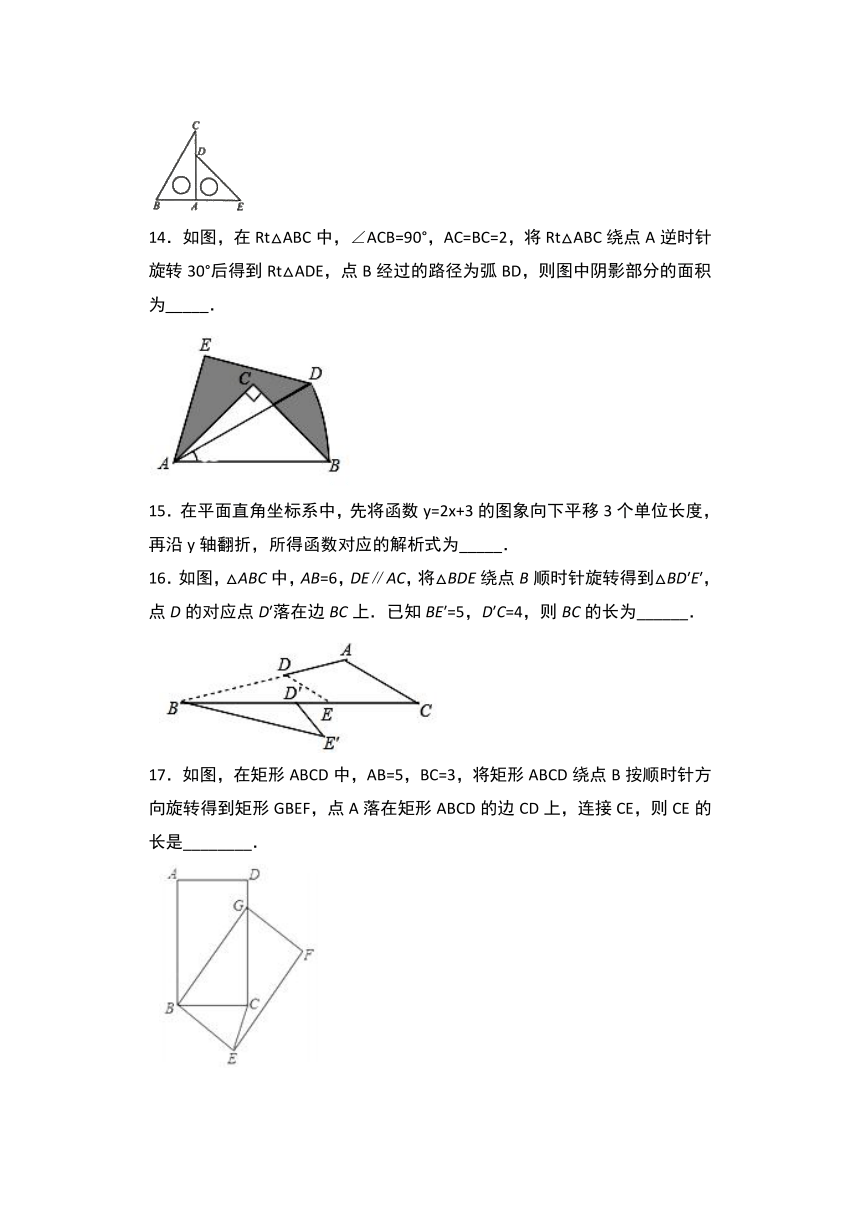
14.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为_____.
15.在平面直角坐标系中,先将函数y=2x+3的图象向下平移3个单位长度,再沿y轴翻折,所得函数对应的解析式为_____.
16.如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为______.
17.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是________.
三、解答题
18.如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,
AB=AD.
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
19.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣1,1),B(﹣4,1),C(﹣3,3).
(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;并判断以O,A1,B为顶点的三角形的形状(直接写出结果);
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2,并求出点C旋转到C2所经过的路径长.
20.
(1)问题发现?
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.?
填空:线段AD,BE之间的关系为?
.
(2)拓展探究?
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.?
(3)解决问题?
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.?
21.
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
22.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
23.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.
24.如图,在正方形ABCD中,E为DC边上的点,连接BE,将绕点C顺时针方向旋转得到△DCF,连结EF,若,求的度数.
25.四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)若BC=12,DE=5,求△AEF的面积.
26.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且,将绕点D逆时针旋转,得到.
求证:.
当时,求EF的长.
答案
1.
D
2.
B
3.
B
4.
D
5.
C
6.
A
7.
D
8.
B
9.
B
10.
C
11.
90°
12.
150°
13.
15°或60°.
14.
15.
y=-2x.
16.
17.
18.
解:(1)、∵∠BAC=∠DAE,AB=AD,∠B=∠D,∴△ABD≌△ADE.
(2)、∵△ABC≌△ADE,
∴AC与AE是一组对应边,
∴∠CAE的旋转角,
∵AE=AC,∠AEC=75°,
∴∠ACE=∠AEC=75°,
∴∠CAE=180°—75°—75°=30°
19.
解
(1)如图,△A1B1C1为所作,
∵,,,
∴,
∴以O,A1,B为顶点的三角形为等腰直角三角形;
(2)如图,△A2B2C2为所作,点C旋转到C2所经过的路径长.
20.
解(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
故答案为AD=BE,AD⊥BE.
(2)结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-3,
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3,
∴5-3≤BE≤5+3,
即5-3≤PC≤5+3.
21.
解
(1)【操作发现】60.
理由:∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°.
(2)【类比探究】证明:如图,以PA为边长作等边△PAD,使
P,D分别在,AC的两侧,连接CD.
∵∠BAC=∠PAD=60°
∴∠BAP=∠CAD.
∵AB=AC,AP=AD,
∴△PAB≌△DAC(SAS),
∴BP=CD.
在△PCD中,∵PD+CD>PC.
又∵AP=PD,
∴AP+BP>PC.
∴以PA,PB,PC的长为三边必能组成三角形.
(3)【解决问题】如图,将△APB绕点A按逆时针方向旋转60°,得到△AP′C,
∴∠AP′C=∠APB=360°-90°-120°=150°,
AP=AP′,∠PAP′=
60?∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=150°-60°=90°,
∠P′PC=∠APC-∠APP′=30°,
∴PP′=,即AP=.
∵∠APC=90°,AC=,
∴AP?
+PC?
=AC?,即,
∴PC=2(舍负),∴AP=,∴.
(4)【拓展应用】如图,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD,BE.
∵将△APC绕点C顺时针旋转60°得到△EDC,
∴△APC≌△EDC,∠PCD=60°
∴∠ACP=∠ECD,AC=EC=4,
∴∠ACB=∠ACP+∠PCB=∠ECD+∠PCB=30°,
∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°.
在Rt△BCE中,∵BC=5,CE=4,
∴,
当P,D在BE上时,PA+PB+PC=BE,此时PA+PB+PC取最小值,为.
22.
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中
∴△BAP≌△CAQ(SAS),
∴PB=QC;
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
23.
(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,AD=AB=10,
∴∠ABD=45°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠BDF=∠ABD=45°;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴,
∵AB=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.
24.
△DCF是△BCE旋转得到的图形,
,,,
.
.
25.
解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中,
∵
,
∴△ADE≌△ABF(SAS);
(2)∵BC=12,∴AD=12,
在Rt△ADE中,DE=5,AD=12,
∴AE==13,(勾股定理)
∵△ABF可以由△ADE绕旋转中心?A点,按顺时针方向旋转90°得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=AE2=×169=84.5.
26.
(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
试卷第6页,总6页
一、选择题
1.
如图,在平面直角坐标系中,将点绕原点顺时针旋转90°得到点,则的坐标为(
)
A.
B.
C.
D.
2.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为(
)
A.(1,-1)
B.(-1,-1)
C.(,0)
D.(0,-)
3.如图,△ODC是由△OAB统点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,则∠A的度数为( )
A.70°
B.75°
C.60°
D.65°
4.如图,将△ABC旋转至△CDE,则下列结论中一定成立的是(
)
A.ACCE
B.ADEC
C.ABCD
D.BCEC
5.如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为(
)
A.3
B.
C.
D.
6.如图,△ABC以点C为旋转中心,旋转后得到△EDC,已知AB=1.5,BC=4,AC=5,则DE=( )
A.1.5
B.3
C.4
D.5
7.
如图,四边形是边长为5的正方形,E是上一点,,将绕着点A顺时针旋转到与重合,则(
)
A.
B.
C.
D.
8.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于(??
)
A.
B.
C.
D.
9.如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为(
)
A.2
B.
C.
D.3
10.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30°
B.40°
C.50°
D.65°
二、填空题
11.
在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是____________..
12.如图,点P是等边三角形ABC内一点,且PA=3,PB=4,
PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
13.
一副三角板如图放置,将三角板ADE绕点A逆时针旋转,使得三角板ADE的一边所在的直线与BC垂直,则的度数为______.
14.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为_____.
15.在平面直角坐标系中,先将函数y=2x+3的图象向下平移3个单位长度,再沿y轴翻折,所得函数对应的解析式为_____.
16.如图,△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BD′E′,点D的对应点D′落在边BC上.已知BE′=5,D′C=4,则BC的长为______.
17.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是________.
三、解答题
18.如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D,
AB=AD.
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
19.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(﹣1,1),B(﹣4,1),C(﹣3,3).
(1)将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;并判断以O,A1,B为顶点的三角形的形状(直接写出结果);
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2,并求出点C旋转到C2所经过的路径长.
20.
(1)问题发现?
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.?
填空:线段AD,BE之间的关系为?
.
(2)拓展探究?
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.?
(3)解决问题?
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.?
21.
(1)(操作发现)
如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=____度;
(2)(类比探究)
如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形:
(3)(解决问题)
如图③,在边长为的等边三角形ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC的面积;
(4)(拓展应用)
图④是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.
22.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
23.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.
24.如图,在正方形ABCD中,E为DC边上的点,连接BE,将绕点C顺时针方向旋转得到△DCF,连结EF,若,求的度数.
25.四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)若BC=12,DE=5,求△AEF的面积.
26.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且,将绕点D逆时针旋转,得到.
求证:.
当时,求EF的长.
答案
1.
D
2.
B
3.
B
4.
D
5.
C
6.
A
7.
D
8.
B
9.
B
10.
C
11.
90°
12.
150°
13.
15°或60°.
14.
15.
y=-2x.
16.
17.
18.
解:(1)、∵∠BAC=∠DAE,AB=AD,∠B=∠D,∴△ABD≌△ADE.
(2)、∵△ABC≌△ADE,
∴AC与AE是一组对应边,
∴∠CAE的旋转角,
∵AE=AC,∠AEC=75°,
∴∠ACE=∠AEC=75°,
∴∠CAE=180°—75°—75°=30°
19.
解
(1)如图,△A1B1C1为所作,
∵,,,
∴,
∴以O,A1,B为顶点的三角形为等腰直角三角形;
(2)如图,△A2B2C2为所作,点C旋转到C2所经过的路径长.
20.
解(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
故答案为AD=BE,AD⊥BE.
(2)结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-3,
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3,
∴5-3≤BE≤5+3,
即5-3≤PC≤5+3.
21.
解
(1)【操作发现】60.
理由:∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°.
(2)【类比探究】证明:如图,以PA为边长作等边△PAD,使
P,D分别在,AC的两侧,连接CD.
∵∠BAC=∠PAD=60°
∴∠BAP=∠CAD.
∵AB=AC,AP=AD,
∴△PAB≌△DAC(SAS),
∴BP=CD.
在△PCD中,∵PD+CD>PC.
又∵AP=PD,
∴AP+BP>PC.
∴以PA,PB,PC的长为三边必能组成三角形.
(3)【解决问题】如图,将△APB绕点A按逆时针方向旋转60°,得到△AP′C,
∴∠AP′C=∠APB=360°-90°-120°=150°,
AP=AP′,∠PAP′=
60?∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=150°-60°=90°,
∠P′PC=∠APC-∠APP′=30°,
∴PP′=,即AP=.
∵∠APC=90°,AC=,
∴AP?
+PC?
=AC?,即,
∴PC=2(舍负),∴AP=,∴.
(4)【拓展应用】如图,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD,BE.
∵将△APC绕点C顺时针旋转60°得到△EDC,
∴△APC≌△EDC,∠PCD=60°
∴∠ACP=∠ECD,AC=EC=4,
∴∠ACB=∠ACP+∠PCB=∠ECD+∠PCB=30°,
∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°.
在Rt△BCE中,∵BC=5,CE=4,
∴,
当P,D在BE上时,PA+PB+PC=BE,此时PA+PB+PC取最小值,为.
22.
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中
∴△BAP≌△CAQ(SAS),
∴PB=QC;
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
23.
(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,AD=AB=10,
∴∠ABD=45°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠BDF=∠ABD=45°;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴,
∵AB=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.
24.
△DCF是△BCE旋转得到的图形,
,,,
.
.
25.
解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中,
∵
,
∴△ADE≌△ABF(SAS);
(2)∵BC=12,∴AD=12,
在Rt△ADE中,DE=5,AD=12,
∴AE==13,(勾股定理)
∵△ABF可以由△ADE绕旋转中心?A点,按顺时针方向旋转90°得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=AE2=×169=84.5.
26.
(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
试卷第6页,总6页
同课章节目录
