2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计随堂练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册随堂练——23.3课题学习图案设计随堂练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 14:17:01 | ||
图片预览


文档简介
23.3课题学习图案设计随堂练习
一、选择题
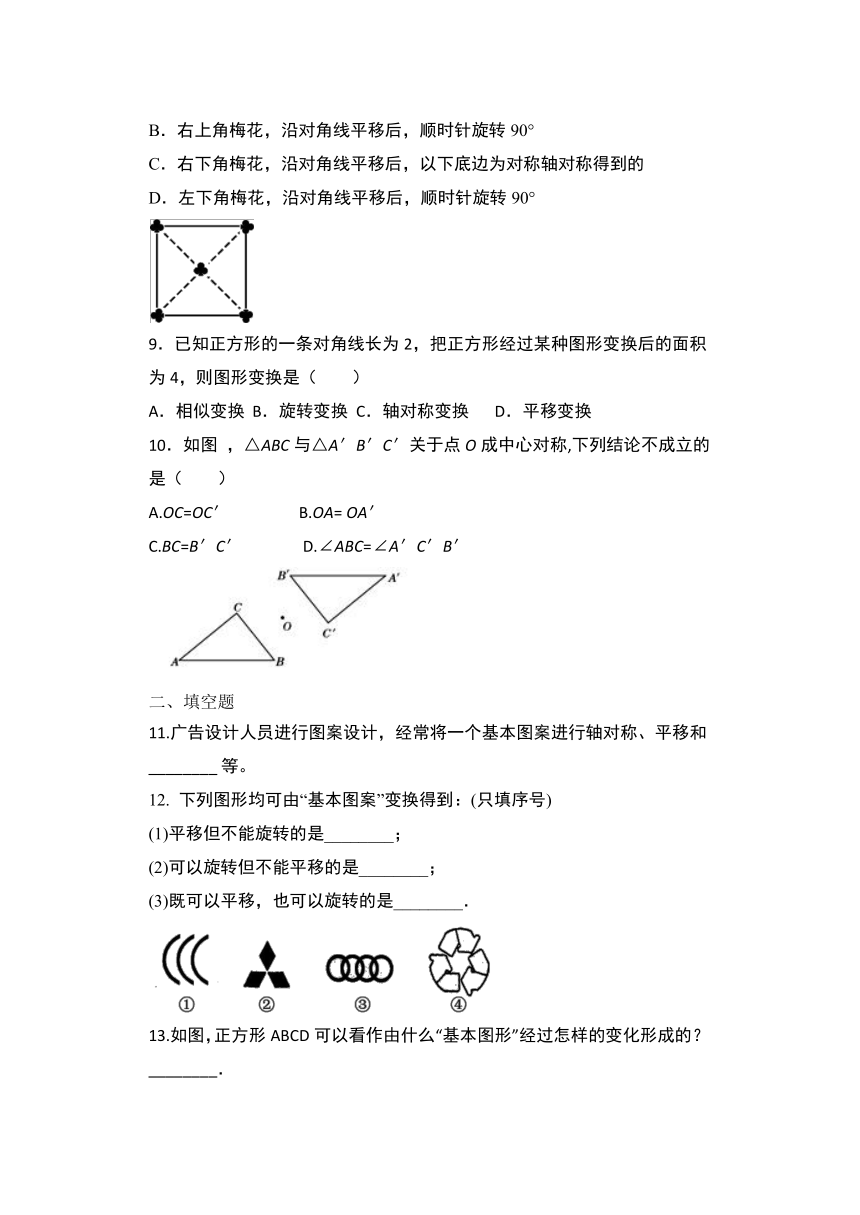
1.把一张正方形纸片如图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是(
)
2.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
A.?
B.?
C.?
D.?
3.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
4.如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )
A.5
B.6
C.4
D.7
5.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是(
)
6.下列四幅图案在设计中用到平移变换方式的是( )
A.?
B.??
C.?
D.?
7.如图,由图中所示的图案通过平移后得到的图案是( )
A.
B.
C.
D.
8.
观察如图所摆放的五朵梅花,变换中间的一朵梅花,得到四角的梅花,下列说法错误的是(
)
A.左上角梅花,只需沿对角线平移即可
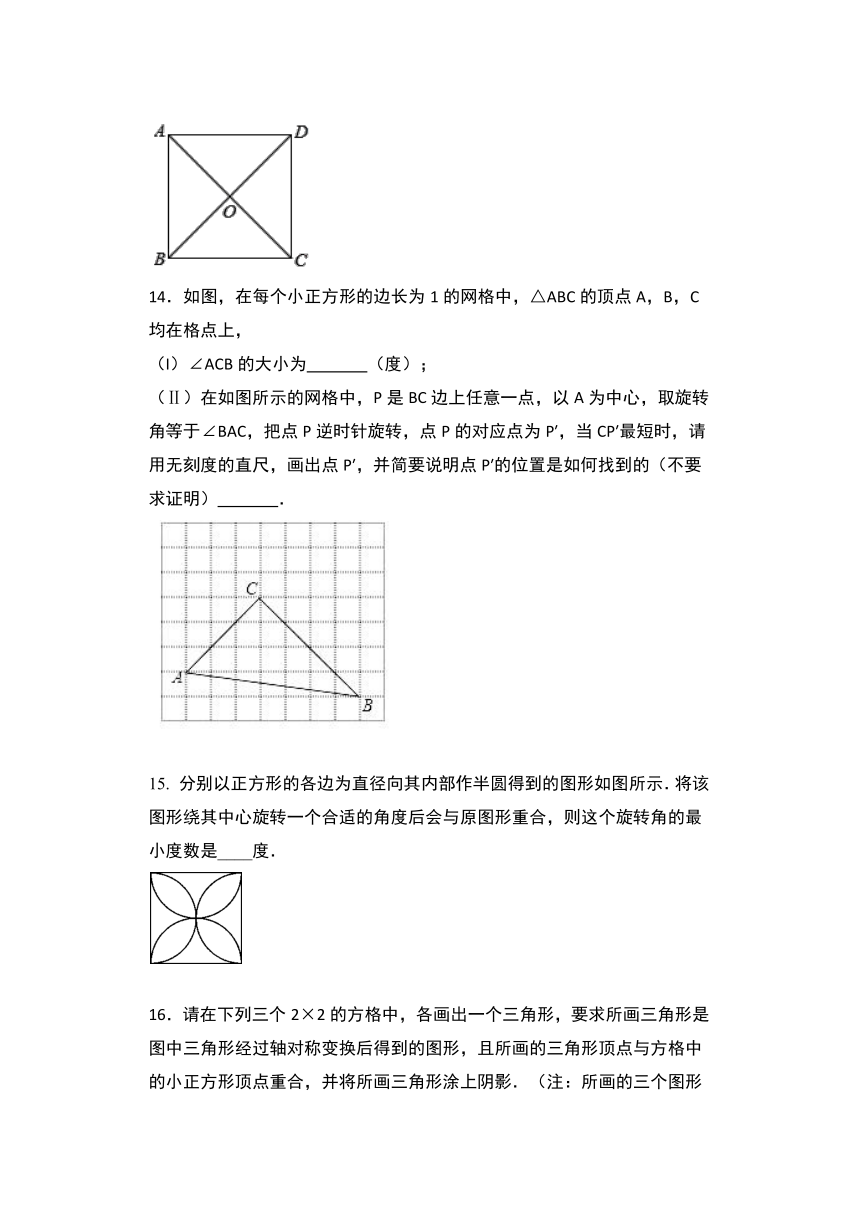
B.右上角梅花,沿对角线平移后,顺时针旋转90°
C.右下角梅花,沿对角线平移后,以下底边为对称轴对称得到的
D.左下角梅花,沿对角线平移后,顺时针旋转90°
9.已知正方形的一条对角线长为2,把正方形经过某种图形变换后的面积为4,则图形变换是( )
A.相似变换
B.旋转变换
C.轴对称变换
D.平移变换
10.如图
,△ABC与△A′B′C′关于点O成中心对称,下列结论不成立的是( )
A.OC=OC′ B.OA=
OA′
C.BC=B′C′
?
D.∠ABC=∠A′C′B′
二、填空题
11.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和________?等。
12.
下列图形均可由“基本图案”变换得到:(只填序号)
(1)平移但不能旋转的是________;
(2)可以旋转但不能平移的是________;
(3)既可以平移,也可以旋转的是________.
13.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
14.如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(I)∠ACB的大小为
(度);
(Ⅱ)在如图所示的网格中,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为P′,当CP′最短时,请用无刻度的直尺,画出点P′,并简要说明点P′的位置是如何找到的(不要求证明)
.
15.
分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是____度.
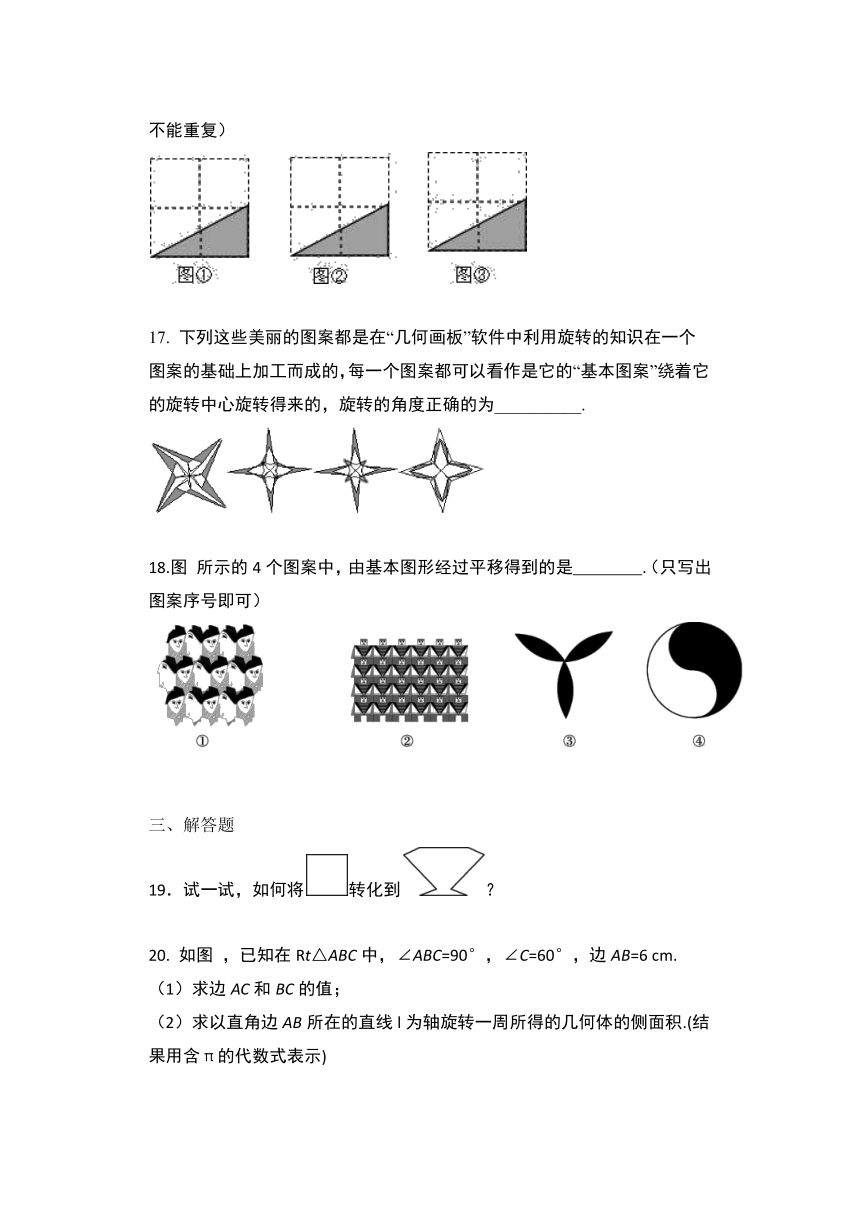
16.请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
17.
下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为__________.
18.图
所示的4个图案中,由基本图形经过平移得到的是 .(只写出图案序号即可)
三、解答题
19.试一试,如何将转化到?
20.
如图
,已知在Rt△ABC中,∠ABC=90°,∠C=60°,边AB=6
cm.
(1)求边AC和BC的值;
(2)求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积.(结果用含π的代数式表示)
21.认真观察图1的4个图中阴影部分构成的图案,回答下列问题:
??????
(1)请写出这四个图案都具有的两个共同特征.
(2)请在图2中设计出你心中的图案,使它也具备你所写出的上述两个特征.
22.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
23.按要求画图:
(1)如图(1)所示,网格内每个小正方形的边长都为1个单位长度,试画出小船向右平移4
个单位长度,向上平移4个单位长度后的图形.
(2)如图(2)过点P分别画直线m、n的垂线.
24.
实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(小于或等于半圆),在图③中重新设计一个不同的轴对称图形.
(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
25.如图所示,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,在平面直角坐标系中,点A的坐标为(﹣2,4).
(1)将△ABC向右平移4个单位与△A1B1C1重合,请在图中作出△A1B1C1;
(2)以原点O为对称中心,画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标:
.
26.
用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
答案
1.
C
2.
B
3.
D
4.
A
5.
B
6.
A
7.
D
8.
D
9.
D
10.
D
11.
旋转
12.
①;②④;③
13.
把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
14.
90°
如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求
15.
90
16.
如图所示:
.
17.
18.
①②
19.
过程如下图:
20.
(1)AC=4
cm,BC=2
cm.?
(2)所求几何体的侧面积S=×(2π·2)×4=24π(cm2)
21.
(1)特征1:是轴对称图形,特征2:是中心对称图形;
(2).
22.
如图(1)所示:将两块四边形拼成正方形,连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,
过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,
∴∠FDA+∠ADE=∠CDE+∠ADE=90°,
∴∠FDA=∠CDE,
在△AFD和△CED中,
,
∴△AFD≌△CED(AAS),
∴FD=DE,
又∵∠B=∠F=∠BED=90°,
∴四边形FBED为正方形.
23.
解:(1)如图(1):
(2)如图(2):a⊥n,b⊥m.
24.
解:答案不唯一,如图
25.
解:(1)如图所示,△A1B1C1即为所求:
(2)如图所示,△A2B2C2即为所求,点C2的坐标(3,﹣1).
故答案为:(3,﹣1).
26.
解:答案不惟一,例如:
一、选择题
1.把一张正方形纸片如图①,图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是(
)
2.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
A.?
B.?
C.?
D.?
3.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.
B.
C.
D.
4.如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )
A.5
B.6
C.4
D.7
5.如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是(
)
6.下列四幅图案在设计中用到平移变换方式的是( )
A.?
B.??
C.?
D.?
7.如图,由图中所示的图案通过平移后得到的图案是( )
A.
B.
C.
D.
8.
观察如图所摆放的五朵梅花,变换中间的一朵梅花,得到四角的梅花,下列说法错误的是(
)
A.左上角梅花,只需沿对角线平移即可
B.右上角梅花,沿对角线平移后,顺时针旋转90°
C.右下角梅花,沿对角线平移后,以下底边为对称轴对称得到的
D.左下角梅花,沿对角线平移后,顺时针旋转90°
9.已知正方形的一条对角线长为2,把正方形经过某种图形变换后的面积为4,则图形变换是( )
A.相似变换
B.旋转变换
C.轴对称变换
D.平移变换
10.如图
,△ABC与△A′B′C′关于点O成中心对称,下列结论不成立的是( )
A.OC=OC′ B.OA=
OA′
C.BC=B′C′
?
D.∠ABC=∠A′C′B′
二、填空题
11.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和________?等。
12.
下列图形均可由“基本图案”变换得到:(只填序号)
(1)平移但不能旋转的是________;
(2)可以旋转但不能平移的是________;
(3)既可以平移,也可以旋转的是________.
13.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
14.如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(I)∠ACB的大小为
(度);
(Ⅱ)在如图所示的网格中,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为P′,当CP′最短时,请用无刻度的直尺,画出点P′,并简要说明点P′的位置是如何找到的(不要求证明)
.
15.
分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是____度.
16.请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
17.
下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为__________.
18.图
所示的4个图案中,由基本图形经过平移得到的是 .(只写出图案序号即可)
三、解答题
19.试一试,如何将转化到?
20.
如图
,已知在Rt△ABC中,∠ABC=90°,∠C=60°,边AB=6
cm.
(1)求边AC和BC的值;
(2)求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积.(结果用含π的代数式表示)
21.认真观察图1的4个图中阴影部分构成的图案,回答下列问题:
??????
(1)请写出这四个图案都具有的两个共同特征.
(2)请在图2中设计出你心中的图案,使它也具备你所写出的上述两个特征.
22.有两块形状完全相同的不规则的四边形木板,如图所示,两位木匠工师傅通过测量可知∠B=∠D=90°,AD=CD,现要将其拼成正方形,思考一段时间后,一位木工师傅说“我可以将这两块木板拼成一个正方形.”另一位木工师傅说“可以将一块木板拼成一个正方形,两块木板拼成两个正方形.”两位师傅把每一块木板都只分割一次,你知道他们是怎么做的吗?画出图形,并说明理由.
23.按要求画图:
(1)如图(1)所示,网格内每个小正方形的边长都为1个单位长度,试画出小船向右平移4
个单位长度,向上平移4个单位长度后的图形.
(2)如图(2)过点P分别画直线m、n的垂线.
24.
实践与操作:如图①是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图②是以图①为基本图案经过图形变换拼成的一个中心对称图形.
(1)请你仿照图①,用两段相等的圆弧(小于或等于半圆),在图③中重新设计一个不同的轴对称图形.
(2)以你在图③中所画的图形为基本图案,经过图形变换在图④中拼成一个中心对称图形.
25.如图所示,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,在平面直角坐标系中,点A的坐标为(﹣2,4).
(1)将△ABC向右平移4个单位与△A1B1C1重合,请在图中作出△A1B1C1;
(2)以原点O为对称中心,画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标:
.
26.
用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
答案
1.
C
2.
B
3.
D
4.
A
5.
B
6.
A
7.
D
8.
D
9.
D
10.
D
11.
旋转
12.
①;②④;③
13.
把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
14.
90°
如图,取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求
15.
90
16.
如图所示:
.
17.
18.
①②
19.
过程如下图:
20.
(1)AC=4
cm,BC=2
cm.?
(2)所求几何体的侧面积S=×(2π·2)×4=24π(cm2)
21.
(1)特征1:是轴对称图形,特征2:是中心对称图形;
(2).
22.
如图(1)所示:将两块四边形拼成正方形,连接BD,将△DBC绕D点顺时针旋转90度,即可得出△B′BD此时三角形是等腰直角三角形,同理可得出正方形B′EBD.如图(2)将一个四边形拼成正方形,
过点D作DE⊥BC于点E,过点D作DF⊥BA交BA的延长线于点F,
∴∠FDA+∠ADE=∠CDE+∠ADE=90°,
∴∠FDA=∠CDE,
在△AFD和△CED中,
,
∴△AFD≌△CED(AAS),
∴FD=DE,
又∵∠B=∠F=∠BED=90°,
∴四边形FBED为正方形.
23.
解:(1)如图(1):
(2)如图(2):a⊥n,b⊥m.
24.
解:答案不唯一,如图
25.
解:(1)如图所示,△A1B1C1即为所求:
(2)如图所示,△A2B2C2即为所求,点C2的坐标(3,﹣1).
故答案为:(3,﹣1).
26.
解:答案不惟一,例如:
同课章节目录
